Содержание
- Обозначение геометрических фигур буквами
- Точка
- Отрезок
- Ломаная линия
- Многоугольники
- Угол
- Обозначения и символика
- Основы геометрии
- Точка
- Прямая
- Способы обозначения прямых
- Способы обозначения лучей
- Отрезок
- Ломаная
- Плоскость, прямая линия, луч
- Прямая линия
- Обозначение прямой
- Некоторые свойства прямой
- Обозначение луча
- Углы в геометрии
- Способы обозначения углов
- Виды углов
Обозначение геометрических фигур буквами
В математике есть правило: обозначать геометрические фигуры заглавными буквами латинского алфавита. Сегодня мы научимся этому.
Точка
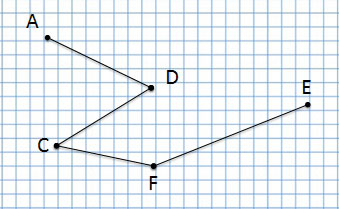
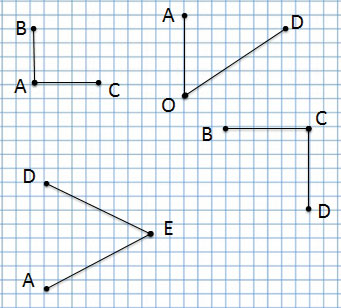
точка А, точка С, точка D, точка Е и точка F.
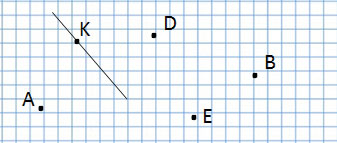
Отрезок
отрезок AD, отрезок СВ, отрезок FE
Сколько всего отрезков на данном чертеже?
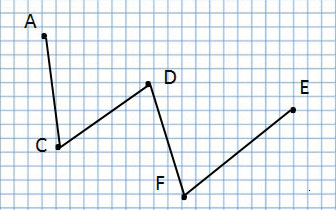
Ломаная линия
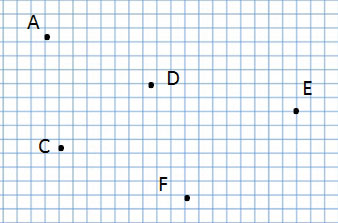
А эта ломаная линия совсем по-другому, потому что соединение точек у неё другое:
Ломаная линия ACDFE
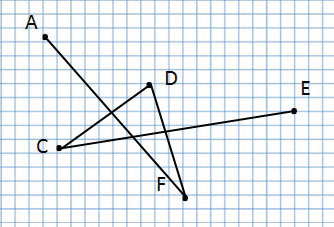
Прочитаю название следующей ломаной линии:
Ломаная линия AFDCE
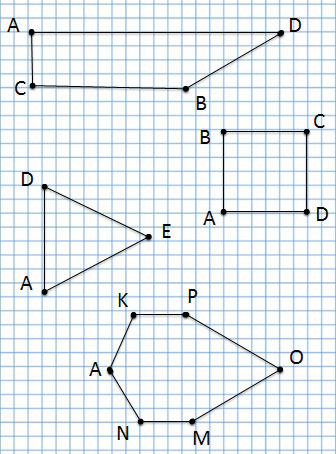
Многоугольники
Угол
Угол обозначается тремя буквами. В середине указывается буква, которая обозначает вершину угла.
1 угол: угол BAC или CAB с вершиной А
2 угол: угол AOD или DOA с вершиной О
3 угол: угол AED или DEA с вершиной Е
4 угол: угол BCD или DCB с вершиной С
Поделись с друзьями в социальных сетях:
Источник
Обозначения и символика
Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).
Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:
группа I — обозначения геометрических фигур и отношений между ними;
группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.
Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.
СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ
А. Обозначение геометрических фигур
1. Геометрическая фигура обозначается — Ф.
2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:
3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:
Линии уровня обозначаются: h — горизонталь; f— фронталь.
Для прямых используются также следующие обозначения:
(АВ) — прямая, проходящая через точки А а В;
[АВ) — луч с началом в точке А;
[АВ] — отрезок прямой, ограниченный точками А и В.
4. Поверхности обозначаются строчными буквами греческого алфавита:
Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:
α(а || b) — плоскость α определяется параллельными прямыми а и b;
5. Углы обозначаются:
6. Угловая: величина (градусная мера) обозначается знаком 


Прямой угол отмечается квадратом с точкой внутри
7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.
|АВ| — расстояние между точками А и В (длина отрезка АВ);
|Аа| — расстояние от точки А до линии a;
|Аα| — расстояшие от точки А до поверхности α;
|аb| — расстояние между линиями а и b;
|αβ| расстояние между поверхностями α и β.
π2 —фрюнтальная плоскость проекций.
При замене плоскостей проекций или введении новых плоскостей последние обозначают π3, π4 и т. д.
Постояшную прямую эпюра Монжа обозначают k.
10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:
11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса 0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.
12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.
Например: Ha — горизонтальный след прямой (линии) а;
Fa — фронтальный след прямой (линии ) a.
13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами 1,2,3. n:
Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом 0:
14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0 :
15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :
Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.
Источник
Основы геометрии
Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.
Познакомимся с основными геометрическими понятиями, изучаемыми в начальной школе.
Точка
Точка — это основная и самая простая геометрическая фигура.
В геометрии точка обозначается заглавной латинской буквой или цифрой. Многие латинские буквы по написанию похожи на английские буквы.
В тексте точку обозначают следующим символом: « (·) A » — точка « А ».
Прямая
Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.
Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.
Способы обозначения прямых
Способы обозначения лучей
Отрезок
Основное свойство отрезка — это его длина.
Длина отрезка — это расстояние между его концами.
В математике отрезок обозначается заглавными латинскими буквами.
Ломаная
Ломаная — это геометрическая фигура, состоящая из точек, которые соединены отрезками.
Вершины ломаной — это точки, в которых соединяются отрезки, образующие ломаную.
Звенья ломаной — это отрезки ломаной.
В математике ломаная обозначается заглавными латинскими буквами.
Чтобы найти длину ломаной, необходимо сложить длины всех её звеньев (отрезков), из которых она состоит.
KLCM = KL + LC + CM = 3 см + 2 см + 2 см = 7 см
Вот мы и познакомились с основами геометрии. Теперь мы готовы рассмотреть не менее важную геометрическую фигуру — угол.
Источник
Плоскость, прямая линия, луч
Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.
Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.
Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.
Плоскость нельзя измерять, потому что она бесконечная.
Плоскость нельзя согнуть, в каком бы положении она ни находилась.
Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.
Прямая линия
Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.
Обозначение прямой
Например, на рисунке 1 обозначены такие прямые:
Рис. 1 Обозначение прямой линии
Рис. 2 Обозначение прямой с несколькими точками
Некоторые свойства прямой
Две точки, лежащие на одной прямой, создают отрезок этой прямой.
Через две любые точки на плоскости можно провести единственную прямую.
Рис. 3 Отрезок на прямой
Две разные прямые могут пересекаться или не пересекаться.
Две прямые пересекаются в том случае, если у них есть общая точка.
Рис. 5 Пересечение прямых
Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.
Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.
Рис. 6 Деление прямой линии точкой
У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.
Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.
Обозначение луча
Луч, как и прямую, обозначают двумя способами.
Рис. 7 Обозначение луча
На рисунке 2 приведены примеры обозначения луча:
Луч имеет второе название – полупрямая.
Рис. 8 Дополнительные друг другу и совпадающие лучи
На рисунке 8 видно, что:
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.6 / 5. Количество оценок: 18
Источник
Углы в геометрии
Угол — это геометрическая фигура, которая состоит из двух лучей и вершины.
Вершина угла — это точка, в которой два луча берут начало.
Стороны угла — это лучи, которые образуют угол.
Например: 
Стороны угла — « OA » и « OB ».
Для обозначения угла в тексте используется символ: 
Способы обозначения углов
Одной заглавной латинской буквой, указывающей его вершину.


Тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.


Называть угол можно с любого края, но НЕ с вершины.
При таком обозначении вершина угла должна всегда находиться в середине названия.
Единица измерения углов — градусы. Углы измеряют с помощью специального прибора — транспортира.
Для обозначения градусов в тексте используется символ: °
50 градусов обозначаются так: « 50° »
Виды углов
| Вид угла | Размер в градусах | Пример |
|---|---|---|
| Прямой | Равен 90° |  |
| Острый | Меньше 90° |  |
| Тупой | Больше 90° |  |
| Развернутый | Равен 180° |  |
Два угла могут иметь одну общую сторону.
Обратите внимание на рисунок ниже. Попробуйте сосчитать и назвать все углы на изображении.
Если насчитали три угла, то вы правы. Давайте их назовём:
Источник
B = {9,14,28}
B = {3,9,14},
A = B
B = {1,2,3},
AB = {9,14}
B = {1,2,3},
AB = {9,14}
B = {1,2,3},
A ∆ B = {1,2,9,14}
B = {1,2,3},
A ⊖ B = {1,2,9,14}
принадлежит
В разделе собраны математические символы, которые невозможно корректно отобразить с помощью ввода на клавиатуре. Весь представленный набор можно разделить на несколько групп:
- знаки операций – сложение, вычитание, деление, умножение, сумма;
- символы интегралов – двойные, тройные, интеграл по объему, поверхности, с правым и левым обходом;
- знаки сравнения – больше, меньше;
- примерно равно, не равно, эквивалентно, тождественно;
- геометрические символы – отображение угла, пропорции, диаметра, перпендикуляра, параллельности, пересечения;
- геометрические фигуры — треугольники, дуги, параллелограмм, ромб;
- знак извлечения из корня, степень числа;
- для теории множеств — пустое множество, принадлежит, подмножество, объединение, пересечение;
- логические — следовательно, и, или, отрицание, равносильно;
- иные символы – бесконечность, существует, принадлежит, оператор набла, троеточия для матриц, скобки потолков числа, для теории групп.
Примеры использования
Функция параболы: ƒ(x)=ax²+bx+c (a≠0)
Определение исключающего «ИЛИ»: A⊕B :⇔ (A⋁B) ∧¬ (A∧B)
Скорость, с которой упадет тело с высоты h: V=√̅2̅g̅h̅
Использование данных иконок – единственный вариант корректного отображения ряда математических символов на сайте или в сообщении в любой операционной системе конечного пользователя. Достаточно лишь скопировать закодированный значок. Применение изображений для этих целей значительно усложняет процесс, требует подгонки при разработке и наполнении интернет-ресурса. Кроме того, медиа-контент занимает большой объем дискового пространства.
Математические символы подойдут для публикаций в социальных сетях, создания сообщений в чатах и форумах, разработки интернет-страниц.
Математика, как язык всех наук, не может обходиться без системы записи. Многочисленные понятия, и операторы обрели своё начертание по мере развития этой науки. Так как в стандартные алфавиты эти символы не входят, напечатать их с клавиатуры может оказаться проблематично. Отсюда можно скопировать и вставить.
Консорциум Юникода включил в таблицу множество различных знаков. Если тут нет того, что нужно, воспользуйтесь поиском по сайту или посмотрите в разделах:
Математические операторы 2200–22FF
Разные математические символы — A 27C0–27EF
Разные математические символы — B 2980–29FF
Дополнительные математические операторы 2A00–2AFF
Буквы для формул:
Греческое и коптское письмо 0370–03FF
Математические буквы и цифры 1D400–1D7FF
Степени и дроби
Для степеней числа используются Подстрочные и надстрочные цифры. Мы собрали их в отдельный набор. В этом же наборе собраны дроби.
Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).
Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:
группа I — обозначения геометрических фигур и отношений между ними;
группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.
Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.
Группа I
СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ
А. Обозначение геометрических фигур
1. Геометрическая фигура обозначается — Ф.
2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:
А, В, С, D, … , L, М, N, …
1,2,3,4,…,12,13,14,…
3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:
а, b, с, d, … , l, m, n, …
Линии уровня обозначаются: h — горизонталь; f— фронталь.
Для прямых используются также следующие обозначения:
(АВ) — прямая, проходящая через точки А а В;
[АВ) — луч с началом в точке А;
[АВ] — отрезок прямой, ограниченный точками А и В.
4. Поверхности обозначаются строчными буквами греческого алфавита:
α, β, γ, δ,…,ζ,η,ν,…
Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:
α(а || b) — плоскость α определяется параллельными прямыми а и b;
β(d1 d2gα) — поверхность β определяется направляющими d1 и d2 , образующей g и плоскостью параллелизма α.
5. Углы обозначаются:
∠ABC — угол с вершиной в точке В, а также ∠α°, ∠β°, … , ∠φ°, …
6. Угловая: величина (градусная мера) обозначается знаком 


Прямой угол отмечается квадратом с точкой внутри
7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.
Например:
|АВ| — расстояние между точками А и В (длина отрезка АВ);
|Аа| — расстояние от точки А до линии a;
|Аα| — расстояшие от точки А до поверхности α;
|аb| — расстояние между линиями а и b;
|αβ| расстояние между поверхностями α и β.
8. Для плоскостей проекций приняты обозначения: π1 и π2,
где π1 — горизонтальная плоскость проекций;
π2 —фрюнтальная плоскость проекций.
При замене плоскостей проекций или введении новых плоскостей последние обозначают π3, π4 и т. д.
9. Оси проекций обозначаются: х, у, z, где х — ось абсцисс; у — ось ординат; z — ось аппликат.
Постояшную прямую эпюра Монжа обозначают k.
10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:
А’, В’, С’, D’, … , L’, М’, N’, горизонтальные проекции точек; А», В», С», D», … , L», М», N», … фронтальные проекции точек; a’ , b’ , c’ , d’ , … , l’, m’ , n’ , —
горизонтальные проекции линий; а» ,b» , с» , d» , … , l» , m» , n» , … фронтальные проекции линий; α’, β’, γ’, δ’,…,ζ’,η’,ν’,… горизонтальные проекции поверхностей;
α», β», γ», δ»,…,ζ»,η»,ν»,…
фронтальные проекции поверхностей.
11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса 0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.
Так: h0α — горизонтальный след плоскости (поверхности) α;
f0α — фронтальный след плоскости (поверхности) α.
12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.
Например: Ha — горизонтальный след прямой (линии) а;
Fa — фронтальный след прямой (линии ) a.
13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами 1,2,3,…, n:
А1, А2, А3,…,Аn;
a1, a2, a3,…,an;
α1, α2, α3,…,αn;
Ф1, Ф2, Ф3,…,Фn и т. д.
Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом 0:
A0, B0, С0, D0, …
Аксонометрические проекции
14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0:
А0, В0, С0, D0, …
10, 20, 30, 40, …
a0, b0, c0, d0, …
α0, β0, γ0, δ0, …
15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :
А1 0, В1 0, С1 0, D1 0, …
11 0, 21 0, 31 0, 41 0, …
a1 0, b1 0, c1 0, d1 0, …
α1 0, β1 0, γ1 0, δ1 0, …
Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.
| № по пор. | Обозначение | Содержание | Пример символической записи |
|---|---|---|---|
| 1 | ≡ | Совпадают | (АВ)≡(CD) — прямая, проходящая через точки А и В, совпадает с прямой, проходящей через точки С и D |
| 2 | ≅ | Конгруентны | ∠ABC≅∠MNK — угол АВС конгруентен углу MNK |
| 3 | ∼ | Подобны | ΔАВС∼ΔMNK — треугольники АВС и MNK подобны |
| 4 | || | Параллельны | α||β — плоскость α параллельна плоскости β |
| 5 | ⊥ | Перпендикулярны | а⊥b — прямые а и b перпендикулярны |
| 6 |  |
Скрещиваются | с  d — прямые с и d скрещиваются d — прямые с и d скрещиваются |
| 7 |  |
Касательные | t  l — прямая t является касательной к линии l. l — прямая t является касательной к линии l. β  α — плоскость β касательная к поверхности α α — плоскость β касательная к поверхности α |
| 8 | → | Отображаются | Ф1→Ф2 — фигура Ф1 отображается на фигуру Ф2 |
| 9 | S | Центр проецирования. Если центр проецирования несобственная точка, то его положение обозначается стрелкой, указывающей направление проецирования |
— |
| 10 | s | Направление проецирования | — |
| 11 | P | Параллельное проецирование | рsα Параллельное проецирование — параллельное проецирование на плоскость α в направлении s |
| № по пор. | Обозначение | Содержание | Пример символической записи | Пример символической записи в геометрии |
|---|---|---|---|---|
| 1 | M,N | Множества | — | — |
| 2 | A,B,C,… | Элементы множества |
— | — |
| 3 | { … } | Состоит из … | Ф{A, B, C,… } | Ф{A, B, C,… } — фигура Ф состоит из точек А, В,С, … |
| 4 | ∅ | Пустое множество | L — ∅ — множество L пустое (не содержит элементов ) | — |
| 5 | ∈ | Принадлежит, является элементом | 2∈N (где N — множество натуральных чисел) — число 2 принадлежит множеству N |
А ∈ а — точка А принадлежит прямой а (точка А лежит на прямой а ) |
| 6 | ⊂ | Включает, cодержит | N⊂М — множество N является частью (подмножеством) множества М всех рациональных чисел |
а⊂α — прямая а принадлежит плоскости α (понимается в смысле: множество точек прямой а является подмножеством точек плоскости α) |
| 7 | ∪ | Объединение | С = A U В — множество С есть объединение множеств A и В; {1, 2. 3, 4,5} = {1,2,3}∪{4,5} |
ABCD = [AB] ∪ [ВС] ∪ [CD] — ломаная линия, ABCD есть объединение отрезков [АВ], [ВС], [CD] |
| 8 | ∩ | Пересечение множеств | М=К∩L — множество М есть пересечение множеств К и L (содержит в себе элементы, принадлежащие как множеству К, так и множеству L). М ∩ N = ∅— пересечение множеств М и N есть пустое множество (множества М и N не имеют общих элементов) |
а = α ∩ β — прямая а есть пересечение плоскостей α и β а ∩ b = ∅ — прямые а и b не пересекаются (не имеют общих точек) |
| № по пор. | Обозначение | Содержание | Пример символической записи |
|---|---|---|---|
| 1 | ∧ | Конъюнкция предложений; соответствует союзу «и». Предложение (р∧q) истинно тогда и только тогда,когда р и q оба истинны |
α∩β = { К:K∈α∧K∈β} Пересечение поверхностей α и β есть множество точек (линия), состоящее из всех тех и только тех точек К, которые принадлежат как поверхности α, так и поверхности β |
| 2 | ∨ | Дизъюнкция предложений; соответствует союзу «или». Предложение (p∨q) истинно, когда истинно хотя бы одно из предложений р или q (т. е. или р, или q, или оба). |
— |
| 3 | ⇒ | Импликация — логическое следствие. Предложение р⇒q означает: «если р, то и q» | (а||с∧b||с)⇒a||b. Если две прямые параллельны третьей, то они параллельны между собой |
| 4 | ⇔ | Предложение (р⇔q) понимается в смысле: «если р, то и q; если q, то и р» | А∈α⇔А∈l⊂α. Точка принадлежит плоскости, если она принадлежит некоторой линии, принадлежащей этой плоскости. Справедливо также и обратное утверждение: если точка принадлежит некоторой линии, принадлежащей плоскости, то она принадлежит и самой плоскости |
| 5 | ∀ | Квантор общности, читается: для всякого, для всех, для любого. Выражение ∀(x)P(x) означает: «для всякого x: имеет место свойство Р(х) « |
∀( ΔАВС)(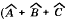 = 180°) Для всякого (для любого) треугольника сумма величин его углов = 180°) Для всякого (для любого) треугольника сумма величин его углов при вершинах равна 180° |
| 6 | ∃ | Квантор существования, читается: существует. Выражение ∃(х)P(х) означает: «существует х, обладающее свойством Р(х)» |
(∀α)(∃a)[a⊄α∧a||α].Для любой плоскости α существует прямая а, не принадлежащая плоскости α и параллельная плоскости α |
| 7 | ∃1 | Квантор единственности существования, читается: существует единственное (-я, -й)… Выражение ∃1(x)(Рх) означает: «существует единственное (только одно) х, обладающее свойством Рх» |
(∀ А, В)(А≠B)(∃1а)(а∋А, В) Для любых двух различных точек А и В существует единственная прямая a, проходящая через эти точки. |
| 8 | (Px) | Отрицание высказывания P(x) | а b(∃α)(α⊃а, Ь).Если прямые а и b скрещиваются, то не существует плоскости а, которая содержит их b(∃α)(α⊃а, Ь).Если прямые а и b скрещиваются, то не существует плоскости а, которая содержит их |
| 9 | Отрицание знака | [AB]≠[CD] —отрезок [АВ] не равен отрезку [CD].а?b — линия а не параллельна линии b |
,,э,, только в другую сторону
Ниже представлена таблица с основными математическими символами и знаками, которые используются в геометрии с 7 класса и старше.
| Знак | Название | Значение/описание | Пример |
| ∠ | угол | фигура, состоящая из двух лучей и вершины | ∠ABC = 30° |
| острый угол | угол от 0 до 90 градусов | ∠AOB = 60° | |
| прямой угол | угол, равный 90 граусам | ∠AOB = 90° | |
| тупой угол | угол от 90 до 180 градусов | ∠AOB = 120° | |
 |
развернутый угол | угол, равный 180 градусам | ∠AOB = 180° |
| ° (или deg) |
градус | единица измерения угла, равна 1/360 окружности | 45° |
| ′ | минута | единица измерения угла, 1° = 60′ | α = 70°59′ |
| ″ | секунда | единица измерения угла, 1′ = 60″ | α = 70°59′59″ |
| линия | бесконечная прямая без начала и конца | ||
| отрезок | участок на прямой между точками A и B | ||
| луч | бесконечная прямая, имеющая начало в точке A, но не имеющая конца | ||
| дуга | дуга, образованная между точками A и B | ||
| ⊥ | перпендикулярность | линии (прямые), расположенные под углом 90° по отношению друг к другу | AC ⊥ BC |
| || | параллельность | непересекающиеся прямые (линии) | AB || CD |
| ∩ | пересечение | множество одинаковых элементов, принадлежащих как множеству A, так и B | A ∩ B |
| ∈ / ∉ | принадлежность/ непринадлежность |
элемент является/не является элементом заданного множества | a ∈ S |
| ≅ | конгуэнтность | эквивалентность геометрических форм и размеров | ∆ABC ≅ ∆XYZ |
| ~ | подобие | та же форма, но разные размеры | ∆ABC ~ ∆XYZ |
| Δ | треугольник | фигура треугольника | ΔABC ≅ ΔBCD |
| |x-y| | дистанция | дистанция между точками X и Y | | x-y | = 5 |
| π | константа «Пи» | отношение длины окружности к диаметру круга, π = C/d | π = 3.141592654… |
| рад (rad) или c |
радиан | единица измерения угла | 360° = 2π c |
microexcel.ru
Сомневаетесь в ответе?
Найдите правильный ответ на вопрос ✅ «Как в геометрии пишется знак принадлежности? …» по предмету 📘 Геометрия, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Аня Колесникова
Ученик
(222),
закрыт
10 лет назад
Лучший ответ
Maxim
Гений
(71098)
10 лет назад
Этот знак используется не только в геометрии и изображается ∩
Остальные ответы
РОМАН ВОРОНЦОВ
Профи
(759)
10 лет назад
∩ знак пересечения
Мери теккозян
Ученик
(136)
6 лет назад
∩ знак
Хо Минхо
Профи
(690)
5 лет назад
∩ — знак пересечения
Мария Стасевич
Ученик
(135)
3 года назад
Перевёрнутая U
Некто никто
Профи
(543)
3 года назад
Этот знак используется не только в геометрии и обозначается ∩
Ҝρนĉ⍡นӈα
Гуру
(3130)
3 года назад
∩
Mihail Dogadov
Ученик
(112)
1 год назад
∩
13
1 ответ:
0
0
Мне кажется так,просто я ещё не изучаю геометрию.
Читайте также
жалко не могу скинуть фотку.
так что на словах: биссектрис-т.е угол по 45град значит катеты равны по 2 см
гипотенузу найти по т.пифагора. 2под корнем 2
периметр: 4+2под корнем 2
Задача имеет два случая, но , что интересно, единственное решение. Значит, случай все же один. Но все равно будем считать как два, т.к рисунков «типа два»
Решение в файле.
44ЕВ будет примерно в Сталинграде
П4=10
В тр-ке ABC: AC=CB=10см, угол а=30 градусов, BK- перпендикуляр у плоскости треугольника и равен 5 см найти расстояние от K до AC
рассмотрим образованную пирамиду АВСК, КВ перпендикулярно АВС, значит нам необходимо найти длину высоты, опущенной в грани АСК из вершины К на АС, По теореме о трех перпендикулярах ее проекция на плоскость АВС будет перпендикулярна АС. Обозначим точку пересечения высоты с АС через Н. Тогда нужно найти КН.
рассмотрим основание пирамиды — треугольник АВС, Он равнобедренный ас=ВС=10 с углом у основания А=30 градусов. Опустим высоту из вершины треугольника С на АВ — СМ. Высота, опущенная из точки С, будет и биссектрисой, и медианой треугольника. То есть АМ=МВ. Треугольник АСМ — прямоугольный, с одним из осмтрых углов = 30 градусов, значит катет, лежащий против этого угла, равен половине гипотенузы: АМ=1/2*АС, АМ=1/2*10=5 (см). По теореме Пифагора найдем второй катет СМ:
CM=sqrt(AC2-AM2)
CM=sqrt(100-25)=sqrt75=5sqrt3
BH- проекция КН на плоскость основания АВС, и, как было уже отмечено, ВН перпендикулярна АС. Рассм отрим треугольники АНВ и АМС- они подобны:
АН/АМ=НВ/МС=АВ/АС
НВ/МС=АВ/АС
НВ=МС*АВ/АС
НВ=5*(2*5sqrt3)/10=5sqrt3
Треугольник КНВ — прямоугольный (КВ перпендикулярно плоскости АВС). По теореме Пифагора найдем КН:
KH2=KB2+HB2
KH=sqrt(25+75)=sqrt100=10 (см)
Площадь параллелограма можно найти по формуле S= ABумножить наВС и на sinуглаВ. S=16*40*sin150. sin150=sin30=1/2. S=320
Страницы работы
Содержание работы
Чесноков Е. А.
МАТЕМАТИЧЕСКИЙ АНАЛИЗ ФУНКЦИИ
ОДНОЙ ПЕРЕМЕННОЙ
Северо – Западная академия государственной службы
Санкт – Петербург, 2008
Введение
Настоящее учебное пособие посвящено …
1. Сокращенные обозначения в математике
В математической литературе используются ряд символов (знаков), призванных
сократить запись наиболее часто встречающихся в математике предложений.
Использование математических символов позволяет значительно ускорить процесс
конспектирования, а также существенно сократить время записи решения задач.
Приведем некоторые наиболее часто встречающиеся символы:
 — знак принадлежности:
— знак принадлежности: означает, что элемент
означает, что элемент  принадлежит множеству
принадлежит множеству 
— знак подмножества:
означает, что множество
является подмножеством (составной частью)
множества , иначе говоря все элементы, принадлежащие
, принадлежат также и
— знак допущения, заменяет слова
«предположим», «допустим»
— знак существования, как
правило заменяет слово «существует»
— знак произвольности, обычно
заменяет слово «любой»
— знак единственности,
используется вместо слова «единственный»
— знак окрестности (некоторой
прилегающей области)
— знак следствия:
означает, что из утверждения
следует утверждение
, то есть при выполнении
обязательно будет выполняться и
— знак эквивалентности:
означает, что утверждения
и
эквивалентны
(равнозначны), то есть и
выполняются
или не выполняются одновременно
— знак тождественного равенства:
например, подчеркивает, что равенство имеет место
при всех , в то время как уравнение
выполняется только при
— знак приближенного (неточного)
равенства
— знак рассмотрения (глаз),
заменяет слово «рассмотрим»
— знак, заменяющий слова «такое,
что»
Перечеркнутый символ означает отрицание, например:
— «не равно»
— «не принадлежит»
Пример 1: Предложение «допустим, что существует единственное решение уравнения » можно коротко записать как «
»
Пример 2: Предложение «рассмотрим некоторую окрестность точки , такую, что для любого
, принадлежащего этой окрестности,
выполняется неравенство » эквивалентно записи «
».
2. Элементы математической логики
Доказательства различных математических утверждений в конечном счете
основываются на логических связях между некоторыми высказываниями, каждое из
которых может быть оценено как истинное или ложное. По сути дела,
доказательство некоторого неочевидного утверждения сводится к тому, что это
утверждение раскладывается в цепь логически связанных элементарных
высказываний, каждое из которых без труда может быть оценено как истинное или
ложное. Один раз тщательно проверенная логическая цепь может использоваться в
дальнейшем (например, в виде теоремы) как составная часть более длинной цепи,
соответствующей некоторому более сложному утверждению. В качестве примера
рассмотрим два наиболее часто встречающихся способа математических
доказательств: доказательство от противного и метод математической индукции.
Определение 1: Утверждение, состоящее в том, что утверждение ложно (
не
имеет места), называют отрицанием и обозначают
. Отметим, что
.
Определение 2: Логическим сложением утверждений (
)
называют утверждение, состоящее в том, что по крайней мере одно из двух
утверждений ( или
) истинно.
Определение 3: Логическим умножением утверждений (
)
называют утверждение, состоящее в том, что оба утверждения ( и
)
истинны.
Определение 4: Импликацией (логическим следствием) называют утверждение, состоящее в том, что
если утверждение истинно, то и утверждение
тоже истинно (если
ложно,
то импликация считается истинной), называют условием,
— заключением.
Определение 5: Утверждения и
называют взаимно обратными.
Определение 6: Произведение прямого и обратного утверждений называют утверждением эквивалентности
и обозначают . Утверждение эквивалентности означает, что
либо и
оба
истинны, либо они оба ложны, при этом не имеет значения какое из двух
утверждений делать.
Определение 7: Утверждения и
называют взаимно противоположными.
Теорема 1:
И то и другое утверждения являются ложными только
в одном случае: когда — истинное, а
— ложное, в остальных случаях оба
утверждения истинны. Ч.Т.Д.
Теорема 2: Прямое и противоположное обратному утверждения эквивалентны
(равносильны):
Действительно, из Т1 следует: Ч.Т.Д.
На непосредственном использовании Т2 основан
способ доказательства, который носит название доказательства от противного:
делается предположение, которое отрицает следствие импликации (теоремы), после
чего показывается, что данное предположение приводит к отрицанию условия
импликации, то есть к логическому противоречию, откуда следует вывод об
истинности следствия импликации. Другими словами, вместо прямого утверждения доказывается утверждение противоположное
обратному .
Пример 1: Докажем, что число иррациональное, то есть
не может быть представлено в виде несократимой дроби .
Условие теоремы: (
— несократимая дробь, то есть натуральные
числа и
не
содержат в своем составе общих простых чисел).
Следствие теоремы:
Предположим, что следствие теоремы ложно:
Похожие материалы
- Математический анализ функции одной переменной: Учебное пособие. Часть 2 (Производные высших порядков. Ряд Тейлора. Раскрытие неопределенностей. Сходимость ряда Тейлора. Ряд Лорана)
- Определение степени с дробным показателем. Область определения неравенства
- Комбинированные уравнения. Указания для решения контрольных тестов
Информация о работе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Навигация по справочнику TehTab.ru: 
|
Таблица математических символов. Сокращённая запись математического текста, математические обозначения. Математический алфавит. Математическая скоропись. Негламурный эксклюзив от Проекта DPVA.info
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

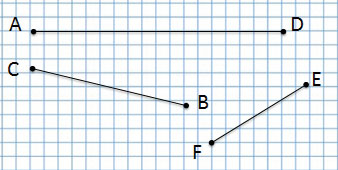





















 — матрица того же размера, элементы которой равны произведению соответствующих элементов перемножаемых матриц
— матрица того же размера, элементы которой равны произведению соответствующих элементов перемножаемых матриц 







 , где m≥0; ak — целые числа, а p — простое число.
, где m≥0; ak — целые числа, а p — простое число.











 x
x — это наибольшее целое число, меньшее или равное х.
— это наибольшее целое число, меньшее или равное х.
 x
x -это наименьшее целое число, большее или равное х.
-это наименьшее целое число, большее или равное х.
































 =vx i +vy j +vz k , где vx, vy, vz — функции от трех переменных x, y, z, а i, j, k — стандартный базис в пространстве, то
=vx i +vy j +vz k , где vx, vy, vz — функции от трех переменных x, y, z, а i, j, k — стандартный базис в пространстве, то




 — граница множества M (другими словами, множество всех граничных точек множества M)
— граница множества M (другими словами, множество всех граничных точек множества M) — степень многочлена f. Чаще встречается обозначение deg f.
— степень многочлена f. Чаще встречается обозначение deg f.







 ,
,  .
.








 — алгебраическое замыкание поля T, т.е. алгебраически замкнутое расширение поля T. Поле называется алгебраически замкнутым, если каждый многочлен ненулевой степени над этим полем имеет хотя бы 1 корень.
— алгебраическое замыкание поля T, т.е. алгебраически замкнутое расширение поля T. Поле называется алгебраически замкнутым, если каждый многочлен ненулевой степени над этим полем имеет хотя бы 1 корень. — топологическое замыкание подмножества S, т.е. пересечение всех замкнутых надмножеств подмножества S.
— топологическое замыкание подмножества S, т.е. пересечение всех замкнутых надмножеств подмножества S.

 — строгое, истинное подмножество
— строгое, истинное подмножество

