Скачать: |pdf| |doc| |epub| |fb2| |иллюстрации|
ВВЕДЕНИЕ
ЗОЛОТОЕ СЕЧЕНИЕ — ГАРМОНИЧЕСКАЯ ПРОПОРЦИЯ
ВТОРОЕ ЗОЛОТОЕ СЕЧЕНИЕ
ЗОЛОТОЙ ТРЕУГОЛЬНИК (пентаграмма)
ИСТОРИЯ ЗОЛОТОГО СЕЧЕНИЯ
ИКОСАЭДР И ДОДЕКАЭДР
ЗОЛОТОЕ СЕЧЕНИЕ И СИММЕТРИЯ
РЯД ФИБОНАЧЧИ
ОБОБЩЁННОЕ ЗОЛОТОЕ СЕЧЕНИЕ
ПРИНЦИПЫ ФОРМООБРАЗОВАНИЯ В ПРИРОДЕ
ТЕЛО ЧЕЛОВЕКА И ЗОЛОТОЕ СЕЧЕНИЕ
ЗОЛОТОЕ СЕЧЕНИЕ В СКУЛЬПТУРЕ
ЗОЛОТОЕ СЕЧЕНИЕ В АРХИТЕКТУРЕ
ЗОЛОТОЕ СЕЧЕНИЕ В МУЗЫКЕ
ЗОЛОТОЕ СЕЧЕНИЕ В ПОЭЗИИ
ЗОЛОТОЕ СЕЧЕНИЕ В ШРИФТАХ И БЫТОВЫХ ПРЕДМЕТАХ
ОПТИМАЛЬНЫЕ ФИЗИЧЕСКИЕ ПАРАМЕТРЫ ВНЕШНЕЙ СРЕДЫ
ЗОЛОТОЕ СЕЧЕНИЕ В ЖИВОПИСИ
ЗОЛОТОЕ СЕЧЕНИЕ И ВОСПРИЯТИЕ ИЗОБРАЖЕНИЯ
ЗОЛОТОЕ СЕЧЕНИЕ В ФОТОГРАФИИ
ЗОЛОТОЕ СЕЧЕНИЕ И КОСМОС
ЗАКЛЮЧЕНИЕ
ВВЕДЕНИЕ
Людей с давних времён волновал вопрос, подчиняются ли такие неуловимые вещи как красота и гармония каким-либо математическим расчётам. Конечно, все законы красоты невозможно вместить в несколько формул, но, изучая математику, мы можем открыть некоторые слагаемые прекрасного — золотое сечение. Наша задача — узнать что же такое золотое сечение и установить — где человечество нашло применение золотого сечения.
Вы, наверное, обращали внимание, что мы неодинаково относимся к предметам и явлениям окружающей действительности. Безпорядочность, безформенность, несоразмерность воспринимаются нами как безобразное и производят отталкивающее впечатление. А предметы и явления, которым свойственна мера, целесообразность и гармония, воспринимаются как красивое и вызывают у нас чувство восхищения, радости, поднимают настроение.
Человек в своей деятельности постоянно сталкивается с предметами, имеющими в своей основе золотое сечение. Есть вещи, которые нельзя объяснить. Вот вы подходите к пустой скамейке и садитесь на нее. Где вы сядете? Посередине? Или, может быть, с самого края? Нет, скорее всего, не то и не другое. Вы сядете так, что отношение одной части скамейки к другой относительно вашего тела будет равно примерно 1,62. Простая вещь, абсолютно инстинктивная… Садясь на скамейку, вы воспроизвели «золотое сечение».
О золотом сечении знали еще в древнем Египте и Вавилоне, в Индии и Китае. Великий Пифагор создал тайную школу, где изучалась мистическая суть «золотого сечения». Евклид применил его, создавая свою геометрию, а Фидий — свои бессмертные скульптуры. Платон рассказывал, что Вселенная устроена согласно «золотому сечению». Аристотель нашел соответствие «золотого сечения» этическому закону. Высшую гармонию «золотого сечения» будут проповедовать Леонардо да Винчи и Микеланджело, ведь красота и «золотое сечение» — это одно и то же. А христианские мистики будут рисовать на стенах своих монастырей пентаграммы «золотого сечения», спасаясь от Дьявола. При этом учёные — от Пачоли до Эйнштейна — будут искать, но так и не найдут его точного значения. Безконечный ряд после запятой — 1,6180339887… Странная, загадочная, необъяснимая вещь — эта божественная пропорция мистическим образом сопутствует всему живому. Неживая природа не знает, что такое «золотое сечение». Но вы непременно увидите эту пропорцию и в изгибах морских раковин, и в форме цветов, и в облике жуков, и в красивом человеческом теле. Всё живое и всё красивое — всё подчиняется божественному закону, имя которому — «золотое сечение». Так что же такое «золотое сечение»? Что это за идеальное, божественное сочетание? Может быть это закон красоты? Или всё-таки он — мистическая тайна? Научный феномен или этический принцип? Ответ неизвестен до сих пор. Точнее — нет, известен. «Золотое сечение» — это и то, и другое, и третье. Только не по отдельности, а одновременно… И в этом его подлинная загадка, его великая тайна.
Наверное, трудно найти надёжную меру для объективной оценки самой красоты, и одной логикой тут не обойдешься. Однако здесь поможет опыт тех, для кого поиск красоты был самим смыслом жизни, кто сделал это своей профессией. Это, прежде всего, люди искусства, как мы их называем: художники, архитекторы, скульпторы, музыканты, писатели. Но это и люди точных наук, прежде всего, — математики.
Доверяя глазу больше, чем другим органам чувств, Человек в первую очередь учился различать окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежит сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определённом отношении друг к другу и к целому. Принцип золотого сечения — высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.
ЗОЛОТОЕ СЕЧЕНИЕ — ГАРМОНИЧЕСКАЯ ПРОПОРЦИЯ
В математике пропорцией называют равенство двух отношений:
a:b=c:d.
Отрезок прямой АВ можно разделить на две части следующими способами:
- на две равные части — АВ:АС=АВ:ВС;
- на две неравные части в любом отношении (такие части пропорции не образуют);
- таким образом, когда АВ:АС=АС:ВС.
Последнее и есть золотое деление (сечение).
Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей, другими словами, меньший отрезок так относится к большему, как больший ко всему
a:b=b:c или с:b=b:а.
Геометрическое изображение золотой пропорции
Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.
Деление отрезка прямой по золотому сечению. BC=1/2AB; CD=BC
Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
Отрезки золотой пропорции выражаются безконечной дробью AE=0,618…, если АВ принять за единицу, ВЕ=0,382… Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая 38 частям.
Свойства золотого сечения описываются уравнением:
x2-x-1=0.
Решение этого уравнения:
ВТОРОЕ ЗОЛОТОЕ СЕЧЕНИЕ
Болгарский журнал «Отечество» опубликовал статью Цветана Цекова-Карандаша «О втором золотом сечении», которое вытекает из основного сечения и даёт другое отношение 44: 56.
Такая пропорция обнаружена в архитектуре.
Построение второго золотого сечения
Деление осуществляется следующим образом. Отрезок АВ делится в пропорции золотого сечения. Из точки С восставляется перпендикуляр СD. Радиусом АВ находится точка D, которая соединяется линией с точкой А. Прямой угол АСD делится пополам. Из точки С проводится линия до пересечения с линией AD. Точка Е делит отрезок AD в отношении 56:44.
Деление прямоугольника линией второго золотого сечения
На рисунке показано положение линии второго золотого сечения. Она находится посередине между линией золотого сечения и средней линией прямоугольника.
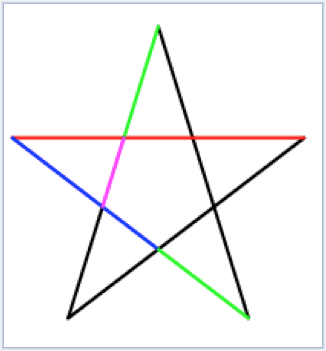
ЗОЛОТОЙ ТРЕУГОЛЬНИК (пентаграмма)
Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой.
Построение правильного пятиугольника и пентаграммы
Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер. Пусть O — центр окружности, A — точка на окружности и Е — середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE=ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 360 при вершине, а основание, отложенное на боковую сторону, делит её в пропорции золотого сечения.
Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1 откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника.
Построение золотого треугольника
ИСТОРИЯ ЗОЛОТОГО СЕЧЕНИЯ
Принято считать, что понятие о золотом делении ввёл в научный обиход Пифагор, древнегреческий философ и математик. Есть предположение, что Пифагор своё знание золотого деления позаимствовал у египтян и вавилонян.
И действительно, пропорции пирамиды Хеопса, храмов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашёл, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображённый на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.
Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.
Динамические прямоугольники

ИКОСАЭДР И ДОДЕКАЭДР
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
Античный циркуль золотого сечения
В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» даётся геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвящённым.
В средние века пентаграмма подверглась демонизации (как, впрочем, и многое, что почиталось божественным в античном язычестве) и нашла приют в оккультных науках. Однако Возрождение вновь выносит на свет и пентаграмму, и золотое сечение. Так, широкое хождение в тот период утверждения гуманизма обрела схема, описывающая строение человеческого тела.
К такой картинке, по сути, воспроизводящей пентаграмму, неоднократно прибегал и Леонардо да Винчи. Её интерпретация: тело человека обладает божественным совершенством, ибо заложенные в нём пропорции такие же, как в главной небесной фигуре. Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.
Лука Пачоли прекрасно понимал значение науки для искусства.
В 1496 г. по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «О божественной пропорции» (De divina proportione, 1497, изд. в Венеции в 1509 г.) с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Такая пропорция лишь одна, а единственность — высочайшее свойство Бога. В ней воплощено святое триединство. Эта пропорция не может быть выражена доступным числом, остаётся скрытой и тайной и самими математиками называется иррациональной (так и Бог не может быть ни определен, ни разъяснён словами). Бог никогда не изменяется и представляет всё во всем и всё в каждой своей части, так и золотое сечение для всякой непрерывной и определённой величины (независимо от того, большая она или малая) одно и то же, не может быть ни изменено, ни по-иному воспринято рассудком. Бог вызвал к бытию небесную добродетель, иначе называемую пятой субстанцией, с её помощью и четыре других простых тела (четыре стихии — землю, воду, воздух, огонь), а на их основе вызвал к бытию всякую другую вещь в природе; так и наша священная пропорция, согласно Платону в «Тимее», даёт формальное бытие самому небу, ибо ему приписывается вид тела, называемого додекаэдром, который невозможно построить без золотого сечения. Таковы аргументы Пачоли.

В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет: «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать».
Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведённой через кончики средних пальцев опущенных рук, нижняя часть лица — ртом и т.д. Известен пропорциональный циркуль Дюрера.
Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).
Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, — писал он, — что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».
Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).
Если на прямой произвольной длины, отложить отрезок m, рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов.
Построение шкалы отрезков золотой пропорции
В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребёнка». Вновь «открыто» золотое сечение было в середине XIX в.
В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив её универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».
Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа — важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13:8=1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8:5=1,6. У новорожденного пропорция составляет отношение 1:1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела — длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону. Следующая его книга имела название «Золотое деление как основной морфологический закон в природе и искусстве». В 1876 г. в России была издана небольшая книжка, почти брошюра, с изложением этого труда Цейзинга. Автор укрылся под инициалами Ю.Ф.В. В этом издании не упомянуто ни одно произведение живописи.
В конце XIX — начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т.д.
ЗОЛОТОЕ СЕЧЕНИЕ И СИММЕТРИЯ
Золотое сечение нельзя рассматривать само по себе, отдельно, без связи с симметрией. Великий русский кристаллограф Г.В. Вульф (1863-1925) считал золотое сечение одним из проявлений симметрии.

РЯД ФИБОНАЧЧИ
С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи. Он много путешествовал по Востоку, познакомил Европу с арабскими цифрами. В 1202 г. вышел в свет его математический труд «Книга об абаке» (счётной доске), в котором были собраны все известные на то время задачи.

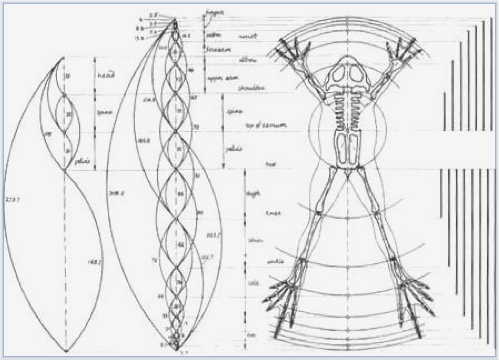
Взгляните на этот скелет лягушки и посмотрите, как каждая косточка соответствует модели пропорции Ф точно так, как и в теле человека.
ОБОБЩЁННОЕ ЗОЛОТОЕ СЕЧЕНИЕ
Учёные продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта. Возникают методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создаётся даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.
Одним из достижений в этой области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений.
Ряд Фибоначчи (1, 1, 2, 3, 5, 
Действительно, зададимся числовым параметром S, который может принимать любые значения: 0, 1, 2, 3, 4, 5… Рассмотрим числовой ряд, S+1, первых членов которого — единицы, а каждый из последующих равен сумме двух членов предыдущего и отстоящего от предыдущего на S шагов. Если n-й член этого ряда мы обозначим через ?S(n), то получим общую формулу ?S(n)=?S(n-1)+?S(n-S-1).
Очевидно, что при S=0 из этой формулы мы получим «двоичный» ряд, при S=1 — ряд Фибоначчи, при S=2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.
В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения xS+1-xS-1=0.
Нетрудно показать, что при S=0 получается деление отрезка пополам, а при S=1 — знакомое классическое золотое сечение.
Отношения соседних S-чисел Фибоначчи с абсолютной математической точностью совпадают в пределе с золотыми S-пропорциями! Математики в таких случаях говорят, что золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.
Факты, подтверждающие существование золотых S-сечений в природе, приводит белорусский ученый Э.М. Сороко в книге «Структурная гармония систем» (Минск, «Наука и техника», 1984). Оказывается, например, что хорошо изученные двойные сплавы обладают особыми, ярко выраженными функциональными свойствами (устойчивы в термическом отношении, тверды, износостойки, устойчивы к окислению и т.п.) только в том случае, если удельные веса исходных компонентов связаны друг с другом одной из золотых S-пропорций. Это позволило автору выдвинуть гипотезу о том, что золотые S-сечения есть числовые инварианты самоорганизующихся систем. Будучи подтверждённой, экспериментально, эта гипотеза может иметь фундаментальное значение для развития синергетики — новой области науки, изучающей процессы в самоорганизующихся системах.
С помощью кодов золотой S-пропорции можно выразить любое действительное число в виде суммы степеней золотых S-пропорций с целыми коэффициентами.
Принципиальное отличие такого способа кодирования чисел заключается в том, что основания новых кодов, представляющие собой золотые S-пропорции, при S>0 оказываются иррациональными числами. Таким образом, новые системы счисления с иррациональными основаниями как бы ставят «с головы на ноги» исторически сложившуюся иерархию отношений между числами рациональными и иррациональными. Дело в том, что сначала были «открыты» числа натуральные; затем их отношения — числа рациональные. И лишь позже, после открытия пифагорейцами несоизмеримых отрезков, на свет появились иррациональные числа. Скажем, в десятичной, пятеричной, двоичной и других классических позиционных системах счисления в качестве своеобразной первоосновы были выбраны натуральные числа: 10, 5, 2, из которых уже по определённым правилам конструировались все другие натуральные, а также рациональные и иррациональные числа.
Своего рода альтернативой существующим способам счисления выступает новая, иррациональная, система, в качестве первоосновы начала счисления которой выбрано иррациональное число (являющееся, напомним, корнем уравнения золотого сечения); через него уже выражаются другие действительные числа.
В такой системе счисления любое натуральное число всегда представимо в виде конечной — а не бесконечной, как думали ранее! — суммы степеней любой из золотых S-пропорций. Это одна из причин, почему «иррациональная» арифметика, обладая удивительной математической простотой и изяществом, как бы вобрала в себя лучшие качества классической двоичной и «Фибоначчиевой» арифметик.
ПРИНЦИПЫ ФОРМООБРАЗОВАНИЯ В ПРИРОДЕ
Всё, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах: рост вверх или расстилание по поверхности земли и закручивание по спирали.
Раковина закручена по спирали. Если её развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Спирали очень распространены в природе. Представление о золотом сечении будет неполным, если не сказать о спирали.
Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал её и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение её шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике.
Еще Гёте подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно.
Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке (филотаксис), семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетёт паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. Гёте называл спираль «кривой жизни».
Ряд Мандельброта
Золотая спираль тесно связана с циклами. Современная наука о хаосе изучает простые циклические операции с обратной связью и порождённые ими фрактальные формы, неизвестные ранее. Рисунок показывает известный ряд Мандельброта — страницу из словаря безконечности индивидуальных паттернов, называемых юлианскими рядами. Некоторые учёные связывают ряд Мандельброта с генетическим кодом клеточных ядер. Последовательное увеличение сечений раскрывает изумительные по своей художественной сложности фракталы. И тут тоже присутствуют логарифмические спирали! Это тем более важно, что и ряд Мандельброта, и юлианские ряды не являются изобретением человеческого разума. Они возникают из области первообразов Платона. Как сказал врач Р. Пенроуз, «они подобны горе Эверест»
Среди придорожных трав растёт ничем не примечательное растение — цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок.
Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок ещё меньшего размера и снова выброс.
Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий — 38, четвертый — 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определённые пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.
Цикорий
У многих бабочек соотношение размеров грудной и брюшной частей тела отвечает золотой пропорции. Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2, 3, 5, 8. Стрекоза также создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.
В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции — длина её хвоста так относится к длине остального тела, как 62 к 38.
Ящерица живородящая
И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы — симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.
Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.
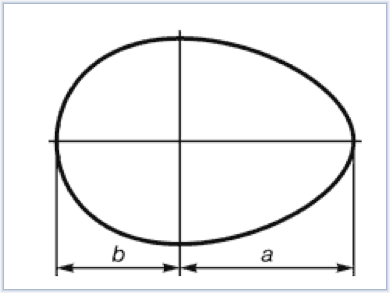
Большой интерес представляет исследование форм птичьих яиц. Их всевозможные формы колеблются между двумя крайними типами: один из них может быть вписан в прямоугольник золотого сечения, другой в прямоугольник с модулем 1,272 (корень золотой пропорции)
Бивни слонов и вымерших мамонтов, когти львов, и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль.
В живой природе широко распространены формы, основанные на «пентагональной» симметрии (морские звезды, морские ежи, цветы).
Золотое сечение присутствует в строении всех кристаллов, но большинство кристаллов микроскопически малы, так что мы не можем разглядеть их невооруженным глазом. Однако снежинки, также представляющие собой водные кристаллы, вполне доступны нашему взору. Все изысканной красоты фигуры, которые образуют снежинки, все оси, окружности и геометрические фигуры в снежинках также всегда, без исключений, построены по совершенной чёткой формуле золотого сечения.
В микромире трёхмерные логарифмические формы, построенные по золотым пропорциям, распространены повсеместно. К примеру, многие вирусы имеют трёхмерную геометрическую форму икосаэдра. Пожалуй, самый известный из таких вирусов — вирус Адено. Белковая оболочка вируса Адено формируется из 252 единиц белковых клеток, расположенных в определенной последовательности. В каждом углу икосаэдра расположены по 12 единиц белковых клеток в форме пятиугольной призмы, и из этих углов простираются шипообразные структуры.
Вирус Адено
Впервые золотое сечение в строении вирусов обнаружили в 1950-хх гг. ученые из Лондонского Биркбекского Колледжа А. Клуг и Д. Каспар. Первым логарифмическую форму явил в себе вирус Polyo. Форма этого вируса оказалась аналогичной с формой вируса Rhino.
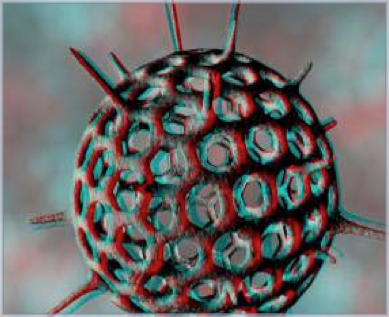
Комментарий Клюга ещё раз напоминает о предельно очевидной истине: в строении даже микроскопического организма, который учёные классифицируют как «самую примитивную форму жизни», в данном случае в вирусе, присутствует чёткий замысел и осуществлён разумный проект. Этот проект несопоставим по своему совершенству и точности исполнения с самыми передовыми архитектурными проектами, созданными людьми. К примеру, проектами, созданными гениальным архитектором Букминстером Фуллером.
Трёхмерные модели додекаэдра и икосаэдра присутствуют также и в строении скелетов одноклеточных морских микроорганизмов радиолярий (лучевиков), скелет которых создан из кремнезёма.
Радиолярии формируют своё тело весьма изысканной, необычной красоты. Форма их составляет правильный додекаэдр, причём из каждого его угла прорастает псевдоудлиннение-конечность и иные необычные формы-наросты.
Великий Гёте, поэт, естествоиспытатель и художник (он рисовал и писал акварелью), мечтал о создании единого учения о форме, образовании и преобразовании органических тел. Это он ввёл в научный обиход термин морфология.
Пьер Кюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды.
Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.
ТЕЛО ЧЕЛОВЕКА И ЗОЛОТОЕ СЕЧЕНИЕ
Все кости человека выдержаны в пропорции золотого сечения. Пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению. Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенными.
Золотые пропорции в частях тела человека
Если принять центром человеческого тела точку пупа, а расстояние между ступнёй человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1.618.
- расстояние от уровня плеча до макушки головы и размера головы равно 1:1.618;
- расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1.618;
- расстояние точки пупа до коленей и от коленей до ступней равно 1:1.618;
- расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1.618;
- собственно точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора;
- расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618;
- расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618;
- высота лица/ширина лица;
- центральная точка соединения губ до основания носа/длина носа;
- высота лица/расстояние от кончика подбородка до центральной точки соединения губ;
- ширина рта/ширина носа;
- ширина носа/расстояние между ноздрями;
- расстояние между зрачками/расстояние между бровями.
Достаточно лишь приблизить сейчас вашу ладонь к себе и внимательно посмотреть на указательный палец, и вы сразу же найдёте в нём формулу золотого сечения.
Каждый палец нашей руки состоит из трёх фаланг. Сумма длинн двух первых фаланг пальца в соотношении со всей длиной пальца и даёт число золотого сечения (за исключением большого пальца).
Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения.
У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, то есть всего 10, но за исключением двух двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 — есть числа последовательности Фибоначчи.
Также следует отметить тот факт, что у большинства людей расстояние между концами расставленных рук равно росту.
Истины золотого сечения внутри нас и в нашем пространстве. Особенность бронхов, составляющих лёгкие человека, заключена в их асимметричности. Бронхи состоят из двух основных дыхательных путей, один из которых (левый) длиннее, а другой (правый) короче. Было установлено, что эта асимметричность продолжается и в ответвлениях бронхов, во всех более мелких дыхательных путях. Причем соотношение длины коротких и длинных бронхов также составляет золотое сечение и равно 1:1,618.
Давление крови изменяется в процессе работы сердца. Наибольшей величины оно достигает в левом желудочке сердца в момент его сжатия (систолы). В артериях во время систолы желудочков сердца кровяное давление достигает максимальной величины, равной 115-125 мм ртутного столбца у молодого, здорового человека. В момент расслабления сердечной мышцы (диастола) давление уменьшается до 70-80 мм рт.ст. Отношение максимального (систолического) к минимальному (диастолическому) давлению равно в среднем 1,6, то есть близко к золотой пропорции.
Если взять за единицу среднее давление крови в аорте, то систолическое давление крови в аорте составляет 0,382, а диастолическое 0,618, то есть их отношение соответствует золотой пропорции. Это означает, что работа сердца в отношении временных циклов и изменения давления крови оптимизированы по одному и тому же принципу закону золотой пропорции.
Молекула ДНК состоит из двух вертикально переплетённых между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем — одна стомиллионная доля сантиметра).
Строение участка спирали молекулы ДНК
Так вот 21 и 34 — это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины, и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотого сечения 1:1,618.
ЗОЛОТОЕ СЕЧЕНИЕ В СКУЛЬПТУРЕ
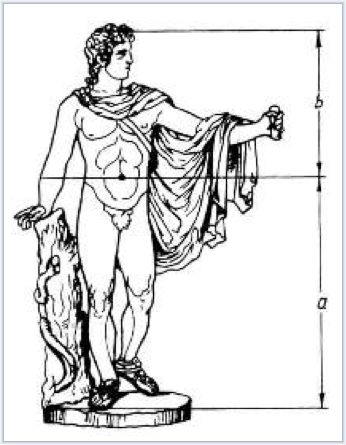
Известна золотая пропорция статуи Аполлона Бельведерского: рост изображенного человека делится пупочной линией в золотом сечении.
ЗОЛОТОЕ СЕЧЕНИЕ В АРХИТЕКТУРЕ
В книгах о «золотом сечении» можно найти замечание о том, что в архитектуре, как и в живописи, всё зависит от положения наблюдателя, и если некоторые пропорции в здании с одной стороны кажутся образующими «золотое сечение», то с других точек зрения они будут выглядеть иначе. «Золотое сечение» даёт наиболее спокойное соотношение размеров тех или иных длин.
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).
На рисунках виден целый ряд закономерностей, связанных с золотым сечением. Пропорции здания можно выразить через различные степени числа Ф=0,618…
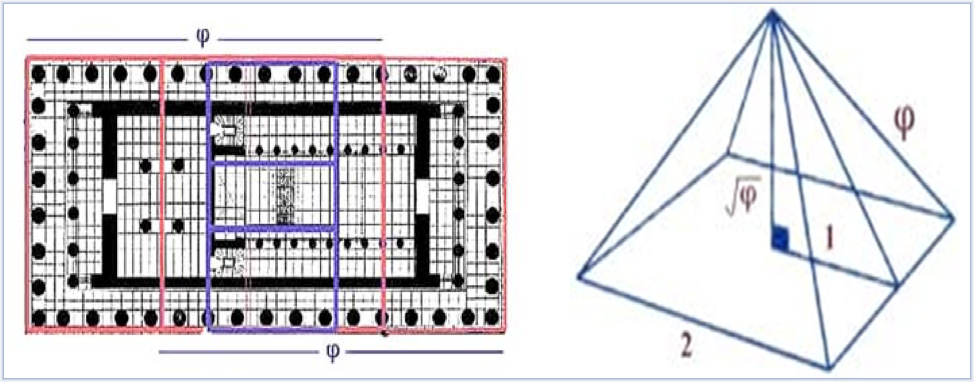
На плане пола Парфенона также можно заметить «золотые прямоугольники».
Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери (Нотр-дам де Пари), и в пирамиде Хеопса.
Не только египетские пиpамиды постpоены в соответствии с совеpшенными пpопоpциями золотого сечения; то же самое явление обнаpужено и у мексиканских пиpамид.

Известный русский архитектор М. Казаков в своем творчестве широко использовал «золотое сечение». Его талант был многогранным, но в большей степени он раскрылся в многочисленных осуществлённых проектах жилых домов и усадеб. Например, «золотое сечение» можно обнаружить в архитектуре здания сената в Кремле. По проекту М. Казакова в Москве была построена Голицынская больница, которая в настоящее время называется Первой клинической больницей имени Н.И. Пирогова.
Петровский дворец в Москве. Построен по проекту М.Ф. Казакова
Еще один архитектурный шедевр Москвы — дом Пашкова — является одним из наиболее совершенных произведений архитектуры В. Баженова.
Дом Пашкова
Прекрасное творение В. Баженова прочно вошло в ансамбль центра современной Москвы, обогатило его. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 г. При восстановлении здание приобрело более массивные формы. Не сохранилась и внутренняя планировка здания, о которой дают представления только чертёж нижнего этажа.
Многие высказывания зодчего заслуживают внимания и в наши дни. О своём любимом искусстве В. Баженов говорил: «Архитектура главнейшие имеет три предмета: красоту, спокойность и прочность здания… К достижению сего служит руководством знание пропорции, перспектива, механика или вообще физика, а всем им общим вождём является рассудок».
ЗОЛОТОЕ СЕЧЕНИЕ В МУЗЫКЕ
Любое музыкальное произведение имеет временное протяжение и делится некоторыми «эстетическими вехами» на отдельные части, которые обращают на себя внимание и облегчают восприятие в целом. Этими вехами могут быть динамические и интонационные кульминационные пункты музыкального произведения. Отдельные временные интервалы музыкального произведения, соединяемые «кульминационным событием», как правило, находятся в соотношении Золотого сечения.
Ещё в 1925 году искусствовед Л.Л. Сабанеев, проанализировав 1770 музыкальных произведений 42 авторов, показал, что подавляющее большинство выдающихся сочинений можно легко разделить на части или по теме, или по интонационному строю, или по ладовому строю, которые находятся между собой в отношении золотого сечения. Причём, чем талантливее композитор, тем в большем количестве его произведений найдено золотых сечений. По мнению Сабанеева, золотое сечение приводит к впечатлению особой стройности музыкального сочинения. Этот результат Сабанеев проверил на всех 27 этюдах Шопена. Он обнаружил в них 178 золотых сечений. При этом оказалось, что не только большие части этюдов делятся по длительности в отношении золотого сечения, но и части этюдов внутри зачастую делятся в таком же отношении.
Композитор и ученый М.А. Марутаев подсчитал количество тактов в знаменитой сонате «Аппассионата» и нашёл ряд интересных числовых соотношений. В частности, в разработке — центральной структурной единице сонаты, где интенсивно развиваются темы и сменяют друг друга тональности, — два основных раздела. В первом — 43,25 такта, во втором — 26,75. Отношение 43,25:26,75=0,618:0,382=1,618 даёт золотое сечение.
Наибольшее количество произведений, в которых имеется Золотое сечение, у Аренского (95%), Бетховена (97%), Гайдна (97%), Моцарта (91%), Шопена (92%), Шуберта (91%).
Если музыка — гармоническое упорядочение звуков, то поэзия — гармоническое упорядочение речи. Чёткий ритм, закономерное чередование ударных и безударных слогов, упорядоченная размерность стихотворений, их эмоциональная насыщенность делают поэзию родной сестрой музыкальных произведений. Золотое сечение в поэзии в первую очередь проявляется как наличие определённого момента стихотворения (кульминации, смыслового перелома, главной мысли произведения) в строке, приходящейся на точку деления общего числа строк стихотворения в золотой пропорции. Так, если стихотворение содержит 100 строк, то первая точка Золотого сечения приходится на 62-ю строку (62%), вторая — на 38-ю (38%) и т.д. Произведения Александра Сергеевича Пушкина, и в том числе «Евгений Онегин», — тончайшее соответствие золотой пропорции! Произведения Шота Руставели и М.Ю. Лермонтова также построены по принципу Золотого сечения.
Страдивари писал, что с помощью золотого сечения он определял места для f-образных вырезов на корпусах своих знаменитых скрипок.
ЗОЛОТОЕ СЕЧЕНИЕ В ПОЭЗИИ

Многое в структуре поэтических произведений роднит этот вид искусства с музыкой. Чёткий ритм, закономерное чередование ударных и безударных слогов, упорядоченная размерность стихотворений, их эмоциональная насыщенность делают поэзию родной сестрой музыкальных произведений. Каждый стих обладает своей музыкальной формой, своей ритмикой и мелодией. Можно ожидать, что в строении стихотворений проявятся некоторые черты музыкальных произведений, закономерности музыкальной гармонии, а следовательно, и золотая пропорция.
Начнём с величины стихотворения, то есть количества строк в нём. Казалось бы, этот параметр стихотворения может изменяться произвольно. Однако оказалось, что это не так. Например, проведенный Н. Васютинским анализ стихотворений А.С. Пушкина показал, что размеры стихов распределены весьма неравномерно; оказалось, что Пушкин явно предпочитает размеры в 5, 8, 13, 21 и 34 строк (числа Фибоначчи).
Многими исследователями было замечено, что стихотворения подобны музыкальным произведениям; в них также существуют кульминационные пункты, которые делят стихотворение в пропорции золотого сечения. Рассмотрим, например, стихотворение А.С. Пушкина «Сапожник»:
И в обуви ошибку указал;
Взяв тотчас кисть, исправился художник,
Вот, подбочась, сапожник продолжал:
«Мне кажется, лицо немного криво…
А эта грудь, не слишком ли нага?
Тут Апеллес прервал нетерпеливо:
«Суди, дружок, не выше сапога!»
Есть у меня приятель на примете:
Не ведаю, в каком бы он предмете
Был знатоком, хоть строг он на словах,
Но черт его несет судить о свете:
Попробуй он судить о сапогах!
Проведём анализ этой притчи. Стихотворение состоит из 13 строк. В нём выделяется две смысловые части: первая в 8 строк и вторая (мораль притчи) в 5 строк (13, 8, 5 — числа Фибоначчи).
Одно из последних стихотворений Пушкина «Не дорого ценю я громкие права…» состоит из 21 строки и в нём выделяется две смысловые части: в 13 и 8 строк:
Не дорого ценю я громкие права,
От коих не одна кружится голова.
Я не ропщу о том, что отказали боги
Мне в сладкой участи оспаривать налоги
Или мешать царям друг с другом воевать;
И мало горя мне, свободно ли печать
Морочит олухов, иль чуткая цензура
В журнальных замыслах стесняет балагура.
Все это, видите ль, слова, слова, слова.
Иные, лучшие, мне дороги права:
Иная, лучшая, потребна мне свобода:
Зависеть от царя, зависеть от народа –
Не все ли нам равно? Бог с ними.
Никому
Отчета не давать, себе лишь самому
Служить и угождать; для власти, для ливреи
Не гнуть ни совести, ни помыслов, ни шеи;
По прихоти своей скитаться здесь и там,
Дивясь божественным природы красотам,
И пред созданьями искусств и вдохновенья
Трепеща радостно в восторгах умиленья,
Вот счастье! Вот права…
Характерно, что и первая часть этого стиха (13 строк) по смысловому содержанию делится на 8 и 5 строк, то есть всё стихотворение построено по законам золотой пропорции.
Представляет несомненный интерес анализ романа «Евгений Онегин», сделанный Н. Васютинским. Этот роман состоит из 8 глав, в каждой из них в среднем около 50 стихов. Наиболее совершенной, наиболее отточенной и эмоционально насыщенной является восьмая глава. В ней 51 стих. Вместе с письмом Евгения к Татьяне (60 строк) это точно соответствует числу Фибоначчи 55!
Н. Васютинский констатирует: «Кульминацией главы является объяснение Евгения в любви к Татьяне — строка «Бледнеть и гаснуть … вот блаженство!» Эта строка делит всю восьмую главу на две части: в первой 477 строк, а во второй — 295 строк. Их отношение равно 1,617! Тончайшее соответствие величине золотой пропорции! Это великое чудо гармонии, совершённое гением Пушкина!».
Э. Розенов провел анализ многих поэтических произведений М.Ю. Лермонтова, Шиллера, А.К. Толстого и также обнаружил в них «золотое сечение».

Главная часть стихотворения состоит из 13 семистиший, то есть из 91 строки. Разделив её золотым сечением (91:1,618=56,238), убеждаемся, что точка деления находится в начале 57-го стиха, где стоит короткая фраза: «Ну, ж был денек!» Именно эта фраза представляет собой «кульминационный пункт возбужденного ожидания», завершающей первую часть стихотворения (ожидание боя) и открывающий вторую его часть (описание боя).
Таким образом, золотое сечение играет в поэзии весьма осмысленную роль, выделяя кульминационный пункт стихотворения.
Многие исследователи поэмы Шота Руставели «Витязь в тигровой шкуре» отмечают исключительную гармоничность и мелодичность его стиха. Эти свойства поэмы грузинский учёный, академик Г.В. Церетели относит за счёт сознательного использования поэтом золотого сечения как в формировании формы поэмы, так и в построении ее стихов.

Установлено, что в поэме Руставели из 1587 строф больше половины (863) построены по принципу золотого сечения.
В наше время родился новый вид искусства — кино, вобравший в себя драматургию действия, живопись, музыку. В выдающихся произведениях киноискусства правомерно искать проявления золотого сечения. Первым это сделал создатель шедевра мирового кино «Броненосец Потёмкин» кинорежиссер Сергей Эйзенштейн. В построении этой картины он сумел воплотить основной принцип гармонии — золотое сечение. Как отмечает сам Эйзенштейн, красный флаг на мачте восставшего броненосца (точка апогея фильма) взвивается в точке золотой пропорции, отсчитываемой от конца фильма.
ЗОЛОТОЕ СЕЧЕНИЕ В ШРИФТАХ И БЫТОВЫХ ПРЕДМЕТАХ
Особый вид изобразительного искусства Древней Греции следует выделить изготовление и роспись всевозможных сосудов. В изящной форме легко угадываются пропорции золотого сечения.
В живописи и скульптуре храмов, на предметах домашнего обихода древние египтяне чаще всего изображали богов и фараонов. Были установлены каноны изображения стоящего человека, идущего, сидящего и т.д. Художники обязаны были заучивать отдельные формы и схемы изображения по таблицам и образцам. Художники Древней Греции совершали специальные путешествия в Египет, чтобы поучиться умению пользоваться каноном.
ОПТИМАЛЬНЫЕ ФИЗИЧЕСКИЕ ПАРАМЕТРЫ ВНЕШНЕЙ СРЕДЫ
Известно, что максимальная громкость звука, которая вызывает болевые ощущения, равна 130 децибеллам. Если разделить этот интервал золотой пропорцией 1,618, то получим 80 децибелл, которые характерны для громкости человеческого крика. Если теперь 80 децибелл разделить золотой пропорцией, то получим 50 децибелл, что соответствует громкости человеческой речи. Наконец, если разделить 50 децибелл квадратом золотой пропорции 2,618, то получим 20 децибелл, что соответствует шёпоту человека. Таким образом, все характерные параметры громкости звука взаимосвязаны через золотую пропорцию.
При температуре 18-200C интервал влажности 40-60% считается оптимальным. Границы оптимального диапазона влажности могут быть получены, если абсолютную влажность 100% дважды разделить золотым сечением:100/2,618 = 38,2% (нижняя граница); 100/1,618=61,8% (верхняя граница).
При давлении воздуха 0,5 МПа у человека возникают неприятные ощущения, ухудшается его физическая и психологическая деятельность. При давлении 0,3-0,35 МПа разрешается только кратковременная работа, а при давлении 0,2 МПа разрешается работать не более 8 мин. Все эти характерные параметры связаны между собой золотой пропорцией:0,5/1,618=0,31 МПа; 0,5/2,618=0,19 МПа.
Граничными параметрами температуры наружного воздуха, в пределах которых возможно нормальное существование (а, главное, стало возможным происхождение) человека является диапазон температур от 0 до +(57-58)0С. Очевидно, по первой границе пояснений можно не приводить.
Разделим указанный диапазон положительных температур золотым сечением. При этом получим две границы (обе границы являются характерными для организма человека температурами): первая соответствует температуре, вторая граница соответствует максимально возможной температуре наружного воздуха для организма человека.
ЗОЛОТОЕ СЕЧЕНИЕ В ЖИВОПИСИ
Данное открытие у художников того времени получило название «золотое сечение» картины.
Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнёт читать мои труды».
Он снискал славу непревзойденного художника, великого учёного, гения, предвосхитившего многие изобретения, которые не были осуществлены вплоть до XX в.
Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится «обо всём на свете».
Он писал справа налево неразборчивым почерком и левой рукой. Это самый известный, из существующих, образец зеркального письма.
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Существует очень много версий об истории этого портрета. Вот одна из них.
Однажды Леонардо да Винчи получил заказ от банкира Франческо деле Джокондо написать портрет молодой женщины, жены банкира, Монны Лизы. Женщина не была красива, но в ней привлекала простота и естественность облика. Леонардо согласился писать портрет. Его модель была печальной и грустной, но Леонардо рассказал ей сказку, услышав которую, она стала живой и интересной.
СКАЗКА. Жил-был один бедный человек, было у него четыре сына: три умных, а один из них и так, и сяк. И вот пришла за отцом смерть. Перед тем, как расстаться с жизнью, он позвал к себе детей и сказал: «Сыны мои, скоро я умру. Как только вы схороните меня, заприте хижину и идите на край света добывать себе счастья. Пусть каждый из вас чему-нибудь научится, чтобы мог кормить сам себя». Отец умер, а сыновья разошлись по свету, договорившись спустя три года вернуться на поляну родной рощи. Пришёл первый брат, который научился плотничать, срубил дерево и обтесал его, сделал из него женщину, отошел немного и ждет. Вернулся второй брат, увидел деревянную женщину и, так как он был портной, в одну минуту одел её: как искусный мастер он сшил для неё красивую шёлковую одежду. Третий сын украсил женщину золотом и драгоценными камнями — ведь он был ювелир. Наконец, пришел четвертый брат. Он не умел плотничать и шить, он умел только слушать, что говорит земля, деревья, травы, звери и птицы, знал ход небесных тел и ещё умел петь чудесные песни. Он запел песню, от которой заплакали притаившиеся за кустами братья. Песней этой он оживил женщину, она улыбнулась и вздохнула. Братья бросились к ней и каждый кричал одно и то же: «Ты должна быть моей женой». Но женщина ответила: «Ты меня создал — будь мне отцом. Ты меня одел, а ты украсил — будьте мне братьями. А ты, что вдохнул в меня душу и научил радоваться жизни, ты один мне нужен на всю жизнь».
Кончив сказку, Леонардо взглянул на Монну Лизу, её лицо озарилось светом, глаза сияли. Потом, точно пробудившись от сна, она вздохнула, провела по лицу рукой и без слов пошла на свое место, сложила руки и приняла обычную позу. Но дело было сделано — художник пробудил равнодушную статую; улыбка блаженства, медленно исчезая с её лица, осталась в уголках рта и трепетала, придавая лицу изумительное, загадочное и чуть лукавое выражение, как у человека, который узнал тайну и, бережно её храня, не может сдержать торжество. Леонардо молча работал, боясь упустить этот момент, этот луч солнца, осветивший его скучную модель…
Трудно отметить, что замечали в этом шедевре искусства, но все говорили о том глубоком знании Леонардо строения человеческого тела, благодаря которому ему удалось уловить эту, как бы загадочную, улыбку. Говорили о выразительности отдельных частей картины и о пейзаже, небывалом спутнике портрета. Толковали о естественности выражения, о простоте позы, о красоте рук. Художник сделал ещё небывалое: на картине изображен воздух, он окутывает фигуру прозрачной дымкой. Несмотря на успех, Леонардо был мрачен, положение во Флоренции показалось художнику тягостным, он собрался в дорогу. Не помогли ему напоминания о нахлынувших заказах.
Золотое сечение в картине И.И. Шишкина «Сосновая роща». На этой знаменитой картине И.И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны — освещённый солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен — при желании можно с успехом продолжить деление картины по золотому сечению и дальше.
Сосновая роща
Наличие в картине ярких вертикалей и горизонталей, делящих её в отношении золотого сечения, придает ей характер уравновешенности и спокойствия в соответствии с замыслом художника. Когда же замысел художника иной, если, скажем, он создает картину с бурно развивающимся действием, подобная геометрическая схема композиции (с преобладанием вертикалей и горизонталей) становится неприемлемой.
В.И. Суриков. «Боярыня Морозова»
Роли её отведена средняя часть картины. Она окована точкой высшего взлёта и точкой низшего спадания сюжета картины: взлёт руки Морозовой с двуперстным крестным знамением, как высшая точка; беспомощно протянутая к той же боярыне рука, но на этот раз рука старухи — нищей странницы, рука, из-под которой вместе с последней надеждой на спасение выскальзывает конец розвальней.
А как обстоит дело с «высшей точкой»? На первый взгляд имеем кажущееся противоречие: ведь сечение А1В1, отстоящее на 0,618… от правого края картины, проходит не через руку, не даже через голову или глаз боярыни, а оказывается где-то перед ртом боярыни.
Золотое сечение режет здесь действительно по самому главному. В нём, и именно в нём — величайшая сила Морозовой.
Нет живописи более поэтичной, чем живопись Боттичелли Сандро, и нет у великого Сандро картины более знаменитой, чем его «Венера». Для Боттичелли его Венера — воплощение идеи универсальной гармонии «золотого сечения», господствующего в природе. Пропорциональный анализ Венеры убеждает нас в этом.
Венера

Хитроумная комбинация двух треугольников также построена в соответствии с пропорцией золотого сечения: она может быть вписана в прямоугольник с соотношением сторон 5/8. Этот чертеж удивительно легко вставляется в верхний участок архитектуры. Верхний угол треугольника упирается в замковый камень арки на ближнем к зрителю участке, нижний — в точку схода перспектив, а боковой участок обозначает пропорции пространственного разрыва между двумя частями арок.
Золотая спираль в картине Рафаэля «Избиение младенцев». В отличие от золотого сечения, ощущение динамики, волнения проявляется, пожалуй, сильней всего в другой простой геометрической фигуре — спирали. Многофигурная композиция, выполненная в 1509 — 1510 годах Рафаэлем, когда прославленный живописец создавал свои фрески в Ватикане, как раз отличается динамизмом и драматизмом сюжета. Рафаэль так и не довёл свой замысел до завершения, однако его эскиз был гравирован неизвестным итальянским графиком Маркантинио Раймонди, который на основе этого эскиза и создал гравюру «Избиение младенцев».
Избиение младенцев
Если на подготовительном эскизе Рафаэля мысленно провести линии, идущие от смыслового центра композиции — точки, где пальцы воина сомкнулись вокруг лодыжки ребенка, вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесённым мечом и затем вдоль фигур такой же группы в правой части эскиза (на рисунке эти линии проведены красным цветом), а после этого соединить эти куски кривой пунктиром, то с очень большой точностью получается золотая спираль. Это можно проверить, измеряя отношение длин отрезков, высекаемых спиралью на прямых, проходящих через начало кривой.
ЗОЛОТОЕ СЕЧЕНИЕ И ВОСПРИЯТИЕ ИЗОБРАЖЕНИЯ
О способности зрительного анализатора человека выделять объекты, построенные по алгоритму золотого сечения, как красивые, привлекательные и гармоничные, известно давно. Золотое сечение даёт ощущение наиболее совершенного единого целого. Формат многих книг соответствует золотому сечению. Оно выбирается для окон, живописных полотен и конвертов, марок, визиток. Человек может ничего не знать о числе Ф, но в строении предметов, а также в последовательности событий он подсознательно находит элементы золотой пропорции.
При выборе прямоугольников в обычном состоянии в 1/2 случаев предпочтение отдается квадрату. Правое полушарие предпочитает золотое сечение и отвергает вытянутый прямоугольник. Наоборот, левое полушарие тяготеет к удлиненным пропорциям и отвергает золотое сечение.
При копировании этих прямоугольников наблюдалось следующее: когда активно правое полушарие — пропорции в копиях выдерживались наиболее точно; при активности левого полушария — пропорции всех прямоугольников искажались, прямоугольники вытягивались (квадрат срисовывался как прямоугольник с отношением сторон 1:1,2; пропорции вытянутого прямоугольника резко увеличивались и достигали 1:2,8). Наиболее сильно искажались пропорции «золотого» прямоугольника; его пропорции в копиях становились пропорциями прямоугольника 1:2,08.
При рисовании собственных рисунков преобладают пропорции, близкие к золотому сечению, и вытянутые. В среднем пропорции составляют 1:2, при этом правое полушарие отдает предпочтение пропорциям золотого сечения, левое полушарие отходит от пропорций золотого сечения и вытягивает рисунок.
А теперь нарисуйте несколько прямоугольников, измерьте их стороны и найдите соотношение сторон. Какое полушарие у Вас преобладает?
ЗОЛОТОЕ СЕЧЕНИЕ В ФОТОГРАФИИ
Примером использования золотого сечения в фотографии является расположение ключевых компонентов кадра в точках, которые расположены в 3/8 и 5/8 от краёв кадра. Можно это проиллюстрировать следующим примером: фотография кота, который расположен в произвольном месте кадра.
Теперь условно поделим кадр на отрезки, в пропорции по 1.62 общей длины от каждой стороны кадра. В местах пересечения отрезков и будут основные «зрительные центры», в которых стоит разместить необходимые ключевые элементы изображения. Перенесём нашего кота в точки «зрительных центров».
ЗОЛОТОЕ СЕЧЕНИЕ И КОСМОС

Однако один случай, который, казалось бы, противоречил закону: между Марсом и Юпитером не было планеты. Cосредоточенное наблюдение за этим участком неба привело к открытию пояса астероидов. Произошло это после смерти Тициуса в начале XIX в. Pяд Фибоначчи используют широко: с его помощью представляют архитектонику и живых существ, и рукотворных сооружений, и строение Галактик. Эти факты — свидетельства независимости числового ряда от условий его проявления, что является одним из признаков его универсальности.
Две Золотых Спирали галактики совместимы со Звездой Давида.
Обратите внимание на звёзды, выходящие из галактики по белой спирали. Точно на 1800 от одной из спиралей выходит другая развёртывающаяся спираль… Долгое время астрономы просто считали, что всё, что там есть — это то, что мы видим; если что-то видимо, то оно существует. Они либо совершенно не замечали невидимой части Реальности, либо они не считали её важной. Но невидимая сторона нашей Реальности в действительности значительно больше видимой стороны и, вероятно, важнее… Иными словами, видимая часть Реальности значительно меньше, нежели один процент от целого — почти ничто. На самом деле, наш настоящий дом — невидимая вселенная…
Во Вселенной все известные человечеству галактики и все тела в них существуют в форме спирали, соответствующей формуле золотого сечения. В спирали нашей галактики лежит коэффициент золотого сечения
ЗАКЛЮЧЕНИЕ
Природа, понимаемая как весь мир в многообразии его форм, состоит, как бы, из двух частей: живой и неживой природы. Для творений неживой природы характерна высокая устойчивость, слабая изменчивость, если судить в масштабах человеческой жизни. Человек рождается, живёт, стареет, умирает, а гранитные горы остаются такими же и планеты вращаются вокруг Солнца также, как и во времена Пифагора.
Мир живой природы предстает перед нами совсем иным — подвижным, изменчивым и удивительно разнообразным. Жизнь демонстрирует нам фантастический карнавал разнообразия и неповторимости творческих комбинаций! Мир неживой природы — это прежде всего мир симметрии, придающий его творениям устойчивость и красоту. Мир природы — это прежде всего мир гармонии, в которой действует «закон золотого сечения».
В современном мире наука приобретает особое значение, в связи с усилением воздействия человека на природу. Важными задачами на современном этапе являются поиск новых путей сосуществования человека и природы, изучение философских, социальных, экономических, образовательных и других проблем, стоящих перед обществом.
В данной работе было рассмотрено влияние свойств «золотого сечения» на живую и не живую природу, на исторический ход развития истории человечества и планеты в целом. Анализируя всё вышеизложенное можно ещё раз подивиться грандиозности процесса познания мира, открытием всё новых его закономерностей и сделать вывод: принцип золотого сечения — высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе. Можно ожидать, что законы развития различных систем природы, законы роста не очень разнообразны и прослеживаются в самых различных образованьях. В этом и проявляется единство природы. Идея такого единства, основанная на проявлении одних и тех же закономерностей в разнородных явлениях природы, сохранила свою актуальность от Пифагора до наших дней.
Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.
Золотое сечение – гармоническая пропорция
В математике пропорцией (лат. proportio) называют равенство двух отношений: a : b = c : d.
Отрезок прямой АВ можно разделить на две части следующими способами:
-
на две равные части – АВ : АС = АВ : ВС;
-
на две неравные части в любом отношении (такие части пропорции не образуют);
-
таким образом, когда АВ : АС = АС : ВС.
Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему
a : b = b : c или с : b = b : а.
Рис. 1. Геометрическое изображение золотой пропорции
Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.
Рис. 2. Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC
Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618…, если АВ принять за единицу, ВЕ = 0,382… Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.
Свойства золотого сечения описываются уравнением:
x2 – x – 1 = 0.
Решение этого уравнения:
Свойства золотого сечения создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.
Второе золотое сечение
Болгарский журнал «Отечество» (№10, 1983 г.) опубликовал статью Цветана Цекова-Карандаша «О втором золотом сечении», которое вытекает из основного сечения и дает другое отношение 44 : 56.
Такая пропорция обнаружена в архитектуре, а также имеет место при построении композиций изображений удлиненного горизонтального формата.
Рис. 3. Построение второго золотого сечения
Деление осуществляется следующим образом (см. рис.3). Отрезок АВ делится в пропорции золотого сечения. Из точки С восставляется перпендикуляр СD. Радиусом АВ находится точка D, которая соединяется линией с точкой А. Прямой угол АСD делится пополам. Из точки С проводится линия до пересечения с линией AD. Точка Е делит отрезок AD в отношении 56 : 44.
Рис. 4. Деление прямоугольника линией второго золотого сечения
На рис. 4 показано положение линии второго золотого сечения. Она находится посередине между линией золотого сечения и средней линией прямоугольника.
Золотой треугольник
Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой.
Рис. 5. Построение правильного пятиугольника и пентаграммы
Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471…1528). Пусть O – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точкеО, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Рис. 6. Построение золотого треугольника
Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника.
История золотого сечения
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.
Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.
Рис. 7. Динамические прямоугольники
Платон (427…347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
Рис. 8. Античный циркуль золотого сечения
В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.
Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок – бога отца, а весь отрезок – бога духа святого).
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению названиезолотое сечение. Так оно и держится до сих пор как самое популярное.
В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет. «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать».
Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом и т.д. Известен пропорциональный циркуль Дюрера.
Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).
Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».
Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).
Если на прямой произвольной длины, отложить отрезок m, рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов
Рис. 9. Построение шкалы отрезков золотой пропорции
В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь «открыто» золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».
Рис. 10. Золотые пропорции в частях тела человека
Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Рис. 11. Золотые пропорции в фигуре человека
Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону. Следующая его книга имела название «Золотое деление как основной морфологический закон в природе и искусстве». В 1876 г. в России была издана небольшая книжка, почти брошюра, с изложением этого труда Цейзинга. Автор укрылся под инициалами Ю.Ф.В. В этом издании не упомянуто ни одно произведение живописи.
В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т.д.
Ряд Фибоначчи
С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:
| Месяцы | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | и т.д. |
| Пары кроликов | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | и т.д. |
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.
Фибоначчи так же занимался решением практических нужд торговли: с помощью какого наименьшего количества гирь можно взвесить товар? Фибоначчи доказывает, что оптимальной является такая система гирь: 1, 2, 4, 8, 16…
Обобщенное золотое сечение
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.
Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта. Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.
Одним из достижений в этой области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений.
Ряд Фибоначчи (1, 1, 2, 3, 5, 
Действительно, зададимся числовым параметром S, который может принимать любые значения: 0, 1, 2, 3, 4, 5… Рассмотрим числовой ряд, S + 1 первых членов которого – единицы, а каждый из последующих равен сумме двух членов предыдущего и отстоящего от предыдущего на S шагов. Если n-й член этого ряда мы обозначим через φS (n), то получим общую формулу φS (n) = φS (n – 1) + φS (n – S – 1).
Очевидно, что при S = 0 из этой формулы мы получим «двоичный» ряд, при S = 1 – ряд Фибоначчи, при S = 2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.
В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения xS+1 – xS – 1 = 0.
Нетрудно показать, что при S = 0 получается деление отрезка пополам, а при S = 1 –знакомое классическое золотое сечение.
Отношения соседних S-чисел Фибоначчи с абсолютной математической точностью совпадают в пределе с золотыми S-пропорциями! Математики в таких случаях говорят, что золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.
Факты, подтверждающие существование золотых S-сечений в природе, приводит белорусский ученый Э.М. Сороко в книге «Структурная гармония систем» (Минск, «Наука и техника», 1984). Оказывается, например, что хорошо изученные двойные сплавы обладают особыми, ярко выраженными функциональными свойствами (устойчивы в термическом отношении, тверды, износостойки, устойчивы к окислению и т. п) только в том случае, если удельные веса исходных компонентов связаны друг с другом одной из золотых S-пропорций. Это позволило автору выдвинуть гипотезe о том, что золотыеS-сечения есть числовые инварианты самоорганизующихся систем. Будучи подтвержденной экспериментально, эта гипотеза может иметь фундаментальное значение для развития синергетики – новой области науки, изучающей процессы в самоорганизующихся системах.
С помощью кодов золотой S-пропорции можно выразить любое действительное число в виде суммы степеней золотых S-пропорций с целыми коэффициентами.
Принципиальное отличие такого способа кодирования чисел заключается в том, что основания новых кодов, представляющие собой золотые S-пропорции, при S > 0 оказываются иррациональными числами. Таким образом, новые системы счисления с иррациональными основаниями как бы ставят «с головы на ноги» исторически сложившуюся иерархию отношений между числами рациональными и иррациональными. Дело в том, что сначала были «открыты» числа натуральные; затем их отношения – числа рациональные. И лишь позже – после открытия пифагорийцами несоизмеримых отрезков – на свет появились иррациональные числа. Скажем, в десятичной, пятеричной, двоичной и других классических позиционных системах счисления в качестве своеобразной первоосновы были выбраны натуральные числа – 10, 5, 2, – из которых уже по определенным правилам конструировались все другие натуральные, а также рациональные и иррациональные числа.
Своего рода альтернативой существующим способам счисления выступает новая, иррациональная система, в качестве первоосновы, начала счисления которой выбрано иррациональное число (являющееся, напомним, корнем уравнения золотого сечения); через него уже выражаются другие действительные числа.
В такой системе счисления любое натуральное число всегда представимо в виде конечной – а не бесконечной, как думали ранее! – суммы степеней любой из золотых S-пропорций. Это одна из причин, почему «иррациональная» арифметика, обладая удивительной математической простотой и изяществом, как бы вобрала в себя лучшие качества классической двоичной и «Фибоначчиевой» арифметик.
Принципы формообразования в природе
Все, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали.
Раковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Спирали очень распространены в природе. Представление о золотом сечении будет неполным, если не сказать о спирали.
Рис. 12. Спираль Архимеда
Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике.
Еще Гете подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке (филотаксис), семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. Гете называл спираль «кривой жизни».
Среди придорожных трав растет ничем не примечательное растение – цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок.
Рис. 13. Цикорий
Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.
Рис. 14. Ящерица живородящая
В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38.
И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы – симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.
Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.
Рис. 15. Яйцо птицы
Великий Гете, поэт, естествоиспытатель и художник (он рисовал и писал акварелью), мечтал о создании единого учения о форме, образовании и преобразовании органических тел. Это он ввел в научный обиход термин морфология.
Пьер Кюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды.
Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.
Золотое сечение и симметрия
Золотое сечение нельзя рассматривать само по себе, отдельно, без связи с симметрией. Великий русский кристаллограф Г.В. Вульф (1863…1925) считал золотое сечение одним из проявлений симметрии.
Золотое деление не есть проявление асимметрии, чего-то противоположного симметрии Согласно современным представлениям золотое деление – это асимметричная симметрия. В науку о симметрии вошли такие понятия, как статическая и динамическая симметрия. Статическая симметрия характеризует покой, равновесие, а динамическая – движение, рост. Так, в природе статическая симметрия представлена строением кристаллов, а в искусстве характеризует покой, равновесие и неподвижность. Динамическая симметрия выражает активность, характеризует движение, развитие, ритм, она – свидетельство жизни. Статической симметрии свойственны равные отрезки, равные величины. Динамической симметрии свойственно увеличение отрезков или их уменьшение, и оно выражается в величинах золотого сечения возрастающего или убывающего ряда.
ПРОДОЛЖЕНИЕ СТАТЬИ ЧИТАЙТЕ ВОТ ТУТ
Вспомните и посмотрите, что такое Капля «принца Руперта», а так же освежите в памяти Рекорды ХИМИИ
Каждый член последовательности, начиная с третьего, равен сумме двух предыдущих, а отношение соседних чисел ряда приближается к отношению золотого деления.
Последовательность Фибоначчи имеет весьма любопытные особенности, не последняя из которых – почти постоянная взаимосвязь между числами.
· Сумма любых двух соседних чисел равна следующему числу в последовательности. Например 3 + 5 = 8; 5 + 8 = 13 и т.д.
· Отношение любого числа в последовательности к следующему приближается к 0,618. Например 1 : 1 = 1; 1 : 2 = 0,5; 3 : 5 = 0,6; 5 : 8 = 0,625; 8 :
13 = 0,615; 15 : 21 = 0,619.
· Отношение любого числа к предыдущему приблизительно равно 1,618 (величина обратная 0,618). Например 13 : 8 = 1,625; 21 : 13 = 1,615; 34 : 21=
1,619. Чем большие числа последовательности берем, тем больше они приближаются к величине 0,618 и 1,618.
· Отношение любого числа к следующему за ним через одно приближается к 0,382, а к предшествующему через одно – 2,618. Например: 13 : 34 = 0,382,
а 34 : 13 = 2,615.
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и животном мире, не говоря
уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.
В настоящее время числа Фибоначчи усиленно изучаются бизнесменами и экономистами. После ряда весьма успешных предсказаний и операций на рынке ценных бумаг инженер Ральф
Hельсон Эллиотт опубликовал в 1939 году серию статей в журнале Financial World Magazine. В них впервые была представлена его точка зрения, что движения индекса Доу-Джонса подчиняются определенным
ритмам и они могут быть сведены к суммационной последовательности Фибоначчи. Если вы разберетесь с числами Фибоначчи и волнами Эллиота, то можете разбогатеть, играя на бирже ценных бумаг. В книге
«Закон природы – секрет Вселенной», вышедшей в 1946 году, Эллиот утверждает, что его теория охватывает не только поведение фондовых индексов, но и более общие законы природы, управляющие
деятельностью человеческого общества.
В начале 20 века американец Марк Барр предложил обозначать число 1,618… греческой буквой Ф (Фи).

Line segments in the golden ratio |
|
| Representations | |
|---|---|
| Decimal | 1.618033988749894…[1] |
| Algebraic form |  |
| Continued fraction |  |
| Binary | 1.10011110001101110111… |
| Hexadecimal | 1.9E3779B97F4A7C15… |
A golden rectangle with long side a and short side b (shaded red, right) and a square with sides of length a (shaded blue, left) combine to form a similar golden rectangle with long side a + b and short side a. This illustrates the relationship
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities 


where the Greek letter phi (




The golden ratio was called the extreme and mean ratio by Euclid,[2] and the divine proportion by Luca Pacioli,[3] and also goes by several other names.[b]
Mathematicians have studied the golden ratio’s properties since antiquity. It is the ratio of a regular pentagon’s diagonal to its side and thus appears in the construction of the dodecahedron and icosahedron.[7] A golden rectangle—that is, a rectangle with an aspect ratio of 
Some 20th-century artists and architects, including Le Corbusier and Salvador Dalí, have proportioned their works to approximate the golden ratio, believing it to be aesthetically pleasing. These uses often appear in the form of a golden rectangle.
Calculation
Two quantities 


One method for finding 

Therefore,
Multiplying by 
which can be rearranged to
The quadratic formula yields two solutions:

Because 


History
According to Mario Livio,
Some of the greatest mathematical minds of all ages, from Pythagoras and Euclid in ancient Greece, through the medieval Italian mathematician Leonardo of Pisa and the Renaissance astronomer Johannes Kepler, to present-day scientific figures such as Oxford physicist Roger Penrose, have spent endless hours over this simple ratio and its properties. … Biologists, artists, musicians, historians, architects, psychologists, and even mystics have pondered and debated the basis of its ubiquity and appeal. In fact, it is probably fair to say that the Golden Ratio has inspired thinkers of all disciplines like no other number in the history of mathematics.[11]
— The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number
Ancient Greek mathematicians first studied the golden ratio because of its frequent appearance in geometry;[12] the division of a line into «extreme and mean ratio» (the golden section) is important in the geometry of regular pentagrams and pentagons.[13] According to one story, 5th-century BC mathematician Hippasus discovered that the golden ratio was neither a whole number nor a fraction (an irrational number), surprising Pythagoreans.[14] Euclid’s Elements (c. 300 BC) provides several propositions and their proofs employing the golden ratio,[15][c] and contains its first known definition which proceeds as follows:[16]
A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.[17][d]
The golden ratio was studied peripherally over the next millennium. Abu Kamil (c. 850–930) employed it in his geometric calculations of pentagons and decagons; his writings influenced that of Fibonacci (Leonardo of Pisa) (c. 1170–1250), who used the ratio in related geometry problems but did not observe that it was connected to the Fibonacci numbers.[19]
Luca Pacioli named his book Divina proportione (1509) after the ratio; the book, largely plagiarized from Piero della Francesca, explored its properties including its appearance in some of the Platonic solids.[20][21] Leonardo da Vinci, who illustrated Pacioli’s book, called the ratio the sectio aurea (‘golden section’).[22] Though it is often said that Pacioli advocated the golden ratio’s application to yield pleasing, harmonious proportions, Livio points out that the interpretation has been traced to an error in 1799, and that Pacioli actually advocated the Vitruvian system of rational proportions.[23] Pacioli also saw Catholic religious significance in the ratio, which led to his work’s title. 16th-century mathematicians such as Rafael Bombelli solved geometric problems using the ratio.[24]
German mathematician Simon Jacob (d. 1564) noted that consecutive Fibonacci numbers converge to the golden ratio;[25] this was rediscovered by Johannes Kepler in 1608.[26] The first known decimal approximation of the (inverse) golden ratio was stated as «about 
Geometry has two great treasures: one is the theorem of Pythagoras, the other the division of a line into extreme and mean ratio. The first we may compare to a mass of gold, the second we may call a precious jewel.[28]
18th-century mathematicians Abraham de Moivre, Nicolaus I Bernoulli, and Leonhard Euler used a golden ratio-based formula which finds the value of a Fibonacci number based on its placement in the sequence; in 1843, this was rediscovered by Jacques Philippe Marie Binet, for whom it was named «Binet’s formula».[29] Martin Ohm first used the German term goldener Schnitt (‘golden section’) to describe the ratio in 1835.[30] James Sully used the equivalent English term in 1875.[31]
By 1910, inventor Mark Barr began using the Greek letter Phi (

The zome construction system, developed by Steve Baer in the late 1960s, is based on the symmetry system of the icosahedron/dodecahedron, and uses the golden ratio ubiquitously. Between 1973 and 1974, Roger Penrose developed Penrose tiling, a pattern related to the golden ratio both in the ratio of areas of its two rhombic tiles and in their relative frequency within the pattern.[36] This gained in interest after Dan Shechtman’s Nobel-winning 1982 discovery of quasicrystals with icosahedral symmetry, which were soon afterward explained through analogies to the Penrose tiling.[37]
Mathematics
Irrationality
The golden ratio is an irrational number. Below are two short proofs of irrationality:
Contradiction from an expression in lowest terms
If φ were rational, then it would be the ratio of sides of a rectangle with integer sides (the rectangle comprising the entire diagram). But it would also be a ratio of integer sides of the smaller rectangle (the rightmost portion of the diagram) obtained by deleting a square. The sequence of decreasing integer side lengths formed by deleting squares cannot be continued indefinitely because the positive integers have a lower bound, so φ cannot be rational.
Recall that:
the whole is the longer part plus the shorter part;
the whole is to the longer part as the longer part is to the shorter part.
If we call the whole 




To say that the golden ratio 










By irrationality of √5
Another short proof – perhaps more commonly known – of the irrationality of the golden ratio makes use of the closure of rational numbers under addition and multiplication. If 

Minimal polynomial
The golden ratio φ and its negative reciprocal −φ−1 are the two roots of the quadratic polynomial x2 − x − 1. The golden ratio’s negative −φ and reciprocal φ−1 are the two roots of the quadratic polynomial x2 + x − 1.
The golden ratio is also an algebraic number and even an algebraic integer. It has minimal polynomial
This quadratic polynomial has two roots, 

The golden ratio is also closely related to the polynomial
which has roots 

Golden ratio conjugate and powers
The conjugate root to the minimal polynomial 
The absolute value of this quantity (

This illustrates the unique property of the golden ratio among positive numbers, that
or its inverse:
The conjugate and the defining quadratic polynomial relationship lead to decimal values that have their fractional part in common with 
The sequence of powers of 




any power of 
As a result, one can easily decompose any power of 


If 
Continued fraction and square root
Approximations to the reciprocal golden ratio by finite continued fractions, or ratios of Fibonacci numbers
The formula 
It is in fact the simplest form of a continued fraction, alongside its reciprocal form:
The convergents of these continued fractions (














This means that the constant 
A continued square root form for 

Relationship to Fibonacci and Lucas numbers
Fibonacci numbers and Lucas numbers have an intricate relationship with the golden ratio. In the Fibonacci sequence, each number is equal to the sum of the preceding two, starting with the base sequence 













The sequence of Lucas numbers (not to be confused with the generalized Lucas sequences, of which this is part) is like the Fibonacci sequence, in-which each term is the sum of the previous two, however instead starts with 













Exceptionally, the golden ratio is equal to the limit of the ratios of successive terms in the Fibonacci sequence and sequence of Lucas numbers:[41]
In other words, if a Fibonacci and Lucas number is divided by its immediate predecessor in the sequence, the quotient approximates 
For example, 

These approximations are alternately lower and higher than 

Closed-form expressions for the Fibonacci and Lucas sequences that involve the golden ratio are:
Combining both formulas above, one obtains a formula for 
Between Fibonacci and Lucas numbers one can deduce 
Indeed, much stronger statements are true:
,
.
These values describe 

Successive powers of the golden ratio obey the Fibonacci recurrence, i.e. 
The reduction to a linear expression can be accomplished in one step by using:
This identity allows any polynomial in 
Consecutive Fibonacci numbers can also be used to obtain a similar formula for the golden ratio, here by infinite summation:
In particular, the powers of 


and so forth.[42] The Lucas numbers also directly generate powers of the golden ratio; for 
Rooted in their interconnecting relationship with the golden ratio is the notion that the sum of third consecutive Fibonacci numbers equals a Lucas number, that is 

Both the Fibonacci sequence and the sequence of Lucas numbers can be used to generate approximate forms of the golden spiral (which is a special form of a logarithmic spiral) using quarter-circles with radii from these sequences, differing only slightly from the true golden logarithmic spiral. Fibonacci spiral is generally the term used for spirals that approximate golden spirals using Fibonacci number-sequenced squares and quarter-circles.
Geometry
The golden ratio features prominently in geometry. For example, it is intrinsically involved in the internal symmetry of the pentagon, and extends to form part of the coordinates of the vertices of a regular dodecahedron, as well as those of a 5-cell. It features in the Kepler triangle and Penrose tilings too, as well as in various other polytopes.
Construction
Dividing a line segment by interior division (top) and exterior division (bottom) according to the golden ratio.
Dividing by interior division
- Having a line segment
construct a perpendicular
at point
with
half the length of
Draw the hypotenuse
- Draw an arc with center
and radius
This arc intersects the hypotenuse
at point
- Draw an arc with center
and radius
This arc intersects the original line segment
at point
Point
divides the original line segment
into line segments
and
with lengths in the golden ratio.
Dividing by exterior division
- Draw a line segment
and construct off the point
a segment
perpendicular to
and with the same length as
- Do bisect the line segment
with
- A circular arc around
with radius
intersects in point
the straight line through points
and
(also known as the extension of
). The ratio of
to the constructed segment
is the golden ratio.
Application examples you can see in the articles Pentagon with a given side length, Decagon with given circumcircle and Decagon with a given side length.
Both of the above displayed different algorithms produce geometric constructions that determine two aligned line segments where the ratio of the longer one to the shorter one is the golden ratio.
Golden angle
When two angles that make a full circle have measures in the golden ratio, the smaller is called the golden angle, with measure 
This angle occurs in patterns of plant growth as the optimal spacing of leaf shoots around plant stems so that successive leaves do not block sunlight from the leaves below them.[43]
Golden spiral
Logarithmic spirals are self-similar spirals where distances covered per turn are in geometric progression. Importantly, isosceles golden triangles can be encased by a golden logarithmic spiral, such that successive turns of a spiral generate new golden triangles inside. This special case of logarithmic spirals is called the golden spiral, and it exhibits continuous growth in golden ratio. That is, for every 


As with any logarithmic spiral, for 

Its polar slope 


It has a complementary angle, 
Golden spirals can be symmetrically placed inside pentagons and pentagrams as well, such that fractal copies of the underlying geometry are reproduced at all scales.
In triangles, quadrilaterals, and pentagons
Odom’s construction
Odom’s construction: AB : BC = AC : AB = φ : 1
George Odom found a construction for 
Kepler triangle
Geometric progression of areas of squares on the sides of a Kepler triangle
An isosceles triangle formed from two Kepler triangles maximizes the ratio of its inradius to side length
The Kepler triangle, named after Johannes Kepler, is the unique right triangle with sides in geometric progression:

These side lengths are the three Pythagorean means of the two numbers 

Among isosceles triangles, the ratio of inradius to side length is maximized for the triangle formed by two reflected copies of the Kepler triangle, sharing the longer of their two legs.[45] The same isosceles triangle maximizes the ratio of the radius of a semicircle on its base to its perimeter.[46]
For a Kepler triangle with smallest side length 
Golden triangle and golden gnomon
A golden triangle subdivided by an angle bisector into a smaller golden triangle and a golden gnomon
The golden triangle or sublime triangle is a acute isosceles triangle with apex angle 36° and base angles 72°.[47] Its two equal sides are in the golden ratio to its base. Another isosceles triangle, obtuse, with apex angle 108° and base angle 36°, is called the golden gnomon. The golden ratio is both the ratio of side length to base in the golden triangle, and the ratio of base to side length in the golden gnomon.[48]
Bisecting one of the base angles of the golden triangle subdivides it into a smaller golden triangle and a golden gnomon. Analogously, any acute isosceles triangle can be subdivided into a similar triangle and an obtuse isosceles triangle, but the golden triangle is the only one for which this subdivision is made by the angle bisector, because it is the only isosceles triangle whose base angle is twice its apex angle. The angle bisector of the golden triangle subdivides the side that it meets in the golden ratio, and the areas of the two subdivided pieces are also in the golden ratio.[48]
If the apex angle of the golden gnomon is trisected, the trisector again subdivides it into a smaller golden gnomon and a golden triangle. The trisector subdivides the base in the golden ratio, and the two pieces have areas in the golden ratio. Analogously, any obtuse triangle can be subdivided into a similar triangle and an acute isosceles triangle, but the golden gnomon is the only one for which this subdivision is made by the angle trisector, because it is the only isosceles triangle whose apex angle is three times its base angle.[48]
Golden rectangle
To construct a golden rectangle with only a straightedge and compass in four simple steps:
| Draw a square. |
| Draw a line from the midpoint of one side of the square to an opposite corner. |
| Use that line as the radius to draw an arc that defines the height of the rectangle. |
| Complete the golden rectangle. |
The golden ratio proportions the adjacent side lengths of a golden rectangle in 

Golden rhombus
A golden rhombus is a rhombus whose diagonals are in proportion to the golden ratio, most commonly 
The lengths of its short and long diagonals 


Its area, in terms of 

Its inradius, in terms of side 
Golden rhombi feature in the rhombic triacontahedron (see section below). They also are found in the golden rhombohedron, the Bilinski dodecahedron,[52] and the rhombic hexecontahedron.[51]
Pentagon and pentagram
A pentagram colored to distinguish its line segments of different lengths. The four lengths are in golden ratio to one another.
In a regular pentagon the ratio of a diagonal to a side is the golden ratio, while intersecting diagonals section each other in the golden ratio. The golden ratio properties of a regular pentagon can be confirmed by applying Ptolemy’s theorem to the quadrilateral formed by removing one of its vertices. If the quadrilateral’s long edge and diagonals are 


The diagonal segments of a pentagon form a pentagram, or five-pointed star polygon, whose geometry is quintessentially described by 

Pentagonal and pentagrammic geometry permits us to calculate the following values for 
The triangles formed by two sides and a diagonal of a regular pentagon are golden gnomons; the pentagon can be subdivided in this way into two golden gnomons and a central golden triangle. The five points of a regular pentagram are golden triangles,[48] as are the ten triangles formed by connecting the vertices of a regular decagon to its center point.[53]
Penrose tilings
The kite and dart tiles of the Penrose tiling. The colored arcs divide each edge in the golden ratio; when two tiles share an edge, their arcs must match.
The golden ratio appears prominently in the Penrose tiling, a family of aperiodic tilings of the plane developed by Roger Penrose, inspired by Johannes Kepler’s remark that pentagrams, decagons, and other shapes could fill gaps that pentagonal shapes alone leave when tiled together.[54] Several variations of this tiling have been studied, all of whose prototiles exhibit the golden ratio:
- Penrose’s original version of this tiling used four shapes: regular pentagons and pentagrams, «boat» figures with three points of a pentagram, and «diamond» shaped rhombi.[55]
- The kite and dart Penrose tiling uses kites with three interior angles of 72° and one interior angle of 144°, and darts, concave quadrilaterals with two interior angles of 36°, one of 72°, and one non-convex angle of 216°. Special matching rules restrict how the tiles can meet at any edge, resulting in seven combinations of tiles at any vertex. Both the kites and darts have sides of two lengths, in the golden ratio to each other. The areas of these two tile shapes are also in the golden ratio to each other.[54]
- The kite and dart can each be cut on their symmetry axes into a pair of golden triangles and golden gnomons, respectively. With suitable matching rules, these triangles, called in this context Robinson triangles, can be used as the prototiles for a form of the Penrose tiling.[54][56]
- The rhombic Penrose tiling contains two types of rhombus, a thin rhombus with angles of 36° and 144°, and a thick rhombus with angles of 72° and 108°. All side lengths are equal, but the ratio of the length of sides to the short diagonal in the thin rhombus equals
, as does the ratio of the sides of to the long diagonal of the thick rhombus. As with the kite and dart tiling, the areas of the two rhombi are in the golden ratio to each other. Again, these rhombi can be decomposed into pairs of Robinson triangles.[54]
Original four-tile Penrose tiling
Rhombic Penrose tiling
In the dodecahedron and icosahedron
| Cartesian coordinates of the dodecahedron : | |
| (±1, ±1, ±1) | |
| (0, ±φ, ±1/φ) | |
| (±1/φ, 0, ±φ) | |
| (±φ, ±1/φ, 0) | |
| A nested cube inside the dodecahedron is represented with dotted lines. |
The regular dodecahedron and its dual polyhedron the icosahedron are Platonic solids whose dimensions are related to the golden ratio. An icosahedron is made of 


For a dodecahedron of side 






While for an icosahedron of side 



The volume and surface area of the dodecahedron can be expressed in terms of 


As well as for the icosahedron:

These geometric values can be calculated from their Cartesian coordinates, which also can be given using formulas involving 


Sets of three golden rectangles intersect perpendicularly inside dodecahedra and icosahedra, forming Borromean rings.[58][50] In dodecahedra, pairs of opposing vertices in golden rectangles meet the centers of pentagonal faces, and in icosahedra, they meet at its vertices. In all, the three golden rectangles contain 

A cube can be inscribed in a regular dodecahedron, with some of the diagonals of the pentagonal faces of the dodecahedron serving as the cube’s edges; therefore, the edge lengths are in the golden ratio. The cube’s volume is 



Other polyhedra are related to the dodecahedron and icosahedron or their symmetries, and therefore have corresponding relations to the golden ratio. These include the compound of five cubes, compound of five octahedra, compound of five tetrahedra, the compound of ten tetrahedra, rhombic triacontahedron, icosidodecahedron, truncated icosahedron, truncated dodecahedron, and rhombicosidodecahedron, rhombic enneacontahedron, and Kepler-Poinsot polyhedra, and rhombic hexecontahedron. In four dimensions, the dodecahedron and icosahedron appear as faces of the 120-cell and 600-cell, which again have dimensions related to the golden ratio.
Other properties
The golden ratio’s decimal expansion can be calculated via root-finding methods, such as Newton’s method or Halley’s method, on the equation 














The golden ratio and its conjugate 

Further, they are interchanged by the three maps 













In the complex plane, the fifth roots of unity 



![{textstyle mathbb {Z} [varphi ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c19ab3d8278828be7f591bad1dc4482e4aaac6d)
This also holds for the remaining tenth roots of unity satisfying 
For the gamma function 



When the golden ratio is used as the base of a numeral system (see golden ratio base, sometimes dubbed phinary or 
![{displaystyle mathbb {Z} [varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14f984c2710477c64fca0f16a71928134bdb8201)


The golden ratio also appears in hyperbolic geometry, as the maximum distance from a point on one side of an ideal triangle to the closer of the other two sides: this distance, the side length of the equilateral triangle formed by the points of tangency of a circle inscribed within the ideal triangle, is 
The golden ratio appears in the theory of modular functions as well. For 
Then
and
where 






and

Applications and observations
Architecture
The Swiss architect Le Corbusier, famous for his contributions to the modern international style, centered his design philosophy on systems of harmony and proportion. Le Corbusier’s faith in the mathematical order of the universe was closely bound to the golden ratio and the Fibonacci series, which he described as «rhythms apparent to the eye and clear in their relations with one another. And these rhythms are at the very root of human activities. They resound in man by an organic inevitability, the same fine inevitability which causes the tracing out of the Golden Section by children, old men, savages and the learned.»[66][67]
Le Corbusier explicitly used the golden ratio in his Modulor system for the scale of architectural proportion. He saw this system as a continuation of the long tradition of Vitruvius, Leonardo da Vinci’s «Vitruvian Man», the work of Leon Battista Alberti, and others who used the proportions of the human body to improve the appearance and function of architecture.
In addition to the golden ratio, Le Corbusier based the system on human measurements, Fibonacci numbers, and the double unit. He took suggestion of the golden ratio in human proportions to an extreme: he sectioned his model human body’s height at the navel with the two sections in golden ratio, then subdivided those sections in golden ratio at the knees and throat; he used these golden ratio proportions in the Modulor system. Le Corbusier’s 1927 Villa Stein in Garches exemplified the Modulor system’s application. The villa’s rectangular ground plan, elevation, and inner structure closely approximate golden rectangles.[68]
Another Swiss architect, Mario Botta, bases many of his designs on geometric figures. Several private houses he designed in Switzerland are composed of squares and circles, cubes and cylinders. In a house he designed in Origlio, the golden ratio is the proportion between the central section and the side sections of the house.[69]
Art
Leonardo da Vinci’s illustrations of polyhedra in Pacioli’s Divina proportione have led some to speculate that he incorporated the golden ratio in his paintings. But the suggestion that his Mona Lisa, for example, employs golden ratio proportions, is not supported by Leonardo’s own writings.[70] Similarly, although Leonardo’s Vitruvian Man is often shown in connection with the golden ratio, the proportions of the figure do not actually match it, and the text only mentions whole number ratios.[71][72]
Salvador Dalí, influenced by the works of Matila Ghyka,[73] explicitly used the golden ratio in his masterpiece, The Sacrament of the Last Supper. The dimensions of the canvas are a golden rectangle. A huge dodecahedron, in perspective so that edges appear in golden ratio to one another, is suspended above and behind Jesus and dominates the composition.[70][74]
A statistical study on 565 works of art of different great painters, performed in 1999, found that these artists had not used the golden ratio in the size of their canvases. The study concluded that the average ratio of the two sides of the paintings studied is 







Depiction of the proportions in a medieval manuscript. According to Jan Tschichold: «Page proportion 2:3. Margin proportions 1:1:2:3. Text area proportioned in the Golden Section.»[77]
Books and design
According to Jan Tschichold,
There was a time when deviations from the truly beautiful page proportions

and the Golden Section were rare. Many books produced between 1550 and 1770 show these proportions exactly, to within half a millimeter.[78]
According to some sources, the golden ratio is used in everyday design, for example in the proportions of playing cards, postcards, posters, light switch plates, and widescreen televisions.[79]
Flags
The aspect ratio (width to height ratio) of the flag of Togo was intended to be the golden ratio, according to its designer.[80]
Music
Ernő Lendvai analyzes Béla Bartók’s works as being based on two opposing systems, that of the golden ratio and the acoustic scale,[81] though other music scholars reject that analysis.[82] French composer Erik Satie used the golden ratio in several of his pieces, including Sonneries de la Rose+Croix. The golden ratio is also apparent in the organization of the sections in the music of Debussy’s Reflets dans l’eau (Reflections in Water), from Images (1st series, 1905), in which «the sequence of keys is marked out by the intervals 34, 21, 13 and 8, and the main climax sits at the phi position».[83]
The musicologist Roy Howat has observed that the formal boundaries of Debussy’s La Mer correspond exactly to the golden section.[84] Trezise finds the intrinsic evidence «remarkable», but cautions that no written or reported evidence suggests that Debussy consciously sought such proportions.[85]
Music theorists including Hans Zender and Heinz Bohlen have experimented with the 833 cents scale, a musical scale based on using the golden ratio as its fundamental musical interval. When measured in cents, a logarithmic scale for musical intervals, the golden ratio is approximately 833.09 cents.[86]
Nature
Johannes Kepler wrote that «the image of man and woman stems from the divine proportion. In my opinion, the propagation of plants and the progenitive acts of animals are in the same ratio».[87]
The psychologist Adolf Zeising noted that the golden ratio appeared in phyllotaxis and argued from these patterns in nature that the golden ratio was a universal law.[88] Zeising wrote in 1854 of a universal orthogenetic law of «striving for beauty and completeness in the realms of both nature and art».[89]
However, some have argued that many apparent manifestations of the golden ratio in nature, especially in regard to animal dimensions, are fictitious.[90]
Physics
The quasi-one-dimensional Ising ferromagnet CoNb2O6 (cobalt niobate) has 8 predicted excitation states (with E8 symmetry), that when probed with neutron scattering, showed its lowest two were in golden ratio. Specifically, these quantum phase transitions during spin excitation, which occur at near absolute zero temperature, showed pairs of kinks in its ordered-phase to spin-flips in its paramagnetic phase; revealing, just below its critical field, a spin dynamics with sharp modes at low energies approaching the golden mean.[91]
Optimization
There is no known general algorithm to arrange a given number of nodes evenly on a sphere, for any of several definitions of even distribution (see, for example, Thomson problem or Tammes problem). However, a useful approximation results from dividing the sphere into parallel bands of equal surface area and placing one node in each band at longitudes spaced by a golden section of the circle, i.e. 
The golden ratio is a critical element to golden-section search as well.
Disputed observations
Examples of disputed observations of the golden ratio include the following:
Nautilus shells are often erroneously claimed to be golden-proportioned.
- Specific proportions in the bodies of vertebrates (including humans) are often claimed to be in the golden ratio; for example the ratio of successive phalangeal and metacarpal bones (finger bones) has been said to approximate the golden ratio. There is a large variation in the real measures of these elements in specific individuals, however, and the proportion in question is often significantly different from the golden ratio.[93][94]
- The shells of mollusks such as the nautilus are often claimed to be in the golden ratio.[95] The growth of nautilus shells follows a logarithmic spiral, and it is sometimes erroneously claimed that any logarithmic spiral is related to the golden ratio,[96] or sometimes claimed that each new chamber is golden-proportioned relative to the previous one.[97] However, measurements of nautilus shells do not support this claim.[98]
- Historian John Man states that both the pages and text area of the Gutenberg Bible were «based on the golden section shape». However, according to his own measurements, the ratio of height to width of the pages is
[99]
- Studies by psychologists, starting with Gustav Fechner c. 1876,[100] have been devised to test the idea that the golden ratio plays a role in human perception of beauty. While Fechner found a preference for rectangle ratios centered on the golden ratio, later attempts to carefully test such a hypothesis have been, at best, inconclusive.[101][70]
- In investing, some practitioners of technical analysis use the golden ratio to indicate support of a price level, or resistance to price increases, of a stock or commodity; after significant price changes up or down, new support and resistance levels are supposedly found at or near prices related to the starting price via the golden ratio.[102] The use of the golden ratio in investing is also related to more complicated patterns described by Fibonacci numbers (e.g. Elliott wave principle and Fibonacci retracement). However, other market analysts have published analyses suggesting that these percentages and patterns are not supported by the data.[103]
Egyptian pyramids
The Great Pyramid of Giza (also known as the Pyramid of Cheops or Khufu) has been analyzed by pyramidologists as having a doubled Kepler triangle as its cross-section. If this theory were true, the golden ratio would describe the ratio of distances from the midpoint of one of the sides of the pyramid to its apex, and from the same midpoint to the center of the pyramid’s base. However, imprecision in measurement caused in part by the removal of the outer surface of the pyramid makes it impossible to distinguish this theory from other numerical theories of the proportions of the pyramid, based on pi or on whole-number ratios. The consensus of modern scholars is that this pyramid’s proportions are not based on the golden ratio, because such a basis would be inconsistent both with what is known about Egyptian mathematics from the time of construction of the pyramid, and with Egyptian theories of architecture and proportion used in their other works.[104]
The Parthenon
Many of the proportions of the Parthenon are alleged to exhibit the golden ratio, but this has largely been discredited.[105]
The Parthenon’s façade (c. 432 BC) as well as elements of its façade and elsewhere are said by some to be circumscribed by golden rectangles.[106] Other scholars deny that the Greeks had any aesthetic association with golden ratio. For example, Keith Devlin says, «Certainly, the oft repeated assertion that the Parthenon in Athens is based on the golden ratio is not supported by actual measurements. In fact, the entire story about the Greeks and golden ratio seems to be without foundation.»[107] Midhat J. Gazalé affirms that «It was not until Euclid … that the golden ratio’s mathematical properties were studied.»[108]
From measurements of 15 temples, 18 monumental tombs, 8 sarcophagi, and 58 grave stelae from the fifth century BC to the second century AD, one researcher concluded that the golden ratio was totally absent from Greek architecture of the classical fifth century BC, and almost absent during the following six centuries.[109]
Later sources like Vitruvius (first century BC) exclusively discuss proportions that can be expressed in whole numbers, i.e. commensurate as opposed to irrational proportions.
Modern art
The Section d’Or (‘Golden Section’) was a collective of painters, sculptors, poets and critics associated with Cubism and Orphism.[110] Active from 1911 to around 1914, they adopted the name both to highlight that Cubism represented the continuation of a grand tradition, rather than being an isolated movement, and in homage to the mathematical harmony associated with Georges Seurat.[111] (Several authors have claimed that Seurat employed the golden ratio in his paintings, but Seurat’s writings and paintings suggest that he employed simple whole-number ratios and any approximation of the golden ratio was coincidental.)[112] The Cubists observed in its harmonies, geometric structuring of motion and form, «the primacy of idea over nature», «an absolute scientific clarity of conception».[113] However, despite this general interest in mathematical harmony, whether the paintings featured in the celebrated 1912 Salon de la Section d’Or exhibition used the golden ratio in any compositions is more difficult to determine. Livio, for example, claims that they did not,[114] and Marcel Duchamp said as much in an interview.[115] On the other hand, an analysis suggests that Juan Gris made use of the golden ratio in composing works that were likely, but not definitively, shown at the exhibition.[115][116] Art historian Daniel Robbins has argued that in addition to referencing the mathematical term, the exhibition’s name also refers to the earlier Bandeaux d’Or group, with which Albert Gleizes and other former members of the Abbaye de Créteil had been involved.[117]
Piet Mondrian has been said to have used the golden section extensively in his geometrical paintings,[118] though other experts (including critic Yve-Alain Bois) have discredited these claims.[70][119]
See also
- List of works designed with the golden ratio
- Metallic mean
- Plastic number
- Sacred geometry
- Supergolden ratio
References
Explanatory footnotes
- ^ If the constraint on
and
each being greater than zero is lifted, then there are actually two solutions, one positive and one negative, to this equation.
is defined as the positive solution. The negative solution is
The sum of the two solutions is
, and the product of the two solutions is
.
- ^ Other names include the golden mean, golden section,[4] golden cut,[5] golden proportion, golden number,[6] medial section, and divine section.
- ^ Euclid, Elements, Book II, Proposition 11; Book IV, Propositions 10–11; Book VI, Proposition 30; Book XIII, Propositions 1–6, 8–11, 16–18.
- ^ «῎Ακρον καὶ μέσον λόγον εὐθεῖα τετμῆσθαι λέγεται, ὅταν ᾖ ὡς ἡ ὅλη πρὸς τὸ μεῖζον τμῆμα, οὕτως τὸ μεῖζον πρὸς τὸ ἔλαττὸν.»[18]
- ^ After Classical Greek sculptor Phidias (c. 490–430 BC);[33] Barr later wrote that he thought it unlikely that Phidias actually used the golden ratio.[34]
Citations
- ^ a b c Sloane, N. J. A. (ed.). «Sequence A001622 (Decimal expansion of golden ratio phi (or tau) = (1 + sqrt(5))/2)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^
Euclid. «Book 6, Definition 3». Elements. - ^
Pacioli, Luca (1509). De divina proportione. Venice: Luca Paganinem de Paganinus de Brescia (Antonio Capella). - ^ Livio 2002, pp. 3, 81.
- ^
Summerson, John (1963). Heavenly Mansions and Other Essays on Architecture. New York: W.W. Norton. p. 37.And the same applies in architecture, to the rectangles representing these and other ratios (e.g., the ‘golden cut’). The sole value of these ratios is that they are intellectually fruitful and suggest the rhythms of modular design.
- ^ Herz-Fischler 1998.
- ^ Herz-Fischler 1998, pp. 20–25.
- ^
Strogatz, Steven (2012-09-24). «Me, Myself, and Math: Proportion Control». The New York Times. - ^
Schielack, Vincent P. (1987). «The Fibonacci Sequence and the Golden Ratio». The Mathematics Teacher. 80 (5): 357–358. doi:10.5951/MT.80.5.0357. JSTOR 27965402. This source contains an elementary derivation of the golden ratio’s value. - ^
Peters, J. M. H. (1978). «An Approximate Relation between π and the Golden Ratio». The Mathematical Gazette. 62 (421): 197–198. doi:10.2307/3616690. - ^ Livio 2002, p. 6.
- ^ Livio 2002, p. 4: «… line division, which Euclid defined for … purely geometrical purposes …»
- ^ Livio 2002, pp. 7–8.
- ^ Livio 2002, pp. 4–5.
- ^ Livio 2002, p. 78.
- ^
Hemenway, Priya (2005). Divine Proportion: Phi In Art, Nature, and Science. New York: Sterling. pp. 20–21. - ^ Livio 2002, p. 3.
- ^
Euclid (2007). Euclid’s Elements of Geometry. Translated by Fitzpatrick, Richard. p. 156. ISBN 978-0615179841. - ^ Livio 2002, pp. 88–96.
- ^
Mackinnon, Nick (1993). «The Portrait of Fra Luca Pacioli». The Mathematical Gazette. 77 (479): 130–219. doi:10.2307/3619717. - ^ Livio 2002, pp. 131–132.
- ^
Baravalle, H. V. (1948). «The geometry of the pentagon and the golden section». Mathematics Teacher. 41: 22–31. doi:10.5951/MT.41.1.0022. - ^ Livio 2002, pp. 134–135.
- ^ Livio 2002, p. 141.
- ^
Schreiber, Peter (1995). «A Supplement to J. Shallit’s Paper ‘Origins of the Analysis of the Euclidean Algorithm’«. Historia Mathematica. 22 (4): 422–424. doi:10.1006/hmat.1995.1033. - ^ Livio 2002, pp. 151–152.
- ^
O’Connor, John J.; Robertson, Edmund F. (2001). «The Golden Ratio». MacTutor History of Mathematics archive. Retrieved 2007-09-18. - ^
Fink, Karl (1903). A Brief History of Mathematics. Translated by Beman, Wooster Woodruff; Smith, David Eugene (2nd ed.). Chicago: Open Court. p. 223. (Originally published as Geschichte der Elementar-Mathematik.) - ^
Beutelspacher, Albrecht; Petri, Bernhard (1996). «Fibonacci-Zahlen». Der Goldene Schnitt (in German). Vieweg+Teubner Verlag. pp. 87–98. doi:10.1007/978-3-322-85165-9_6. - ^ Herz-Fischler 1998, pp. 167–170.
- ^ Posamentier & Lehmann 2011, p. 8.
- ^ Posamentier & Lehmann 2011, p. 285.
- ^
Cook, Theodore Andrea (1914). The Curves of Life. London: Constable. p. 420. - ^
Barr, Mark (1929). «Parameters of beauty». Architecture (NY). Vol. 60. p. 325. Reprinted: «Parameters of beauty». Think. Vol. 10–11. IBM. 1944. - ^ Livio 2002, p. 5.
- ^
Gardner, Martin (2001). «7. Penrose Tiles». The Colossal Book of Mathematics. Norton. pp. 73–93. - ^
Livio 2002, pp. 203–209
Gratias, Denis; Quiquandon, Marianne (2019). «Discovery of quasicrystals: The early days». Comptes Rendus Physique. 20 (7–8): 803–816. doi:10.1016/j.crhy.2019.05.009.
Jaric, Marko V. (1989). Introduction to the Mathematics of Quasicrystals. Academic Press. p. x.Although at the time of the discovery of quasicrystals the theory of quasiperiodic functions had been known for nearly sixty years, it was the mathematics of aperiodic Penrose tilings, mostly developed by Nicolaas de Bruijn, that provided the major influence on the new field.
Goldman, Alan I.; Anderegg, James W.; Besser, Matthew F.; Chang, Sheng-Liang; Delaney, Drew W.; Jenks, Cynthia J.; Kramer, Matthew J.; Lograsso, Thomas A.; Lynch, David W.; McCallum, R. William; Shield, Jeffrey E.; Sordelet, Daniel J.; Thiel, Patricia A. (1996). «Quasicrystalline materials». American Scientist. 84 (3): 230–241. JSTOR 29775669. - ^
Martin, George E. (1998). Geometric Constructions. Springer. pp. 13–14. doi:10.1007/978-1-4612-0629-3. - ^
Hailperin, Max; Kaiser, Barbara K.; Knight, Karl W. (1999). Concrete Abstractions: An Introduction to Computer Science Using Scheme. Brooks/Cole. p. 63. - ^
Hardy, G. H.; Wright, E. M. (1960) [1938]. «§11.8. The measure of the closest approximations to an arbitrary irrational». An Introduction to the Theory of Numbers (4th ed.). Oxford University Press. pp. 163–164. - ^
Tattersall, James Joseph (1999). Elementary number theory in nine chapters. Cambridge University Press. p. 28. - ^
Parker, Matt (2014). Things to Make and Do in the Fourth Dimension. Farrar, Straus and Giroux. p. 284. - ^ King, S.; Beck, F.; Lüttge, U. (2004). «On the mystery of the golden angle in phyllotaxis». Plant, Cell and Environment. 27 (6): 685–695. doi:10.1111/j.1365-3040.2004.01185.x.
- ^
Odom, George; van de Craats, Jan (1986). «E3007: The golden ratio from an equilateral triangle and its circumcircle». Problems and solutions. The American Mathematical Monthly. 93 (7): 572. doi:10.2307/2323047. JSTOR 2323047. - ^
Busard, Hubert L. L. (1968). «L’algèbre au Moyen Âge : le «Liber mensurationum» d’Abû Bekr». Journal des Savants (in French and Latin). 1968 (2): 65–124. doi:10.3406/jds.1968.1175. See problem 51, reproduced on p. 98 - ^
Bruce, Ian (1994). «Another instance of the golden right triangle» (PDF). Fibonacci Quarterly. 32 (3): 232–233. - ^
Fletcher, Rachel (2006). «The golden section». Nexus Network Journal. 8 (1): 67–89. doi:10.1007/s00004-006-0004-z. - ^ a b c d
Loeb, Arthur (1992). «The Golden Triangle». Concepts & Images: Visual Mathematics. Birkhäuser. pp. 179–192. doi:10.1007/978-1-4612-0343-8_20. - ^ Posamentier & Lehmann 2011, p. 11.
- ^ a b
Burger, Edward B.; Starbird, Michael P. (2005) [2000]. The Heart of Mathematics: An Invitation to Effective Thinking (2nd ed.). Springer. p. 382. - ^ a b
Grünbaum, Branko (1996). «A new rhombic hexecontahedron» (PDF). Geombinatorics. 6 (1): 15–18. - ^
Senechal, Marjorie (2006). «Donald and the golden rhombohedra». In Davis, Chandler; Ellers, Erich W. (eds.). The Coxeter Legacy. American Mathematical Society. pp. 159–177. ISBN 0-8218-3722-2. - ^
Miller, William (1996). «Pentagons and Golden Triangles». Mathematics in School. 25 (4): 2–4. JSTOR 30216571. - ^ a b c d
Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. pp. 537–547. - ^
Penrose, Roger (1978). «Pentaplexity». Eureka. Vol. 39. p. 32. (original PDF) - ^
Frettlöh, D.; Harriss, E.; Gähler, F. «Robinson Triangle». Tilings Encyclopedia.Clason, Robert G (1994). «A family of golden triangle tile patterns». The Mathematical Gazette. 78 (482): 130–148. doi:10.2307/3618569.
- ^ a b Livio (2002, pp. 70–72)
- ^
Gunn, Charles; Sullivan, John M. (2008). «The Borromean Rings: A video about the New IMU logo». In Sarhangi, Reza; Séquin, Carlo H. (eds.). Proceedings of Bridges 2008. Leeuwarden, the Netherlands. Tarquin Publications. pp. 63–70.; Video at «The Borromean Rings: A new logo for the IMU». International Mathematical Union. - ^
Hume, Alfred (1900). «Some propositions on the regular dodecahedron». The American Mathematical Monthly. 7 (12): 293–295. doi:10.2307/2969130. - ^
Coxeter, H.S.M.; du Val, Patrick; Flather, H.T.; Petrie, J.F. (1938). The Fifty-Nine Icosahedra. Vol. 6. University of Toronto Studies. p. 4.Just as a tetrahedron can be inscribed in a cube, so a cube can be inscribed in a dodecahedron. By reciprocation, this leads to an octahedron circumscribed about an icosahedron. In fact, each of the twelve vertices of the icosahedron divides an edge of the octahedron according to the «golden section.
- ^
Muller, J. M. (2006). Elementary functions : algorithms and implementation (2nd ed.). Boston: Birkhäuser. p. 93. ISBN 978-0817643720. - ^
Yee, Alexander J. (2021-03-13). «Records Set by y-cruncher». numberword.org. Two independent computations done by Clifford Spielman. - ^
Horocycles exinscrits : une propriété hyperbolique remarquable, cabri.net, retrieved 2009-07-21. - ^
Berndt, Bruce C.; Chan, Heng Huat; Huang, Sen-Shan; Kang, Soon-Yi; Sohn, Jaebum; Son, Seung Hwan (1999). «The Rogers–Ramanujan Continued Fraction» (PDF). Journal of Computational and Applied Mathematics. 105 (1–2): 9–24. doi:10.1016/S0377-0427(99)00033-3. - ^
Duffin, Richard J. (1978). «Algorithms for localizing roots of a polynomial and the Pisot Vijayaraghavan numbers». Pacific Journal of Mathematics. 74 (1): 47–56. doi:10.2140/pjm.1978.74.47. - ^ Le Corbusier, The Modulor, p. 25, as cited in
Padovan, Richard (1999). Proportion: Science, Philosophy, Architecture. Taylor & Francis. p. 316. doi:10.4324/9780203477465. - ^
Frings, Marcus (2002). «The Golden Section in Architectural Theory». Nexus Network Journal. 4 (1): 9–32. doi:10.1007/s00004-001-0002-0. - ^ Le Corbusier, The Modulor, p. 35, as cited in
Padovan, Richard (1999). Proportion: Science, Philosophy, Architecture. Taylor & Francis. p. 320. doi:10.4324/9780203477465.Both the paintings and the architectural designs make use of the golden section
- ^
Urwin, Simon (2003). Analysing Architecture (2nd ed.). Routledge. pp. 154–155. - ^ a b c d
Livio, Mario (2002). «The golden ratio and aesthetics». Plus Magazine. Retrieved November 26, 2018. - ^
Devlin, Keith (2007). «The Myth That Will Not Go Away». Retrieved September 26, 2013.Part of the process of becoming a mathematics writer is, it appears, learning that you cannot refer to the golden ratio without following the first mention by a phrase that goes something like ‘which the ancient Greeks and others believed to have divine and mystical properties.’ Almost as compulsive is the urge to add a second factoid along the lines of ‘Leonardo Da Vinci believed that the human form displays the golden ratio.’ There is not a shred of evidence to back up either claim, and every reason to assume they are both false. Yet both claims, along with various others in a similar vein, live on.
- ^
Simanek, Donald E. «Fibonacci Flim-Flam». Archived from the original on January 9, 2010. Retrieved April 9, 2013. - ^
Salvador Dalí (2008). The Dali Dimension: Decoding the Mind of a Genius (DVD). Media 3.14-TVC-FGSD-IRL-AVRO. - ^
Hunt, Carla Herndon; Gilkey, Susan Nicodemus (1998). Teaching Mathematics in the Block. pp. 44, 47. ISBN 1-883001-51-X. - ^
Olariu, Agata (1999). «Golden Section and the Art of Painting». arXiv:physics/9908036. - ^
Tosto, Pablo (1969). La composición áurea en las artes plásticas [The golden composition in the plastic arts] (in Spanish). Hachette. pp. 134–144. - ^
Tschichold, Jan (1991). The Form of the Book. Hartley & Marks. p. 43 Fig 4. ISBN 0-88179-116-4.Framework of ideal proportions in a medieval manuscript without multiple columns. Determined by Jan Tschichold 1953. Page proportion 2:3. margin proportions 1:1:2:3, Text area proportioned in the Golden Section. The lower outer corner of the text area is fixed by a diagonal as well.
- ^
Tschichold, Jan (1991). The Form of the Book. Hartley & Marks. pp. 27–28. ISBN 0-88179-116-4. - ^
Jones, Ronald (1971). «The golden section: A most remarkable measure». The Structurist. 11: 44–52.Who would suspect, for example, that the switch plate for single light switches are standardized in terms of a Golden Rectangle?
Johnson, Art (1999). Famous problems and their mathematicians. Teacher Ideas Press. p. 45.
The Golden Ratio is a standard feature of many modern designs, from postcards and credit cards to posters and light-switch plates.
Stakhov, Alexey P.; Olsen, Scott (2009). «§1.4.1 A Golden Rectangle with a Side Ratio of τ«. The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science. World Scientific. p. 20–21.
A credit card has a form of the golden rectangle
Cox, Simon (2004). Cracking the Da Vinci Code. Barnes & Noble. p. 62.
The Golden Ratio also crops up in some very unlikely places: widescreen televisions, postcards, credit cards and photographs all commonly conform to its proportions.
- ^ Posamentier & Lehmann 2011, chapter 4, footnote 12: «The Togo flag was designed by the artist Paul Ahyi (1930–2010), who claims to have attempted to have the flag constructed in the shape of a golden rectangle».
- ^
Lendvai, Ernő (1971). Béla Bartók: An Analysis of His Music. London: Kahn and Averill. - ^ Livio 2002, p. 190.
- ^
Smith, Peter F. (2003). The Dynamics of Delight: Architecture and Aesthetics. Routledge. p. 83. - ^
Howat, Roy (1983). «1. Proportional structure and the Golden Section». Debussy in Proportion: A Musical Analysis. Cambridge University Press. pp. 1–10. - ^
Trezise, Simon (1994). Debussy: La Mer. Cambridge University Press. p. 53. - ^
Mongoven, Casey (2010). «A style of music characterized by Fibonacci and the golden ratio» (PDF). Congressus Numerantium. 201: 127–138.Hasegawa, Robert (2011). «Gegenstrebige Harmonik in the Music of Hans Zender». Perspectives of New Music. Project Muse. 49 (1): 207–234. doi:10.1353/pnm.2011.0000. JSTOR 10.7757/persnewmusi.49.1.0207.
Smethurst, Reilly (2016). «Two Non-Octave Tunings by Heinz Bohlen: A Practical Proposal». In Torrence, Eve; et al. (eds.). Proceedings of Bridges 2016. Jyväskylä, Finland. Tessellations Publishing. pp. 519–522.
- ^ Livio 2002, p. 154.
- ^
Padovan, Richard (1999). Proportion: Science, Philosophy, Architecture. Taylor & Francis. pp. 305–306. doi:10.4324/9780203477465.Padovan, Richard (2002). «Proportion: Science, Philosophy, Architecture». Nexus Network Journal. 4 (1): 113–122. doi:10.1007/s00004-001-0008-7.
- ^
Zeising, Adolf (1854). «Einleitung [preface]». Neue Lehre von den Proportionen des menschlichen Körpers [New doctrine of the proportions of the human body] (in German). Weigel. pp. 1–10. - ^
Pommersheim, James E.; Marks, Tim K.; Flapan, Erica L., eds. (2010). Number Theory: A Lively Introduction with Proofs, Applications, and Stories. Wiley. p. 82. - ^
Coldea, R.; Tennant, D.A.; Wheeler, E.M.; Wawrzynksa, E.; Prabhakaran, D.; Telling, M.; Habicht, K.; Smeibidl, P.; Keifer, K. (2010). «Quantum Criticality in an Ising Chain: Experimental Evidence for Emergent E8 Symmetry». Science. 327 (5962): 177–180. arXiv:1103.3694. doi:10.1126/science.1180085. - ^
«A Disco Ball in Space». NASA. 2001-10-09. Retrieved 2007-04-16. - ^
Pheasant, Stephen (1986). Bodyspace. Taylor & Francis. - ^
van Laack, Walter (2001). A Better History Of Our World: Volume 1 The Universe. Aachen: van Laach. - ^
Dunlap, Richard A. (1997). The Golden Ratio and Fibonacci Numbers. World Scientific. p. 130. - ^
Falbo, Clement (March 2005). «The golden ratio—a contrary viewpoint». The College Mathematics Journal. 36 (2): 123–134. doi:10.1080/07468342.2005.11922119. - ^
Moscovich, Ivan (2004). The Hinged Square & Other Puzzles. New York: Sterling. p. 122. - ^
Peterson, Ivars (1 April 2005). «Sea shell spirals». Science News. Archived from the original on 3 October 2012. Retrieved 10 November 2008. - ^
Man, John (2002). Gutenberg: How One Man Remade the World with Word. Wiley. pp. 166–167.The half-folio page (30.7 × 44.5 cm) was made up of two rectangles—the whole page and its text area—based on the so called ‘golden section’, which specifies a crucial relationship between short and long sides, and produces an irrational number, as pi is, but is a ratio of about 5:8.
- ^
Fechner, Gustav (1876). Vorschule der Ästhetik [Preschool of Aesthetics] (in German). Leipzig: Breitkopf & Härtel. pp. 190–202. - ^ Livio 2002, p. 7.
- ^
Osler, Carol (2000). «Support for Resistance: Technical Analysis and Intraday Exchange Rates» (PDF). Federal Reserve Bank of New York Economic Policy Review. 6 (2): 53–68. Archived (PDF) from the original on 2007-05-12.38.2 percent and 61.8 percent retracements of recent rises or declines are common,
- ^
Batchelor, Roy; Ramyar, Richard (2005). Magic numbers in the Dow (Report). Cass Business School. pp. 13, 31.
Popular press summaries can be found in:
Stevenson, Tom (2006-04-10). «Not since the ‘big is beautiful’ days have giants looked better». The Daily Telegraph.
«Technical failure». The Economist. 2006-09-23. - ^
Herz-Fischler, Roger (2000). The Shape of the Great Pyramid. Wilfrid Laurier University Press. ISBN 0-88920-324-5. The entire book surveys many alternative theories for this pyramid’s shape. See Chapter 11, «Kepler triangle theory», pp. 80–91, for material specific to the Kepler triangle, and p. 166 for the conclusion that the Kepler triangle theory can be eliminated by the principle that «A theory must correspond to a level of mathematics consistent with what was known to the ancient Egyptians.» See note 3, p. 229, for the history of Kepler’s work with this triangle.Rossi, Corinna (2004). Architecture and Mathematics in Ancient Egypt. Cambridge University Press. pp. 67–68.
there is no direct evidence in any ancient Egyptian written mathematical source of any arithmetic calculation or geometrical construction which could be classified as the Golden Section … convergence to
; see also extensive discussion of multiple alternative theories for the shape of the pyramid and other Egyptian architecture, pp. 7–56, and
itself as a number, do not fit with the extant Middle Kingdom mathematical sources
Rossi, Corinna; Tout, Christopher A. (2002). «Were the Fibonacci series and the Golden Section known in ancient Egypt?». Historia Mathematica. 29 (2): 101–113. doi:10.1006/hmat.2001.2334.
Markowsky, George (1992). «Misconceptions about the Golden Ratio» (PDF). The College Mathematics Journal. Mathematical Association of America. 23 (1): 2–19. doi:10.2307/2686193. Retrieved 2012-06-29.
It does not appear that the Egyptians even knew of the existence of
much less incorporated it in their buildings
- ^ Livio 2002, pp. 74–75.
- ^
Van Mersbergen, Audrey M. (1998). «Rhetorical Prototypes in Architecture: Measuring the Acropolis with a Philosophical Polemic». Communication Quarterly. 46 (2): 194–213. doi:10.1080/01463379809370095. - ^
Devlin, Keith J. (2005). The Math Instinct. New York: Thunder’s Mouth Press. p. 108. - ^
Gazalé, Midhat J. (1999). Gnomon: From Pharaohs to Fractals. Princeton. p. 125. - ^
Foutakis, Patrice (2014). «Did the Greeks Build According to the Golden Ratio?». Cambridge Archaeological Journal. 24 (1): 71–86. doi:10.1017/S0959774314000201. - ^
Le Salon de la Section d’Or, October 1912, Mediation Centre Pompidou - ^
Jeunes Peintres ne vous frappez pas !, La Section d’Or: Numéro spécial consacré à l’Exposition de la «Section d’Or», première année, n° 1, 9 octobre 1912, pp. 1–7 Archived 2020-10-30 at the Wayback Machine, Bibliothèque Kandinsky - ^
Herz-Fischler, Roger (1983). «An Examination of Claims Concerning Seurat and the Golden Number» (PDF). Gazette des Beaux-Arts. 101: 109–112. - ^
Herbert, Robert (1968). Neo-Impressionism. Guggenheim Foundation.[page needed] - ^ Livio 2002, p. 169.
- ^ a b
Camfield, William A. (March 1965). «Juan Gris and the golden section». The Art Bulletin. 47 (1): 128–134. doi:10.1080/00043079.1965.10788819. - ^
Green, Christopher (1992). Juan Gris. Yale. pp. 37–38.Cottington, David (2004). Cubism and Its Histories. Manchester University Press. p. 112, 142.
- ^
Allard, Roger (June 1911). «Sur quelques peintres». Les Marches du Sud-Ouest: 57–64.
Reprinted in
Antliff, Mark; Leighten, Patricia, eds. (2008). A Cubism Reader, Documents and Criticism, 1906–1914. The University of Chicago Press. pp. 178–191. - ^
Bouleau, Charles (1963). The Painter’s Secret Geometry: A Study of Composition in Art. Harcourt, Brace & World. pp. 247–248. - ^ Livio 2002, pp. 177–178.
Works cited
- Herz-Fischler, Roger (1998) [1987]. A Mathematical History of the Golden Number. Dover. ISBN 9780486400075. (Originally titled A Mathematical History of Division in Extreme and Mean Ratio.)
- Livio, Mario (2002). The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number. New York: Broadway Books. ISBN 9780767908153.
- Posamentier, Alfred S.; Lehmann, Ingmar (2011). The Glorious Golden Ratio. Prometheus Books. ISBN 9-781-61614-424-1.
Further reading
- Doczi, György (1981). The Power of Limits: Proportional Harmonies in Nature, Art, and Architecture. Boston: Shambhala.
- Hargittai, István, ed. (1992). Fivefold Symmetry. World Scientific. ISBN 9789810206000.
- Huntley, H. E. (1970). The Divine Proportion: A Study in Mathematical Beauty. New York: Dover. ISBN 978-0-486-22254-7.
- Schaaf, William L., ed. (1967). The Golden Measure (PDF). California School Mathematics Study Group Reprint Series. Stanford University. Archived (PDF) from the original on 2015-04-25.
- Scimone, Aldo (1997). La Sezione Aurea. Storia culturale di un leitmotiv della Matematica. Palermo: Sigma Edizioni. ISBN 978-88-7231-025-0.
- Walser, Hans (2001) [Der Goldene Schnitt 1993]. The Golden Section. Peter Hilton trans. Washington, DC: The Mathematical Association of America. ISBN 978-0-88385-534-8.
External links
- «Golden ratio». Encyclopedia of Mathematics. EMS Press. 2001 [1994].
- «Golden Section» by Michael Schreiber, Wolfram Demonstrations Project, 2007.
- Weisstein, Eric W. «Golden Ratio». MathWorld.
- Knott, Ron. «The Golden section ratio: Phi». Information and activities by a mathematics professor.
- The Myth That Will Not Go Away, by Keith Devlin, addressing multiple allegations about the use of the golden ratio in culture.
- Spurious golden spirals collected by Randall Munroe
- YouTube lecture on Zeno’s mice problem and logarithmic spirals

Line segments in the golden ratio |
|
| Representations | |
|---|---|
| Decimal | 1.618033988749894…[1] |
| Algebraic form |  |
| Continued fraction |  |
| Binary | 1.10011110001101110111… |
| Hexadecimal | 1.9E3779B97F4A7C15… |
A golden rectangle with long side a and short side b (shaded red, right) and a square with sides of length a (shaded blue, left) combine to form a similar golden rectangle with long side a + b and short side a. This illustrates the relationship
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities 


where the Greek letter phi (




The golden ratio was called the extreme and mean ratio by Euclid,[2] and the divine proportion by Luca Pacioli,[3] and also goes by several other names.[b]
Mathematicians have studied the golden ratio’s properties since antiquity. It is the ratio of a regular pentagon’s diagonal to its side and thus appears in the construction of the dodecahedron and icosahedron.[7] A golden rectangle—that is, a rectangle with an aspect ratio of 
Some 20th-century artists and architects, including Le Corbusier and Salvador Dalí, have proportioned their works to approximate the golden ratio, believing it to be aesthetically pleasing. These uses often appear in the form of a golden rectangle.
Calculation
Two quantities 


One method for finding 

Therefore,
Multiplying by 
which can be rearranged to
The quadratic formula yields two solutions:

Because 


History
According to Mario Livio,
Some of the greatest mathematical minds of all ages, from Pythagoras and Euclid in ancient Greece, through the medieval Italian mathematician Leonardo of Pisa and the Renaissance astronomer Johannes Kepler, to present-day scientific figures such as Oxford physicist Roger Penrose, have spent endless hours over this simple ratio and its properties. … Biologists, artists, musicians, historians, architects, psychologists, and even mystics have pondered and debated the basis of its ubiquity and appeal. In fact, it is probably fair to say that the Golden Ratio has inspired thinkers of all disciplines like no other number in the history of mathematics.[11]
— The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number
Ancient Greek mathematicians first studied the golden ratio because of its frequent appearance in geometry;[12] the division of a line into «extreme and mean ratio» (the golden section) is important in the geometry of regular pentagrams and pentagons.[13] According to one story, 5th-century BC mathematician Hippasus discovered that the golden ratio was neither a whole number nor a fraction (an irrational number), surprising Pythagoreans.[14] Euclid’s Elements (c. 300 BC) provides several propositions and their proofs employing the golden ratio,[15][c] and contains its first known definition which proceeds as follows:[16]
A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.[17][d]
The golden ratio was studied peripherally over the next millennium. Abu Kamil (c. 850–930) employed it in his geometric calculations of pentagons and decagons; his writings influenced that of Fibonacci (Leonardo of Pisa) (c. 1170–1250), who used the ratio in related geometry problems but did not observe that it was connected to the Fibonacci numbers.[19]
Luca Pacioli named his book Divina proportione (1509) after the ratio; the book, largely plagiarized from Piero della Francesca, explored its properties including its appearance in some of the Platonic solids.[20][21] Leonardo da Vinci, who illustrated Pacioli’s book, called the ratio the sectio aurea (‘golden section’).[22] Though it is often said that Pacioli advocated the golden ratio’s application to yield pleasing, harmonious proportions, Livio points out that the interpretation has been traced to an error in 1799, and that Pacioli actually advocated the Vitruvian system of rational proportions.[23] Pacioli also saw Catholic religious significance in the ratio, which led to his work’s title. 16th-century mathematicians such as Rafael Bombelli solved geometric problems using the ratio.[24]
German mathematician Simon Jacob (d. 1564) noted that consecutive Fibonacci numbers converge to the golden ratio;[25] this was rediscovered by Johannes Kepler in 1608.[26] The first known decimal approximation of the (inverse) golden ratio was stated as «about 
Geometry has two great treasures: one is the theorem of Pythagoras, the other the division of a line into extreme and mean ratio. The first we may compare to a mass of gold, the second we may call a precious jewel.[28]
18th-century mathematicians Abraham de Moivre, Nicolaus I Bernoulli, and Leonhard Euler used a golden ratio-based formula which finds the value of a Fibonacci number based on its placement in the sequence; in 1843, this was rediscovered by Jacques Philippe Marie Binet, for whom it was named «Binet’s formula».[29] Martin Ohm first used the German term goldener Schnitt (‘golden section’) to describe the ratio in 1835.[30] James Sully used the equivalent English term in 1875.[31]
By 1910, inventor Mark Barr began using the Greek letter Phi (

The zome construction system, developed by Steve Baer in the late 1960s, is based on the symmetry system of the icosahedron/dodecahedron, and uses the golden ratio ubiquitously. Between 1973 and 1974, Roger Penrose developed Penrose tiling, a pattern related to the golden ratio both in the ratio of areas of its two rhombic tiles and in their relative frequency within the pattern.[36] This gained in interest after Dan Shechtman’s Nobel-winning 1982 discovery of quasicrystals with icosahedral symmetry, which were soon afterward explained through analogies to the Penrose tiling.[37]
Mathematics
Irrationality
The golden ratio is an irrational number. Below are two short proofs of irrationality:
Contradiction from an expression in lowest terms
If φ were rational, then it would be the ratio of sides of a rectangle with integer sides (the rectangle comprising the entire diagram). But it would also be a ratio of integer sides of the smaller rectangle (the rightmost portion of the diagram) obtained by deleting a square. The sequence of decreasing integer side lengths formed by deleting squares cannot be continued indefinitely because the positive integers have a lower bound, so φ cannot be rational.
Recall that:
the whole is the longer part plus the shorter part;
the whole is to the longer part as the longer part is to the shorter part.
If we call the whole 




To say that the golden ratio 










By irrationality of √5
Another short proof – perhaps more commonly known – of the irrationality of the golden ratio makes use of the closure of rational numbers under addition and multiplication. If 

Minimal polynomial
The golden ratio φ and its negative reciprocal −φ−1 are the two roots of the quadratic polynomial x2 − x − 1. The golden ratio’s negative −φ and reciprocal φ−1 are the two roots of the quadratic polynomial x2 + x − 1.
The golden ratio is also an algebraic number and even an algebraic integer. It has minimal polynomial
This quadratic polynomial has two roots, 

The golden ratio is also closely related to the polynomial
which has roots 

Golden ratio conjugate and powers
The conjugate root to the minimal polynomial 
The absolute value of this quantity (

This illustrates the unique property of the golden ratio among positive numbers, that
or its inverse:
The conjugate and the defining quadratic polynomial relationship lead to decimal values that have their fractional part in common with 
The sequence of powers of 




any power of 
As a result, one can easily decompose any power of 


If 
Continued fraction and square root
Approximations to the reciprocal golden ratio by finite continued fractions, or ratios of Fibonacci numbers
The formula 
It is in fact the simplest form of a continued fraction, alongside its reciprocal form:
The convergents of these continued fractions (














This means that the constant 
A continued square root form for 

Relationship to Fibonacci and Lucas numbers
Fibonacci numbers and Lucas numbers have an intricate relationship with the golden ratio. In the Fibonacci sequence, each number is equal to the sum of the preceding two, starting with the base sequence 













The sequence of Lucas numbers (not to be confused with the generalized Lucas sequences, of which this is part) is like the Fibonacci sequence, in-which each term is the sum of the previous two, however instead starts with 













Exceptionally, the golden ratio is equal to the limit of the ratios of successive terms in the Fibonacci sequence and sequence of Lucas numbers:[41]
In other words, if a Fibonacci and Lucas number is divided by its immediate predecessor in the sequence, the quotient approximates 
For example, 

These approximations are alternately lower and higher than 

Closed-form expressions for the Fibonacci and Lucas sequences that involve the golden ratio are:
Combining both formulas above, one obtains a formula for 
Between Fibonacci and Lucas numbers one can deduce 
Indeed, much stronger statements are true:
,
.
These values describe 

Successive powers of the golden ratio obey the Fibonacci recurrence, i.e. 
The reduction to a linear expression can be accomplished in one step by using:
This identity allows any polynomial in 
Consecutive Fibonacci numbers can also be used to obtain a similar formula for the golden ratio, here by infinite summation:
In particular, the powers of 


and so forth.[42] The Lucas numbers also directly generate powers of the golden ratio; for 
Rooted in their interconnecting relationship with the golden ratio is the notion that the sum of third consecutive Fibonacci numbers equals a Lucas number, that is 

Both the Fibonacci sequence and the sequence of Lucas numbers can be used to generate approximate forms of the golden spiral (which is a special form of a logarithmic spiral) using quarter-circles with radii from these sequences, differing only slightly from the true golden logarithmic spiral. Fibonacci spiral is generally the term used for spirals that approximate golden spirals using Fibonacci number-sequenced squares and quarter-circles.
Geometry
The golden ratio features prominently in geometry. For example, it is intrinsically involved in the internal symmetry of the pentagon, and extends to form part of the coordinates of the vertices of a regular dodecahedron, as well as those of a 5-cell. It features in the Kepler triangle and Penrose tilings too, as well as in various other polytopes.
Construction
Dividing a line segment by interior division (top) and exterior division (bottom) according to the golden ratio.
Dividing by interior division
- Having a line segment
construct a perpendicular
at point
with
half the length of
Draw the hypotenuse
- Draw an arc with center
and radius
This arc intersects the hypotenuse
at point
- Draw an arc with center
and radius
This arc intersects the original line segment
at point
Point
divides the original line segment
into line segments
and
with lengths in the golden ratio.
Dividing by exterior division
- Draw a line segment
and construct off the point
a segment
perpendicular to
and with the same length as
- Do bisect the line segment
with
- A circular arc around
with radius
intersects in point
the straight line through points
and
(also known as the extension of
). The ratio of
to the constructed segment
is the golden ratio.
Application examples you can see in the articles Pentagon with a given side length, Decagon with given circumcircle and Decagon with a given side length.
Both of the above displayed different algorithms produce geometric constructions that determine two aligned line segments where the ratio of the longer one to the shorter one is the golden ratio.
Golden angle
When two angles that make a full circle have measures in the golden ratio, the smaller is called the golden angle, with measure 
This angle occurs in patterns of plant growth as the optimal spacing of leaf shoots around plant stems so that successive leaves do not block sunlight from the leaves below them.[43]
Golden spiral
Logarithmic spirals are self-similar spirals where distances covered per turn are in geometric progression. Importantly, isosceles golden triangles can be encased by a golden logarithmic spiral, such that successive turns of a spiral generate new golden triangles inside. This special case of logarithmic spirals is called the golden spiral, and it exhibits continuous growth in golden ratio. That is, for every 


As with any logarithmic spiral, for 

Its polar slope 


It has a complementary angle, 
Golden spirals can be symmetrically placed inside pentagons and pentagrams as well, such that fractal copies of the underlying geometry are reproduced at all scales.
In triangles, quadrilaterals, and pentagons
Odom’s construction
Odom’s construction: AB : BC = AC : AB = φ : 1
George Odom found a construction for 
Kepler triangle
Geometric progression of areas of squares on the sides of a Kepler triangle
An isosceles triangle formed from two Kepler triangles maximizes the ratio of its inradius to side length
The Kepler triangle, named after Johannes Kepler, is the unique right triangle with sides in geometric progression:

These side lengths are the three Pythagorean means of the two numbers 

Among isosceles triangles, the ratio of inradius to side length is maximized for the triangle formed by two reflected copies of the Kepler triangle, sharing the longer of their two legs.[45] The same isosceles triangle maximizes the ratio of the radius of a semicircle on its base to its perimeter.[46]
For a Kepler triangle with smallest side length 
Golden triangle and golden gnomon
A golden triangle subdivided by an angle bisector into a smaller golden triangle and a golden gnomon
The golden triangle or sublime triangle is a acute isosceles triangle with apex angle 36° and base angles 72°.[47] Its two equal sides are in the golden ratio to its base. Another isosceles triangle, obtuse, with apex angle 108° and base angle 36°, is called the golden gnomon. The golden ratio is both the ratio of side length to base in the golden triangle, and the ratio of base to side length in the golden gnomon.[48]
Bisecting one of the base angles of the golden triangle subdivides it into a smaller golden triangle and a golden gnomon. Analogously, any acute isosceles triangle can be subdivided into a similar triangle and an obtuse isosceles triangle, but the golden triangle is the only one for which this subdivision is made by the angle bisector, because it is the only isosceles triangle whose base angle is twice its apex angle. The angle bisector of the golden triangle subdivides the side that it meets in the golden ratio, and the areas of the two subdivided pieces are also in the golden ratio.[48]
If the apex angle of the golden gnomon is trisected, the trisector again subdivides it into a smaller golden gnomon and a golden triangle. The trisector subdivides the base in the golden ratio, and the two pieces have areas in the golden ratio. Analogously, any obtuse triangle can be subdivided into a similar triangle and an acute isosceles triangle, but the golden gnomon is the only one for which this subdivision is made by the angle trisector, because it is the only isosceles triangle whose apex angle is three times its base angle.[48]
Golden rectangle
To construct a golden rectangle with only a straightedge and compass in four simple steps:
| Draw a square. |
| Draw a line from the midpoint of one side of the square to an opposite corner. |
| Use that line as the radius to draw an arc that defines the height of the rectangle. |
| Complete the golden rectangle. |
The golden ratio proportions the adjacent side lengths of a golden rectangle in 

Golden rhombus
A golden rhombus is a rhombus whose diagonals are in proportion to the golden ratio, most commonly 
The lengths of its short and long diagonals 


Its area, in terms of 

Its inradius, in terms of side 
Golden rhombi feature in the rhombic triacontahedron (see section below). They also are found in the golden rhombohedron, the Bilinski dodecahedron,[52] and the rhombic hexecontahedron.[51]
Pentagon and pentagram
A pentagram colored to distinguish its line segments of different lengths. The four lengths are in golden ratio to one another.
In a regular pentagon the ratio of a diagonal to a side is the golden ratio, while intersecting diagonals section each other in the golden ratio. The golden ratio properties of a regular pentagon can be confirmed by applying Ptolemy’s theorem to the quadrilateral formed by removing one of its vertices. If the quadrilateral’s long edge and diagonals are 


The diagonal segments of a pentagon form a pentagram, or five-pointed star polygon, whose geometry is quintessentially described by 

Pentagonal and pentagrammic geometry permits us to calculate the following values for 
The triangles formed by two sides and a diagonal of a regular pentagon are golden gnomons; the pentagon can be subdivided in this way into two golden gnomons and a central golden triangle. The five points of a regular pentagram are golden triangles,[48] as are the ten triangles formed by connecting the vertices of a regular decagon to its center point.[53]
Penrose tilings
The kite and dart tiles of the Penrose tiling. The colored arcs divide each edge in the golden ratio; when two tiles share an edge, their arcs must match.
The golden ratio appears prominently in the Penrose tiling, a family of aperiodic tilings of the plane developed by Roger Penrose, inspired by Johannes Kepler’s remark that pentagrams, decagons, and other shapes could fill gaps that pentagonal shapes alone leave when tiled together.[54] Several variations of this tiling have been studied, all of whose prototiles exhibit the golden ratio:
- Penrose’s original version of this tiling used four shapes: regular pentagons and pentagrams, «boat» figures with three points of a pentagram, and «diamond» shaped rhombi.[55]
- The kite and dart Penrose tiling uses kites with three interior angles of 72° and one interior angle of 144°, and darts, concave quadrilaterals with two interior angles of 36°, one of 72°, and one non-convex angle of 216°. Special matching rules restrict how the tiles can meet at any edge, resulting in seven combinations of tiles at any vertex. Both the kites and darts have sides of two lengths, in the golden ratio to each other. The areas of these two tile shapes are also in the golden ratio to each other.[54]
- The kite and dart can each be cut on their symmetry axes into a pair of golden triangles and golden gnomons, respectively. With suitable matching rules, these triangles, called in this context Robinson triangles, can be used as the prototiles for a form of the Penrose tiling.[54][56]
- The rhombic Penrose tiling contains two types of rhombus, a thin rhombus with angles of 36° and 144°, and a thick rhombus with angles of 72° and 108°. All side lengths are equal, but the ratio of the length of sides to the short diagonal in the thin rhombus equals
, as does the ratio of the sides of to the long diagonal of the thick rhombus. As with the kite and dart tiling, the areas of the two rhombi are in the golden ratio to each other. Again, these rhombi can be decomposed into pairs of Robinson triangles.[54]
Original four-tile Penrose tiling
Rhombic Penrose tiling
In the dodecahedron and icosahedron
| Cartesian coordinates of the dodecahedron : | |
| (±1, ±1, ±1) | |
| (0, ±φ, ±1/φ) | |
| (±1/φ, 0, ±φ) | |
| (±φ, ±1/φ, 0) | |
| A nested cube inside the dodecahedron is represented with dotted lines. |
The regular dodecahedron and its dual polyhedron the icosahedron are Platonic solids whose dimensions are related to the golden ratio. An icosahedron is made of 


For a dodecahedron of side 






While for an icosahedron of side 



The volume and surface area of the dodecahedron can be expressed in terms of 


As well as for the icosahedron:

These geometric values can be calculated from their Cartesian coordinates, which also can be given using formulas involving 


Sets of three golden rectangles intersect perpendicularly inside dodecahedra and icosahedra, forming Borromean rings.[58][50] In dodecahedra, pairs of opposing vertices in golden rectangles meet the centers of pentagonal faces, and in icosahedra, they meet at its vertices. In all, the three golden rectangles contain 

A cube can be inscribed in a regular dodecahedron, with some of the diagonals of the pentagonal faces of the dodecahedron serving as the cube’s edges; therefore, the edge lengths are in the golden ratio. The cube’s volume is 



Other polyhedra are related to the dodecahedron and icosahedron or their symmetries, and therefore have corresponding relations to the golden ratio. These include the compound of five cubes, compound of five octahedra, compound of five tetrahedra, the compound of ten tetrahedra, rhombic triacontahedron, icosidodecahedron, truncated icosahedron, truncated dodecahedron, and rhombicosidodecahedron, rhombic enneacontahedron, and Kepler-Poinsot polyhedra, and rhombic hexecontahedron. In four dimensions, the dodecahedron and icosahedron appear as faces of the 120-cell and 600-cell, which again have dimensions related to the golden ratio.
Other properties
The golden ratio’s decimal expansion can be calculated via root-finding methods, such as Newton’s method or Halley’s method, on the equation 














The golden ratio and its conjugate 

Further, they are interchanged by the three maps 













In the complex plane, the fifth roots of unity 



![{textstyle mathbb {Z} [varphi ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c19ab3d8278828be7f591bad1dc4482e4aaac6d)
This also holds for the remaining tenth roots of unity satisfying 
For the gamma function 



When the golden ratio is used as the base of a numeral system (see golden ratio base, sometimes dubbed phinary or 
![{displaystyle mathbb {Z} [varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14f984c2710477c64fca0f16a71928134bdb8201)


The golden ratio also appears in hyperbolic geometry, as the maximum distance from a point on one side of an ideal triangle to the closer of the other two sides: this distance, the side length of the equilateral triangle formed by the points of tangency of a circle inscribed within the ideal triangle, is 
The golden ratio appears in the theory of modular functions as well. For 
Then
and
where 






and

Applications and observations
Architecture
The Swiss architect Le Corbusier, famous for his contributions to the modern international style, centered his design philosophy on systems of harmony and proportion. Le Corbusier’s faith in the mathematical order of the universe was closely bound to the golden ratio and the Fibonacci series, which he described as «rhythms apparent to the eye and clear in their relations with one another. And these rhythms are at the very root of human activities. They resound in man by an organic inevitability, the same fine inevitability which causes the tracing out of the Golden Section by children, old men, savages and the learned.»[66][67]
Le Corbusier explicitly used the golden ratio in his Modulor system for the scale of architectural proportion. He saw this system as a continuation of the long tradition of Vitruvius, Leonardo da Vinci’s «Vitruvian Man», the work of Leon Battista Alberti, and others who used the proportions of the human body to improve the appearance and function of architecture.
In addition to the golden ratio, Le Corbusier based the system on human measurements, Fibonacci numbers, and the double unit. He took suggestion of the golden ratio in human proportions to an extreme: he sectioned his model human body’s height at the navel with the two sections in golden ratio, then subdivided those sections in golden ratio at the knees and throat; he used these golden ratio proportions in the Modulor system. Le Corbusier’s 1927 Villa Stein in Garches exemplified the Modulor system’s application. The villa’s rectangular ground plan, elevation, and inner structure closely approximate golden rectangles.[68]
Another Swiss architect, Mario Botta, bases many of his designs on geometric figures. Several private houses he designed in Switzerland are composed of squares and circles, cubes and cylinders. In a house he designed in Origlio, the golden ratio is the proportion between the central section and the side sections of the house.[69]
Art
Leonardo da Vinci’s illustrations of polyhedra in Pacioli’s Divina proportione have led some to speculate that he incorporated the golden ratio in his paintings. But the suggestion that his Mona Lisa, for example, employs golden ratio proportions, is not supported by Leonardo’s own writings.[70] Similarly, although Leonardo’s Vitruvian Man is often shown in connection with the golden ratio, the proportions of the figure do not actually match it, and the text only mentions whole number ratios.[71][72]
Salvador Dalí, influenced by the works of Matila Ghyka,[73] explicitly used the golden ratio in his masterpiece, The Sacrament of the Last Supper. The dimensions of the canvas are a golden rectangle. A huge dodecahedron, in perspective so that edges appear in golden ratio to one another, is suspended above and behind Jesus and dominates the composition.[70][74]
A statistical study on 565 works of art of different great painters, performed in 1999, found that these artists had not used the golden ratio in the size of their canvases. The study concluded that the average ratio of the two sides of the paintings studied is 







Depiction of the proportions in a medieval manuscript. According to Jan Tschichold: «Page proportion 2:3. Margin proportions 1:1:2:3. Text area proportioned in the Golden Section.»[77]
Books and design
According to Jan Tschichold,
There was a time when deviations from the truly beautiful page proportions

and the Golden Section were rare. Many books produced between 1550 and 1770 show these proportions exactly, to within half a millimeter.[78]
According to some sources, the golden ratio is used in everyday design, for example in the proportions of playing cards, postcards, posters, light switch plates, and widescreen televisions.[79]
Flags
The aspect ratio (width to height ratio) of the flag of Togo was intended to be the golden ratio, according to its designer.[80]
Music
Ernő Lendvai analyzes Béla Bartók’s works as being based on two opposing systems, that of the golden ratio and the acoustic scale,[81] though other music scholars reject that analysis.[82] French composer Erik Satie used the golden ratio in several of his pieces, including Sonneries de la Rose+Croix. The golden ratio is also apparent in the organization of the sections in the music of Debussy’s Reflets dans l’eau (Reflections in Water), from Images (1st series, 1905), in which «the sequence of keys is marked out by the intervals 34, 21, 13 and 8, and the main climax sits at the phi position».[83]
The musicologist Roy Howat has observed that the formal boundaries of Debussy’s La Mer correspond exactly to the golden section.[84] Trezise finds the intrinsic evidence «remarkable», but cautions that no written or reported evidence suggests that Debussy consciously sought such proportions.[85]
Music theorists including Hans Zender and Heinz Bohlen have experimented with the 833 cents scale, a musical scale based on using the golden ratio as its fundamental musical interval. When measured in cents, a logarithmic scale for musical intervals, the golden ratio is approximately 833.09 cents.[86]
Nature
Johannes Kepler wrote that «the image of man and woman stems from the divine proportion. In my opinion, the propagation of plants and the progenitive acts of animals are in the same ratio».[87]
The psychologist Adolf Zeising noted that the golden ratio appeared in phyllotaxis and argued from these patterns in nature that the golden ratio was a universal law.[88] Zeising wrote in 1854 of a universal orthogenetic law of «striving for beauty and completeness in the realms of both nature and art».[89]
However, some have argued that many apparent manifestations of the golden ratio in nature, especially in regard to animal dimensions, are fictitious.[90]
Physics
The quasi-one-dimensional Ising ferromagnet CoNb2O6 (cobalt niobate) has 8 predicted excitation states (with E8 symmetry), that when probed with neutron scattering, showed its lowest two were in golden ratio. Specifically, these quantum phase transitions during spin excitation, which occur at near absolute zero temperature, showed pairs of kinks in its ordered-phase to spin-flips in its paramagnetic phase; revealing, just below its critical field, a spin dynamics with sharp modes at low energies approaching the golden mean.[91]
Optimization
There is no known general algorithm to arrange a given number of nodes evenly on a sphere, for any of several definitions of even distribution (see, for example, Thomson problem or Tammes problem). However, a useful approximation results from dividing the sphere into parallel bands of equal surface area and placing one node in each band at longitudes spaced by a golden section of the circle, i.e. 
The golden ratio is a critical element to golden-section search as well.
Disputed observations
Examples of disputed observations of the golden ratio include the following:
Nautilus shells are often erroneously claimed to be golden-proportioned.
- Specific proportions in the bodies of vertebrates (including humans) are often claimed to be in the golden ratio; for example the ratio of successive phalangeal and metacarpal bones (finger bones) has been said to approximate the golden ratio. There is a large variation in the real measures of these elements in specific individuals, however, and the proportion in question is often significantly different from the golden ratio.[93][94]
- The shells of mollusks such as the nautilus are often claimed to be in the golden ratio.[95] The growth of nautilus shells follows a logarithmic spiral, and it is sometimes erroneously claimed that any logarithmic spiral is related to the golden ratio,[96] or sometimes claimed that each new chamber is golden-proportioned relative to the previous one.[97] However, measurements of nautilus shells do not support this claim.[98]
- Historian John Man states that both the pages and text area of the Gutenberg Bible were «based on the golden section shape». However, according to his own measurements, the ratio of height to width of the pages is
[99]
- Studies by psychologists, starting with Gustav Fechner c. 1876,[100] have been devised to test the idea that the golden ratio plays a role in human perception of beauty. While Fechner found a preference for rectangle ratios centered on the golden ratio, later attempts to carefully test such a hypothesis have been, at best, inconclusive.[101][70]
- In investing, some practitioners of technical analysis use the golden ratio to indicate support of a price level, or resistance to price increases, of a stock or commodity; after significant price changes up or down, new support and resistance levels are supposedly found at or near prices related to the starting price via the golden ratio.[102] The use of the golden ratio in investing is also related to more complicated patterns described by Fibonacci numbers (e.g. Elliott wave principle and Fibonacci retracement). However, other market analysts have published analyses suggesting that these percentages and patterns are not supported by the data.[103]
Egyptian pyramids
The Great Pyramid of Giza (also known as the Pyramid of Cheops or Khufu) has been analyzed by pyramidologists as having a doubled Kepler triangle as its cross-section. If this theory were true, the golden ratio would describe the ratio of distances from the midpoint of one of the sides of the pyramid to its apex, and from the same midpoint to the center of the pyramid’s base. However, imprecision in measurement caused in part by the removal of the outer surface of the pyramid makes it impossible to distinguish this theory from other numerical theories of the proportions of the pyramid, based on pi or on whole-number ratios. The consensus of modern scholars is that this pyramid’s proportions are not based on the golden ratio, because such a basis would be inconsistent both with what is known about Egyptian mathematics from the time of construction of the pyramid, and with Egyptian theories of architecture and proportion used in their other works.[104]
The Parthenon
Many of the proportions of the Parthenon are alleged to exhibit the golden ratio, but this has largely been discredited.[105]
The Parthenon’s façade (c. 432 BC) as well as elements of its façade and elsewhere are said by some to be circumscribed by golden rectangles.[106] Other scholars deny that the Greeks had any aesthetic association with golden ratio. For example, Keith Devlin says, «Certainly, the oft repeated assertion that the Parthenon in Athens is based on the golden ratio is not supported by actual measurements. In fact, the entire story about the Greeks and golden ratio seems to be without foundation.»[107] Midhat J. Gazalé affirms that «It was not until Euclid … that the golden ratio’s mathematical properties were studied.»[108]
From measurements of 15 temples, 18 monumental tombs, 8 sarcophagi, and 58 grave stelae from the fifth century BC to the second century AD, one researcher concluded that the golden ratio was totally absent from Greek architecture of the classical fifth century BC, and almost absent during the following six centuries.[109]
Later sources like Vitruvius (first century BC) exclusively discuss proportions that can be expressed in whole numbers, i.e. commensurate as opposed to irrational proportions.
Modern art
The Section d’Or (‘Golden Section’) was a collective of painters, sculptors, poets and critics associated with Cubism and Orphism.[110] Active from 1911 to around 1914, they adopted the name both to highlight that Cubism represented the continuation of a grand tradition, rather than being an isolated movement, and in homage to the mathematical harmony associated with Georges Seurat.[111] (Several authors have claimed that Seurat employed the golden ratio in his paintings, but Seurat’s writings and paintings suggest that he employed simple whole-number ratios and any approximation of the golden ratio was coincidental.)[112] The Cubists observed in its harmonies, geometric structuring of motion and form, «the primacy of idea over nature», «an absolute scientific clarity of conception».[113] However, despite this general interest in mathematical harmony, whether the paintings featured in the celebrated 1912 Salon de la Section d’Or exhibition used the golden ratio in any compositions is more difficult to determine. Livio, for example, claims that they did not,[114] and Marcel Duchamp said as much in an interview.[115] On the other hand, an analysis suggests that Juan Gris made use of the golden ratio in composing works that were likely, but not definitively, shown at the exhibition.[115][116] Art historian Daniel Robbins has argued that in addition to referencing the mathematical term, the exhibition’s name also refers to the earlier Bandeaux d’Or group, with which Albert Gleizes and other former members of the Abbaye de Créteil had been involved.[117]
Piet Mondrian has been said to have used the golden section extensively in his geometrical paintings,[118] though other experts (including critic Yve-Alain Bois) have discredited these claims.[70][119]
See also
- List of works designed with the golden ratio
- Metallic mean
- Plastic number
- Sacred geometry
- Supergolden ratio
References
Explanatory footnotes
- ^ If the constraint on
and
each being greater than zero is lifted, then there are actually two solutions, one positive and one negative, to this equation.
is defined as the positive solution. The negative solution is
The sum of the two solutions is
, and the product of the two solutions is
.
- ^ Other names include the golden mean, golden section,[4] golden cut,[5] golden proportion, golden number,[6] medial section, and divine section.
- ^ Euclid, Elements, Book II, Proposition 11; Book IV, Propositions 10–11; Book VI, Proposition 30; Book XIII, Propositions 1–6, 8–11, 16–18.
- ^ «῎Ακρον καὶ μέσον λόγον εὐθεῖα τετμῆσθαι λέγεται, ὅταν ᾖ ὡς ἡ ὅλη πρὸς τὸ μεῖζον τμῆμα, οὕτως τὸ μεῖζον πρὸς τὸ ἔλαττὸν.»[18]
- ^ After Classical Greek sculptor Phidias (c. 490–430 BC);[33] Barr later wrote that he thought it unlikely that Phidias actually used the golden ratio.[34]
Citations
- ^ a b c Sloane, N. J. A. (ed.). «Sequence A001622 (Decimal expansion of golden ratio phi (or tau) = (1 + sqrt(5))/2)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^
Euclid. «Book 6, Definition 3». Elements. - ^
Pacioli, Luca (1509). De divina proportione. Venice: Luca Paganinem de Paganinus de Brescia (Antonio Capella). - ^ Livio 2002, pp. 3, 81.
- ^
Summerson, John (1963). Heavenly Mansions and Other Essays on Architecture. New York: W.W. Norton. p. 37.And the same applies in architecture, to the rectangles representing these and other ratios (e.g., the ‘golden cut’). The sole value of these ratios is that they are intellectually fruitful and suggest the rhythms of modular design.
- ^ Herz-Fischler 1998.
- ^ Herz-Fischler 1998, pp. 20–25.
- ^
Strogatz, Steven (2012-09-24). «Me, Myself, and Math: Proportion Control». The New York Times. - ^
Schielack, Vincent P. (1987). «The Fibonacci Sequence and the Golden Ratio». The Mathematics Teacher. 80 (5): 357–358. doi:10.5951/MT.80.5.0357. JSTOR 27965402. This source contains an elementary derivation of the golden ratio’s value. - ^
Peters, J. M. H. (1978). «An Approximate Relation between π and the Golden Ratio». The Mathematical Gazette. 62 (421): 197–198. doi:10.2307/3616690. - ^ Livio 2002, p. 6.
- ^ Livio 2002, p. 4: «… line division, which Euclid defined for … purely geometrical purposes …»
- ^ Livio 2002, pp. 7–8.
- ^ Livio 2002, pp. 4–5.
- ^ Livio 2002, p. 78.
- ^
Hemenway, Priya (2005). Divine Proportion: Phi In Art, Nature, and Science. New York: Sterling. pp. 20–21. - ^ Livio 2002, p. 3.
- ^
Euclid (2007). Euclid’s Elements of Geometry. Translated by Fitzpatrick, Richard. p. 156. ISBN 978-0615179841. - ^ Livio 2002, pp. 88–96.
- ^
Mackinnon, Nick (1993). «The Portrait of Fra Luca Pacioli». The Mathematical Gazette. 77 (479): 130–219. doi:10.2307/3619717. - ^ Livio 2002, pp. 131–132.
- ^
Baravalle, H. V. (1948). «The geometry of the pentagon and the golden section». Mathematics Teacher. 41: 22–31. doi:10.5951/MT.41.1.0022. - ^ Livio 2002, pp. 134–135.
- ^ Livio 2002, p. 141.
- ^
Schreiber, Peter (1995). «A Supplement to J. Shallit’s Paper ‘Origins of the Analysis of the Euclidean Algorithm’«. Historia Mathematica. 22 (4): 422–424. doi:10.1006/hmat.1995.1033. - ^ Livio 2002, pp. 151–152.
- ^
O’Connor, John J.; Robertson, Edmund F. (2001). «The Golden Ratio». MacTutor History of Mathematics archive. Retrieved 2007-09-18. - ^
Fink, Karl (1903). A Brief History of Mathematics. Translated by Beman, Wooster Woodruff; Smith, David Eugene (2nd ed.). Chicago: Open Court. p. 223. (Originally published as Geschichte der Elementar-Mathematik.) - ^
Beutelspacher, Albrecht; Petri, Bernhard (1996). «Fibonacci-Zahlen». Der Goldene Schnitt (in German). Vieweg+Teubner Verlag. pp. 87–98. doi:10.1007/978-3-322-85165-9_6. - ^ Herz-Fischler 1998, pp. 167–170.
- ^ Posamentier & Lehmann 2011, p. 8.
- ^ Posamentier & Lehmann 2011, p. 285.
- ^
Cook, Theodore Andrea (1914). The Curves of Life. London: Constable. p. 420. - ^
Barr, Mark (1929). «Parameters of beauty». Architecture (NY). Vol. 60. p. 325. Reprinted: «Parameters of beauty». Think. Vol. 10–11. IBM. 1944. - ^ Livio 2002, p. 5.
- ^
Gardner, Martin (2001). «7. Penrose Tiles». The Colossal Book of Mathematics. Norton. pp. 73–93. - ^
Livio 2002, pp. 203–209
Gratias, Denis; Quiquandon, Marianne (2019). «Discovery of quasicrystals: The early days». Comptes Rendus Physique. 20 (7–8): 803–816. doi:10.1016/j.crhy.2019.05.009.
Jaric, Marko V. (1989). Introduction to the Mathematics of Quasicrystals. Academic Press. p. x.Although at the time of the discovery of quasicrystals the theory of quasiperiodic functions had been known for nearly sixty years, it was the mathematics of aperiodic Penrose tilings, mostly developed by Nicolaas de Bruijn, that provided the major influence on the new field.
Goldman, Alan I.; Anderegg, James W.; Besser, Matthew F.; Chang, Sheng-Liang; Delaney, Drew W.; Jenks, Cynthia J.; Kramer, Matthew J.; Lograsso, Thomas A.; Lynch, David W.; McCallum, R. William; Shield, Jeffrey E.; Sordelet, Daniel J.; Thiel, Patricia A. (1996). «Quasicrystalline materials». American Scientist. 84 (3): 230–241. JSTOR 29775669. - ^
Martin, George E. (1998). Geometric Constructions. Springer. pp. 13–14. doi:10.1007/978-1-4612-0629-3. - ^
Hailperin, Max; Kaiser, Barbara K.; Knight, Karl W. (1999). Concrete Abstractions: An Introduction to Computer Science Using Scheme. Brooks/Cole. p. 63. - ^
Hardy, G. H.; Wright, E. M. (1960) [1938]. «§11.8. The measure of the closest approximations to an arbitrary irrational». An Introduction to the Theory of Numbers (4th ed.). Oxford University Press. pp. 163–164. - ^
Tattersall, James Joseph (1999). Elementary number theory in nine chapters. Cambridge University Press. p. 28. - ^
Parker, Matt (2014). Things to Make and Do in the Fourth Dimension. Farrar, Straus and Giroux. p. 284. - ^ King, S.; Beck, F.; Lüttge, U. (2004). «On the mystery of the golden angle in phyllotaxis». Plant, Cell and Environment. 27 (6): 685–695. doi:10.1111/j.1365-3040.2004.01185.x.
- ^
Odom, George; van de Craats, Jan (1986). «E3007: The golden ratio from an equilateral triangle and its circumcircle». Problems and solutions. The American Mathematical Monthly. 93 (7): 572. doi:10.2307/2323047. JSTOR 2323047. - ^
Busard, Hubert L. L. (1968). «L’algèbre au Moyen Âge : le «Liber mensurationum» d’Abû Bekr». Journal des Savants (in French and Latin). 1968 (2): 65–124. doi:10.3406/jds.1968.1175. See problem 51, reproduced on p. 98 - ^
Bruce, Ian (1994). «Another instance of the golden right triangle» (PDF). Fibonacci Quarterly. 32 (3): 232–233. - ^
Fletcher, Rachel (2006). «The golden section». Nexus Network Journal. 8 (1): 67–89. doi:10.1007/s00004-006-0004-z. - ^ a b c d
Loeb, Arthur (1992). «The Golden Triangle». Concepts & Images: Visual Mathematics. Birkhäuser. pp. 179–192. doi:10.1007/978-1-4612-0343-8_20. - ^ Posamentier & Lehmann 2011, p. 11.
- ^ a b
Burger, Edward B.; Starbird, Michael P. (2005) [2000]. The Heart of Mathematics: An Invitation to Effective Thinking (2nd ed.). Springer. p. 382. - ^ a b
Grünbaum, Branko (1996). «A new rhombic hexecontahedron» (PDF). Geombinatorics. 6 (1): 15–18. - ^
Senechal, Marjorie (2006). «Donald and the golden rhombohedra». In Davis, Chandler; Ellers, Erich W. (eds.). The Coxeter Legacy. American Mathematical Society. pp. 159–177. ISBN 0-8218-3722-2. - ^
Miller, William (1996). «Pentagons and Golden Triangles». Mathematics in School. 25 (4): 2–4. JSTOR 30216571. - ^ a b c d
Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. pp. 537–547. - ^
Penrose, Roger (1978). «Pentaplexity». Eureka. Vol. 39. p. 32. (original PDF) - ^
Frettlöh, D.; Harriss, E.; Gähler, F. «Robinson Triangle». Tilings Encyclopedia.Clason, Robert G (1994). «A family of golden triangle tile patterns». The Mathematical Gazette. 78 (482): 130–148. doi:10.2307/3618569.
- ^ a b Livio (2002, pp. 70–72)
- ^
Gunn, Charles; Sullivan, John M. (2008). «The Borromean Rings: A video about the New IMU logo». In Sarhangi, Reza; Séquin, Carlo H. (eds.). Proceedings of Bridges 2008. Leeuwarden, the Netherlands. Tarquin Publications. pp. 63–70.; Video at «The Borromean Rings: A new logo for the IMU». International Mathematical Union. - ^
Hume, Alfred (1900). «Some propositions on the regular dodecahedron». The American Mathematical Monthly. 7 (12): 293–295. doi:10.2307/2969130. - ^
Coxeter, H.S.M.; du Val, Patrick; Flather, H.T.; Petrie, J.F. (1938). The Fifty-Nine Icosahedra. Vol. 6. University of Toronto Studies. p. 4.Just as a tetrahedron can be inscribed in a cube, so a cube can be inscribed in a dodecahedron. By reciprocation, this leads to an octahedron circumscribed about an icosahedron. In fact, each of the twelve vertices of the icosahedron divides an edge of the octahedron according to the «golden section.
- ^
Muller, J. M. (2006). Elementary functions : algorithms and implementation (2nd ed.). Boston: Birkhäuser. p. 93. ISBN 978-0817643720. - ^
Yee, Alexander J. (2021-03-13). «Records Set by y-cruncher». numberword.org. Two independent computations done by Clifford Spielman. - ^
Horocycles exinscrits : une propriété hyperbolique remarquable, cabri.net, retrieved 2009-07-21. - ^
Berndt, Bruce C.; Chan, Heng Huat; Huang, Sen-Shan; Kang, Soon-Yi; Sohn, Jaebum; Son, Seung Hwan (1999). «The Rogers–Ramanujan Continued Fraction» (PDF). Journal of Computational and Applied Mathematics. 105 (1–2): 9–24. doi:10.1016/S0377-0427(99)00033-3. - ^
Duffin, Richard J. (1978). «Algorithms for localizing roots of a polynomial and the Pisot Vijayaraghavan numbers». Pacific Journal of Mathematics. 74 (1): 47–56. doi:10.2140/pjm.1978.74.47. - ^ Le Corbusier, The Modulor, p. 25, as cited in
Padovan, Richard (1999). Proportion: Science, Philosophy, Architecture. Taylor & Francis. p. 316. doi:10.4324/9780203477465. - ^
Frings, Marcus (2002). «The Golden Section in Architectural Theory». Nexus Network Journal. 4 (1): 9–32. doi:10.1007/s00004-001-0002-0. - ^ Le Corbusier, The Modulor, p. 35, as cited in
Padovan, Richard (1999). Proportion: Science, Philosophy, Architecture. Taylor & Francis. p. 320. doi:10.4324/9780203477465.Both the paintings and the architectural designs make use of the golden section
- ^
Urwin, Simon (2003). Analysing Architecture (2nd ed.). Routledge. pp. 154–155. - ^ a b c d
Livio, Mario (2002). «The golden ratio and aesthetics». Plus Magazine. Retrieved November 26, 2018. - ^
Devlin, Keith (2007). «The Myth That Will Not Go Away». Retrieved September 26, 2013.Part of the process of becoming a mathematics writer is, it appears, learning that you cannot refer to the golden ratio without following the first mention by a phrase that goes something like ‘which the ancient Greeks and others believed to have divine and mystical properties.’ Almost as compulsive is the urge to add a second factoid along the lines of ‘Leonardo Da Vinci believed that the human form displays the golden ratio.’ There is not a shred of evidence to back up either claim, and every reason to assume they are both false. Yet both claims, along with various others in a similar vein, live on.
- ^
Simanek, Donald E. «Fibonacci Flim-Flam». Archived from the original on January 9, 2010. Retrieved April 9, 2013. - ^
Salvador Dalí (2008). The Dali Dimension: Decoding the Mind of a Genius (DVD). Media 3.14-TVC-FGSD-IRL-AVRO. - ^
Hunt, Carla Herndon; Gilkey, Susan Nicodemus (1998). Teaching Mathematics in the Block. pp. 44, 47. ISBN 1-883001-51-X. - ^
Olariu, Agata (1999). «Golden Section and the Art of Painting». arXiv:physics/9908036. - ^
Tosto, Pablo (1969). La composición áurea en las artes plásticas [The golden composition in the plastic arts] (in Spanish). Hachette. pp. 134–144. - ^
Tschichold, Jan (1991). The Form of the Book. Hartley & Marks. p. 43 Fig 4. ISBN 0-88179-116-4.Framework of ideal proportions in a medieval manuscript without multiple columns. Determined by Jan Tschichold 1953. Page proportion 2:3. margin proportions 1:1:2:3, Text area proportioned in the Golden Section. The lower outer corner of the text area is fixed by a diagonal as well.
- ^
Tschichold, Jan (1991). The Form of the Book. Hartley & Marks. pp. 27–28. ISBN 0-88179-116-4. - ^
Jones, Ronald (1971). «The golden section: A most remarkable measure». The Structurist. 11: 44–52.Who would suspect, for example, that the switch plate for single light switches are standardized in terms of a Golden Rectangle?
Johnson, Art (1999). Famous problems and their mathematicians. Teacher Ideas Press. p. 45.
The Golden Ratio is a standard feature of many modern designs, from postcards and credit cards to posters and light-switch plates.
Stakhov, Alexey P.; Olsen, Scott (2009). «§1.4.1 A Golden Rectangle with a Side Ratio of τ«. The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science. World Scientific. p. 20–21.
A credit card has a form of the golden rectangle
Cox, Simon (2004). Cracking the Da Vinci Code. Barnes & Noble. p. 62.
The Golden Ratio also crops up in some very unlikely places: widescreen televisions, postcards, credit cards and photographs all commonly conform to its proportions.
- ^ Posamentier & Lehmann 2011, chapter 4, footnote 12: «The Togo flag was designed by the artist Paul Ahyi (1930–2010), who claims to have attempted to have the flag constructed in the shape of a golden rectangle».
- ^
Lendvai, Ernő (1971). Béla Bartók: An Analysis of His Music. London: Kahn and Averill. - ^ Livio 2002, p. 190.
- ^
Smith, Peter F. (2003). The Dynamics of Delight: Architecture and Aesthetics. Routledge. p. 83. - ^
Howat, Roy (1983). «1. Proportional structure and the Golden Section». Debussy in Proportion: A Musical Analysis. Cambridge University Press. pp. 1–10. - ^
Trezise, Simon (1994). Debussy: La Mer. Cambridge University Press. p. 53. - ^
Mongoven, Casey (2010). «A style of music characterized by Fibonacci and the golden ratio» (PDF). Congressus Numerantium. 201: 127–138.Hasegawa, Robert (2011). «Gegenstrebige Harmonik in the Music of Hans Zender». Perspectives of New Music. Project Muse. 49 (1): 207–234. doi:10.1353/pnm.2011.0000. JSTOR 10.7757/persnewmusi.49.1.0207.
Smethurst, Reilly (2016). «Two Non-Octave Tunings by Heinz Bohlen: A Practical Proposal». In Torrence, Eve; et al. (eds.). Proceedings of Bridges 2016. Jyväskylä, Finland. Tessellations Publishing. pp. 519–522.
- ^ Livio 2002, p. 154.
- ^
Padovan, Richard (1999). Proportion: Science, Philosophy, Architecture. Taylor & Francis. pp. 305–306. doi:10.4324/9780203477465.Padovan, Richard (2002). «Proportion: Science, Philosophy, Architecture». Nexus Network Journal. 4 (1): 113–122. doi:10.1007/s00004-001-0008-7.
- ^
Zeising, Adolf (1854). «Einleitung [preface]». Neue Lehre von den Proportionen des menschlichen Körpers [New doctrine of the proportions of the human body] (in German). Weigel. pp. 1–10. - ^
Pommersheim, James E.; Marks, Tim K.; Flapan, Erica L., eds. (2010). Number Theory: A Lively Introduction with Proofs, Applications, and Stories. Wiley. p. 82. - ^
Coldea, R.; Tennant, D.A.; Wheeler, E.M.; Wawrzynksa, E.; Prabhakaran, D.; Telling, M.; Habicht, K.; Smeibidl, P.; Keifer, K. (2010). «Quantum Criticality in an Ising Chain: Experimental Evidence for Emergent E8 Symmetry». Science. 327 (5962): 177–180. arXiv:1103.3694. doi:10.1126/science.1180085. - ^
«A Disco Ball in Space». NASA. 2001-10-09. Retrieved 2007-04-16. - ^
Pheasant, Stephen (1986). Bodyspace. Taylor & Francis. - ^
van Laack, Walter (2001). A Better History Of Our World: Volume 1 The Universe. Aachen: van Laach. - ^
Dunlap, Richard A. (1997). The Golden Ratio and Fibonacci Numbers. World Scientific. p. 130. - ^
Falbo, Clement (March 2005). «The golden ratio—a contrary viewpoint». The College Mathematics Journal. 36 (2): 123–134. doi:10.1080/07468342.2005.11922119. - ^
Moscovich, Ivan (2004). The Hinged Square & Other Puzzles. New York: Sterling. p. 122. - ^
Peterson, Ivars (1 April 2005). «Sea shell spirals». Science News. Archived from the original on 3 October 2012. Retrieved 10 November 2008. - ^
Man, John (2002). Gutenberg: How One Man Remade the World with Word. Wiley. pp. 166–167.The half-folio page (30.7 × 44.5 cm) was made up of two rectangles—the whole page and its text area—based on the so called ‘golden section’, which specifies a crucial relationship between short and long sides, and produces an irrational number, as pi is, but is a ratio of about 5:8.
- ^
Fechner, Gustav (1876). Vorschule der Ästhetik [Preschool of Aesthetics] (in German). Leipzig: Breitkopf & Härtel. pp. 190–202. - ^ Livio 2002, p. 7.
- ^
Osler, Carol (2000). «Support for Resistance: Technical Analysis and Intraday Exchange Rates» (PDF). Federal Reserve Bank of New York Economic Policy Review. 6 (2): 53–68. Archived (PDF) from the original on 2007-05-12.38.2 percent and 61.8 percent retracements of recent rises or declines are common,
- ^
Batchelor, Roy; Ramyar, Richard (2005). Magic numbers in the Dow (Report). Cass Business School. pp. 13, 31.
Popular press summaries can be found in:
Stevenson, Tom (2006-04-10). «Not since the ‘big is beautiful’ days have giants looked better». The Daily Telegraph.
«Technical failure». The Economist. 2006-09-23. - ^
Herz-Fischler, Roger (2000). The Shape of the Great Pyramid. Wilfrid Laurier University Press. ISBN 0-88920-324-5. The entire book surveys many alternative theories for this pyramid’s shape. See Chapter 11, «Kepler triangle theory», pp. 80–91, for material specific to the Kepler triangle, and p. 166 for the conclusion that the Kepler triangle theory can be eliminated by the principle that «A theory must correspond to a level of mathematics consistent with what was known to the ancient Egyptians.» See note 3, p. 229, for the history of Kepler’s work with this triangle.Rossi, Corinna (2004). Architecture and Mathematics in Ancient Egypt. Cambridge University Press. pp. 67–68.
there is no direct evidence in any ancient Egyptian written mathematical source of any arithmetic calculation or geometrical construction which could be classified as the Golden Section … convergence to
; see also extensive discussion of multiple alternative theories for the shape of the pyramid and other Egyptian architecture, pp. 7–56, and
itself as a number, do not fit with the extant Middle Kingdom mathematical sources
Rossi, Corinna; Tout, Christopher A. (2002). «Were the Fibonacci series and the Golden Section known in ancient Egypt?». Historia Mathematica. 29 (2): 101–113. doi:10.1006/hmat.2001.2334.
Markowsky, George (1992). «Misconceptions about the Golden Ratio» (PDF). The College Mathematics Journal. Mathematical Association of America. 23 (1): 2–19. doi:10.2307/2686193. Retrieved 2012-06-29.
It does not appear that the Egyptians even knew of the existence of
much less incorporated it in their buildings
- ^ Livio 2002, pp. 74–75.
- ^
Van Mersbergen, Audrey M. (1998). «Rhetorical Prototypes in Architecture: Measuring the Acropolis with a Philosophical Polemic». Communication Quarterly. 46 (2): 194–213. doi:10.1080/01463379809370095. - ^
Devlin, Keith J. (2005). The Math Instinct. New York: Thunder’s Mouth Press. p. 108. - ^
Gazalé, Midhat J. (1999). Gnomon: From Pharaohs to Fractals. Princeton. p. 125. - ^
Foutakis, Patrice (2014). «Did the Greeks Build According to the Golden Ratio?». Cambridge Archaeological Journal. 24 (1): 71–86. doi:10.1017/S0959774314000201. - ^
Le Salon de la Section d’Or, October 1912, Mediation Centre Pompidou - ^
Jeunes Peintres ne vous frappez pas !, La Section d’Or: Numéro spécial consacré à l’Exposition de la «Section d’Or», première année, n° 1, 9 octobre 1912, pp. 1–7 Archived 2020-10-30 at the Wayback Machine, Bibliothèque Kandinsky - ^
Herz-Fischler, Roger (1983). «An Examination of Claims Concerning Seurat and the Golden Number» (PDF). Gazette des Beaux-Arts. 101: 109–112. - ^
Herbert, Robert (1968). Neo-Impressionism. Guggenheim Foundation.[page needed] - ^ Livio 2002, p. 169.
- ^ a b
Camfield, William A. (March 1965). «Juan Gris and the golden section». The Art Bulletin. 47 (1): 128–134. doi:10.1080/00043079.1965.10788819. - ^
Green, Christopher (1992). Juan Gris. Yale. pp. 37–38.Cottington, David (2004). Cubism and Its Histories. Manchester University Press. p. 112, 142.
- ^
Allard, Roger (June 1911). «Sur quelques peintres». Les Marches du Sud-Ouest: 57–64.
Reprinted in
Antliff, Mark; Leighten, Patricia, eds. (2008). A Cubism Reader, Documents and Criticism, 1906–1914. The University of Chicago Press. pp. 178–191. - ^
Bouleau, Charles (1963). The Painter’s Secret Geometry: A Study of Composition in Art. Harcourt, Brace & World. pp. 247–248. - ^ Livio 2002, pp. 177–178.
Works cited
- Herz-Fischler, Roger (1998) [1987]. A Mathematical History of the Golden Number. Dover. ISBN 9780486400075. (Originally titled A Mathematical History of Division in Extreme and Mean Ratio.)
- Livio, Mario (2002). The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number. New York: Broadway Books. ISBN 9780767908153.
- Posamentier, Alfred S.; Lehmann, Ingmar (2011). The Glorious Golden Ratio. Prometheus Books. ISBN 9-781-61614-424-1.
Further reading
- Doczi, György (1981). The Power of Limits: Proportional Harmonies in Nature, Art, and Architecture. Boston: Shambhala.
- Hargittai, István, ed. (1992). Fivefold Symmetry. World Scientific. ISBN 9789810206000.
- Huntley, H. E. (1970). The Divine Proportion: A Study in Mathematical Beauty. New York: Dover. ISBN 978-0-486-22254-7.
- Schaaf, William L., ed. (1967). The Golden Measure (PDF). California School Mathematics Study Group Reprint Series. Stanford University. Archived (PDF) from the original on 2015-04-25.
- Scimone, Aldo (1997). La Sezione Aurea. Storia culturale di un leitmotiv della Matematica. Palermo: Sigma Edizioni. ISBN 978-88-7231-025-0.
- Walser, Hans (2001) [Der Goldene Schnitt 1993]. The Golden Section. Peter Hilton trans. Washington, DC: The Mathematical Association of America. ISBN 978-0-88385-534-8.
External links
- «Golden ratio». Encyclopedia of Mathematics. EMS Press. 2001 [1994].
- «Golden Section» by Michael Schreiber, Wolfram Demonstrations Project, 2007.
- Weisstein, Eric W. «Golden Ratio». MathWorld.
- Knott, Ron. «The Golden section ratio: Phi». Information and activities by a mathematics professor.
- The Myth That Will Not Go Away, by Keith Devlin, addressing multiple allegations about the use of the golden ratio in culture.
- Spurious golden spirals collected by Randall Munroe
- YouTube lecture on Zeno’s mice problem and logarithmic spirals
«Полная симметрия докучает, а изящное разнообразие красит и тешит вкус» В.И. Даль.
ИСТОРИЯ ЗОЛОТОЙ ПРОПОРЦИИ И ПЕРЕХОД К ПРИРОДОПОДОБНЫМ ТЕХНОЛОГИЯМ
ЧАСТЬ ПЕРВАЯ — ИСТОРИЯ ЗОЛОТОЙ ПРОПОРЦИИ
Хроника истории описывает череду прецедентов открытий и их применения, а также множество заблуждений и ошибок, основанных на таком феномене всех времён, как Золотая Пропорция.
Ее называют по-разному: Золотым Делением, Золотой Пропорцией, Золотым Сечением, Божественной мерой Красоты и Гармонии.
Все ли эти названия выражают один смысл? Правильно ли описана суть явления? О чем же повествует история и к какому цивилизационному порогу она нас привела?
Рассмотрим историю по принципу Золотой Пропорции и возьмём только меньшую часть из целого в последовательности открытий.
Посмотрим на несколько примеров, как Золотая Пропорция дарила человечеству шедевры прозрений. В разные эпохи, разные народы, исследователи, учёные находили свои феноменальные особенности этой меры…
• Древние цивилизации оставили следы употребления Золотой Пропорции, например, в Индии, Египте, а так же шумеры, европейцы, американские племена, древние славяне…
• Впервые о Золотом Сечении упоминается в книгах III-II века до н.э., хотя задолго до этого Пифагор уже говорил о Золотом Делении, но не записывал, об этом написали позже его последователи.
• Золотое Деление, описанное в «Элементах Эвклида» 2300 лет назад, представлено двумя объектами, которые находятся в Золотой Пропорции относительно друг друга.
• Фибоначчи оставил в истории правило шага Золотой Пропорции в целых числах, он создал последовательность чисел, известную как Ряд Фибоначчи.
• Первое научное объяснение прозвучало от монаха Луки Пачоли в 1509 году, который писал о Золотом Сечении, как о Божественном Триединстве.
• Леонардо да Винчи выявил соотношения сторон прямоугольников в Золотом Сечении, подробно разобрал канонические пропорции человеческого тела, исходя из среднего роста человека 1,75 метра, подарил миру Витрувианского человека. Применил Золотое Сечение в инженерии, различных видах искусств, в частности живописи, оставив одни из самых гениальных произведений в истории человечества.
• Андреа Палладио заложил основу классицизма в архитектуре, став на века одним из самых влиятельных архитекторов в истории, главным маяком и отцом для поколений архитекторов и изобретателем универсального архитектурного языка логической пропорциональности и гармонии.

• Иоганн Кеплер, опираясь на выводы Пифагора, подарил миру открытие в отношениях чисел и пропорций, описал Треугольник Кеплера, ввёл понятие: «среднее гармоническое».
«В геометрии существует два сокровища: одно из них — теорема Пифагора, другое — разделение линии в Золотой Пропорции. Первое мы можем сравнить с массой золота, второе мы можем назвать драгоценным камнем» Иоганн Кеплер.
• Творчество Пушкина исследовали, и оказалось, что есть произведения, в которых прослеживается ряд Фибоначчи.
• В 1855 году Адольф Цейзинг довёл до Абсолюта пропорции Золотого Сечения, сделав их универсальными для всех явлений окружающего мира и определил, что Золотое Сечение выражает Среднестатистический Закон.
• И.В. Жолтовский, академик архитектуры, изучал учение Андреа Палладио, привёз четыре его книги в Россию и перевел, развил учение и стал основоположником неоклассицизма.
Он считал, что если в архитектуре брать и выделять три части из шага Золотой Пропорции, то всегда проявится красота и жизненность, что он наглядно продемонстрировал на первом здании МГУ на Моховой улице и ещё на многих известных и красивейших зданиях Москвы.
• Архитектор Ле Корбюзье создал собственную Шкалу Гармоничных Пропорций – Модулор Ле Карбюзье, повлиявшую на эстетику архитектуры XX века. Модулор используют все последующие поколения архитекторов, начиная со студенческой скамьи.
Ле Карбюзье построил, с использованием правила Золотой Пропорции, город Чиндигарх в Индии, который стал объектом всемирного наследия ЮНЕСКО, и доходы на душу населения, в этом городе, самые высокие в Индии.

• Искусствовед Ф.В. Ковалёв обнаружил соответствие Золотой Пропорции расположение деталей и предметов в картине Николая Ге.
• И.Ш. Шевелёв М.А. Марутаев И.П. Шмелёв попытались теоретически обосновать феномен Золотого Сечения, в котором авторы видят одну из универсальных закономерностей Природы: в архитектуре, музыке, психологии восприятия и формообразования живой природы, а также в таблице Менделеева, планетарных расстояниях, макро и микромире…
• А.Ф. Черняев направлял свои исследования в различные научные отрасли: Золотые Пропорции, механику, геометрию, гравитацию, древнерусские сажени (несколько размеров из Природных шагов Золотой Пропорции в человеческом теле). Анатолий Черняев многогранный исследователь, мыслитель, автор популярных книг и статей, известный своим неординарным подходом к новым идеям и неожиданным взглядам на различные явления.
• Учёный Эдуард Сороко обратил внимание на формы Золотых Делений в Природе, на одну из самых известных форм — спираль, хотя надо признать, что задолго до этого Архимед на основе формы спирали вывел уравнение, а Гёте отметил тяготение Природы к спиральным формам.
• А.С. Харитонов к.ф.-м.н., исследователь проявлений Золотой Пропорции, лектор и неутомимый пропагандист, говорит о противоречии взглядов, он доказывает ошибочность второго закона термодинамики, по теории которого природа должна эволюционировать к максимальному хаосу, а согласно же математике Природной гармонии — мир стремится именно к этой самой гармонии. Разрешение данного противоречия затрагивает основы математики, физики, биологии и социологии, открывает новые горизонты для философии.
Анатолий Харитонов утверждает, что пришло время пересмотреть многие подходы к современной математике, которые он считает ошибочными с точки зрения проявлений Золотой Пропорции в Природе.
• В.И. Говоров рассуждая о Тайне Божественной Пропорции и Золотой Пропорции, считает их похожими, но разными по сути своих проявлений по горизонтали и вертикали. Термин Золотое Сечение он считает вообще ошибочным по своей сути и отказывает в праве на его употребление.
• А.В. Осипов объяснил причину и следствие проявлений системы Триединства в Природе, а также показал то, как Золотая Пропорция использовалась различными цивилизациями. Обосновал и спрогнозировал Новую Эпоху с осознанным применением Природоподобных Технологий в гуманитарной и технологических сферах.
Аркадий Осипов отработал Методы практики применения проявлений Золотой Пропорции в Природоподобных Технологиях. Применил и проверил эти методики: в гуманитарной сфере — на выборах губернатора Алтайского Края в 2004 году, в инженерии — спроектировал со своей частной научной группой «идеальные», с точки зрения Природоподобия, домовые хозяйства, фермы, храмы, разработал концепцию посёлков, жилищных комплексов, сверхвысоких небоскрёбов и городов будущего.
Справедливости ради, надо отметить, что в данном списке должно быть гораздо больше имён любителей и исследователей Золотой Пропорции. Многие люди на всём протяжении истории делали серьёзные открытия, но сохранили их в тайне, одни масоны и различные тайные общества чего стоят. Много пытливых умов и учёных современности занимаются исследованиями для себя, некоторые скромны или засекречены, так как их открытия используются в оборонном секторе и за этими открытиями ведётся «охота» ведущих разведок мира.
Важно подчеркнуть, что основные открытия в области проявлений принципа Триединства еще впереди, придут поколения исследователей, учёных, которые продвинутся много дальше и точнее в этой бесконечной, как само мироздание теме. В историческом смысле, можно сказать, что список исследователей комплекса проявлений Золотой Пропорции, как элемента Природоподобных Технологий, только начался…
ЧАСТЬ ВТОРАЯ
ПЕРЕХОД К ПРИРОДОПОДОБНЫМ ТЕХНОЛОГИЯМ И МЕТОД АРКАДИЯ ОСИПОВА
Рассмотрим более детально феномен появления в открытом доступе работ нашего современника, экономиста Аркадия Владимировича Осипова. Он систематизировал и объяснил использование проявлений Золотой Пропорции предыдущими цивилизациями и современной наукой, объяснил происхождение некоторых особенностей Природоподобия и показательно применил на практике выработанные им методики Природоподобных Технологий, причём, в двух сферах — гуманитарной и техногенной, а также показал природу ошибок и заблуждений иногда встречающихся у исследователей Золотой Пропорции.
Он утверждает, что обещанная пророками Золотая Эпоха, а представителями науки и политики — Новая Эра, наступает прямо сейчас. Мнения мистиков (предсказания о Трёх Саи Аватарах в Индии), представителей религий (особенно пророков раннего христианства), науки (МГУ, НИЦ Курчатовский Институт — президент М.В. Ковальчук) и даже политики (В.В. Путин в 2015 году на Генеральной Ассамблее ООН) сошлись в одной точке.
А.В. Осипов говорит о проявлениях Золотой Пропорции как о раскрытии универсального принципа Троицы (Триединства) в материальном мире, как о Природных Технологиях, которые становятся при осознанном применении Стандартов Природы — Природоподобными Технологиями. Освоение Природоподобных Технологий приводит человечество к созданию нового гуманитарного уклада и одновременно новой техносферы и, соответственно, к Новой Эпохе осознанного использования проявлений Принципа Триединства.
Аркадий Осипов рассматривает две линейки Золотой Пропорции, которые всегда присутствуют в Природной инженерии, в дуальной совокупности (системы независимые, но дополняющие друг друга) с фактором регулятора пространства. Этот фактор называется — Цветок Жизни или Цветок Пространства (круг с определёнными особенностями, описанный вокруг человека с вытянутой вверх рукой).
Свойства этого, «незримо присутствующего», круга выявляют и объясняют принцип сборки частей в целое — принцип, который в свою очередь, влияет на специфику образования ростовых групп в живой Природе. Дело в том, что части в целое собираются только на определённом Природном шаге Золотой Пропорции и обязательно есть промежуточные шаги, где есть части, но нет целого.
Осипов предупреждает, что употребление некоторых универсальных формул проявления Золотой Пропорции, а так же сложение саженей, при Природоподобном конструировании, в отдельных случаях, может иметь право на жизнь, а в некоторых случаях, без учёта сопутствующих факторов, может привести к ошибочным результатам, к псевдо-природным проявлениям, которые в живой Природе отсутствуют.
По Осипову, размер в Природе имеет ключевое значение, он может быть «переменным» — раздражающим, толкающим систему к изменениям (размер, который Природа старается проскочить), или «постоянным» — несущим удовлетворение и жизнеспособность (размер, который Природа старается зафиксировать). Наша жизнь это чередование этих проявлений.
Размеры Природного субъекта рождают соответствующие площади, объёмы, энергии, которые несут человеку и окружающим представителям биоценоза особые состояния – «переменные» или «постоянные», которые, в итоге, влияют на результаты естественного отбора. Учитывая эти особенности Природы, естественный отбор теперь можно проходить на стадии проектирования, получая абсолютную Природную гармонию и жизнеспособность у рукотворных изделий. Взял верные, с точки зрения Природоподобия, размеры и пропорции — получил весь комплекс гармонии.
По большому счёту, размерность и психология, накрепко связанные, переплетённые между собой явления. В гуманитарном смысле, А.В. Осипов называет проявления Золотой Пропорции – «неравновесным равновесием» и правилом Природных доминант, акцентов и предпочтений. Он показывает почему, в психологическом смысле, надо стать меньшим, чтобы быть большим. Этот принцип программно регулирует поведенческую структуру с причинно-следственной связью у всего живого и, в первую очередь, у человека. Этот же фактор заложен в основу всех религиозных толкований, духовных культур и подтверждает потребность в духовности для гармоничной реализации личности.
Именно эта особенность проявлений Природы, в причинно-следственной деятельности нашего сознания, позволит объяснить историю с войнами и их последствиями, бывшими и будущими развалами империй, уравновесит и оптимизирует экономику, в том числе развитие западных и восточных регионов, сбалансирует расслоение общества, поставит на здоровую справедливую основу систему выборов. Данное технологическое правило причинно-следственности доминант и акцентов способно гармонизировать государственное, политическое, социальное, идеологическое устройство, духовную сферу и, что особенно важно, поможет раскрыть потенциал личности и семьи. Что проще, когда знаешь причину и следствие?
Среда обитания, по умолчанию, оказывает влияние на развитие личности и развитие социума. Современный человек и его мышление, социальные, политические составляющие, также как окружающая рукотворная среда, нуждаются в положительных корректировках, которые теперь могут подсказать нам Природоподобные Технологии.
Показательным примером применения общественно-политических технологических корректировок может служить организация выборов губернатора Алтайского Края в 2004 году, когда были минимальные возможности победить существующего губернатора.
Добиться преимущества удалось рядом приёмов, выравниванием и уравновешиванием организационных провалов работы местной власти. В данном случае, одним из таких приёмов было точечное смещение доли участия представителей общественности на выборах, объединение их в Совет общественных движений края. После выборов этот Совет был преобразован в Общественную Палату за полгода до объявления о создании Общественных Палат президентом РФ В.В. Путиным.
Верно скорректированные акценты, с точки зрения Природоподобных Технологий, способствовали тому, что общественное движение неожиданно набрало силу и по признанию руководителя профильного комитета Государственной Думы и руководства Сибирского Федерального Округа стало самым активным в России.
Об инженерии: «Интересно, что в настоящее время, мы уже способны принципиально оптимизировать всю техносферу. Человек сможет чувствовать себя так благотворно в урбанистической среде, как на Природе, поскольку рукотворная среда будет создана по тем же принципам, как, например, идеально сбалансированный природный оазис с эффектом процветания и биоценозной гармонии» А. Осипов.
Осипов систематизировал проявления Золотой Пропорции, упростил подходы к осмыслению и практику применения Природоподобных Технологий для научных исследований, для повседневного быта, вплоть до освоения и использования детьми и домохозяйками. Начал создавать буквари Природоподобных Технологий, как для гуманитарной сферы (с проявлениями социально-психологических основ и индивидуальных поведенческих норм), так и для рукотворной инженерии.
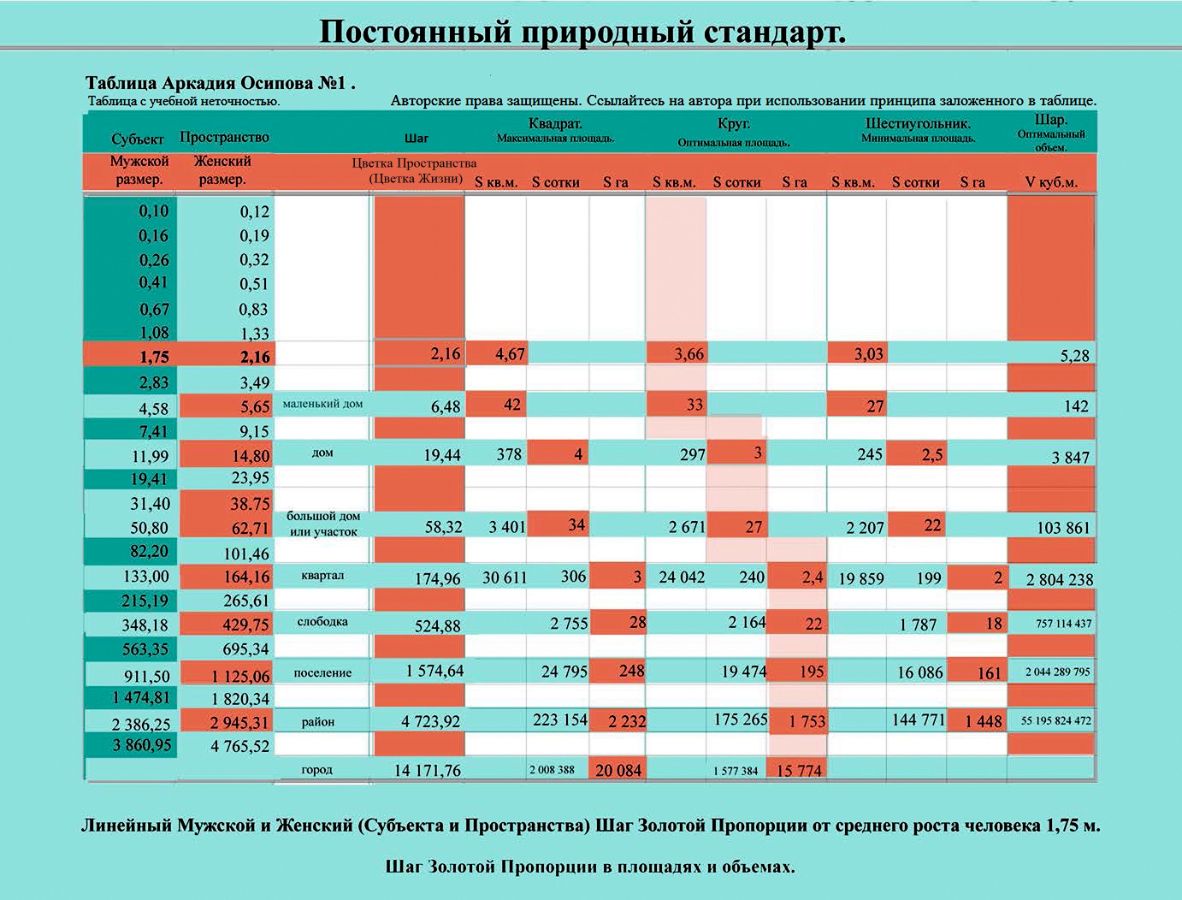
Метод Аркадия Осипова заключается в способах применения Природоподобных Технологий и позволяет, например, спроектировать идеальный дом мечты так, как бы его «вырастила» Природа, если бы в ДНК были заложены все утилитарные потребности заказчика. Созданными по принципам Природоподобия могут быть домовое хозяйство, квартира, предметы быта. Примером, из уже сделанного и проявившего свои особые качества, может служить улей для пчёл, печь, зеркало, нож, кухонная утварь, спальное и рабочее место — со свойствами Природной гармонии.
Несколько вариантов домов, домовых хозяйств, агроферм Природного Земледелия, с подобным универсальным подходом, а также варианты домов под конкретного человека и его семью, были спроектированы Осиповым и частной научной группой архитекторов из Витебска и Высшей Школы Средового Дизайна МАРХИ. Кроме того, были спроектированы образцы гармонии — храмы и храмовые комплексы, разработаны концепции жилых комплексов, посёлков, высотных зданий и сверхвысоких небоскрёбов, городов будущего.
Технологии Природы нужны людям в малом бытовом смысле, в реализации серьёзных проектов, в том числе инфраструктурных, в первую очередь, из соображений безопасности. А.В. Осипов в своих работах раскрывает, почему сомнительно, в финансовом смысле, вкладываться, создавая небоскрёбы без Природоподобных Технологий, и почему самый высокий небоскрёб можно строить только по принципам Природоподобия, которые дают возможность, в инженерном смысле, безопасно выйти за километровую высотность. Небоскрёбы в ОАЭ и Саудовской Аравии, в этом смысле, априори создаются с отклонениями от Природоподобия и с ошибками. Города будущего создавать без Природоподобных Технологий, значит, как минимум, закладывать риск убыточности, отсутствие возможности для окупаемости технологических новшеств.
Причина — опасность «переменных» отталкивающих состояний и шлейфа сопутствующих отрицательных факторов, которые автоматически проявляются, если проект вёлся без учёта Природных Стандартов и природной системности.
Осипов считает одним из городов ближайшего будущего – строительство новой столицы в Сибири и объясняет, с точки зрения принципа равновесия, почему, где и как это неизбежно придётся делать. Ещё один потенциальный образец гармонии — инновационный город будущего, который концептуально проектируется рядом с городом Бангалор, штат Карнатака в Республике Индия.
Интересно, что бизнес без учёта особенностей Природоподобных Технологий, всегда будет более подвержен риску и обречён вечно догонять сбалансированных гармонией коллег. Эта ущербность может касаться концептуальных, организационных и структурных подходов, а также производственного конструктива.
Настоящая рукотворная экология начинается с Природоподобных Технологий. Прятать рукотворные сооружения, созданные без учёта Природных Стандартов за зелёными насаждениями – это псевдоэкология. Заботой А.В. Осипова стали все виды экологии — экология идеологии, политики, государственного устройства, но особенно экология техногенной среды обитания человека, экология дома, города, аграрного сектора. Он объясняет природу и причины ряда новых заболеваний, причину урбанистического (городского техногенного) геноцида и показывает принципы, которые позволяют создавать инженерные объекты с благотворными свойствами, со свойствами урбанистического целительства.

Особое место занимает тема экологии вооружений, экологии оборонного сектора, экологии искусственных космических объектов. Осипов разъясняет причины отсутствия жизнеспособности, или причины малой жизнеспособности у крупных конструкций, например, сверхтяжёлых ракет, подводных крейсеров, авианосцев, а так же у гиперскоростных объектов и объектов, работающих с максимальными перегрузками. Причины проблем он видит в особенностях сборки частей в целое, они разные в каждой ростовой группе и нуждаются в учёте ряда поправочных коэффициентов. Именно из-за этих особенностей в Природе «конструкция» травы, кустов и деревьев такая разная.
Отдельный раздел у А.В. Осипова занимает экология искусственного интеллекта. Алгоритм Природных доминант, исходящий из принципа Триединства, чётко показывает, каким проявлением Золотой Пропорции включается «механизм» абсолютной безопасности для человека от развития искусственного интеллекта.
Рано или поздно, миру потребуется научно-исследовательский Центр Стандартов Природоподобных Технологий, а так же потребуется заключение межгосударственной конвенции о применении Стандартов данных технологий в гуманитарной и техногенной сферах, в том числе IT технологиях, технологиях искусственного интеллекта. Только Природоподобные Технологии, в принципе, могут дать возможность упорядочить и объединить современный мир на здоровой справедливой основе и очень важно исторически, какая страна станет законодательным центром изучения и применения Стандартов Природоподобных Технологий.
Основную часть своих открытий А.В. Осипов отказался патентовать и только попросил последователей ссылаться на автора при использовании его подходов и методик. Он считает проявления Триединства — достоянием всего человечества, а ему лишь удалось увидеть самую малую часть особенностей Природы и рассказать об увиденном феномене.
Пришло время массового применения проявлений Золотой Пропорции, так как его «применяет» сама Природа в своём «конструировании». Технология Природоподобия уже вписана в хронологический ряд прецедентов истории о Золотой Пропорции. Неутомимым исследователям Золотого Сечения история преподнесла очередной подарок, пусть изучают и замеряют новые шедевры различной инженерии и продолжают подтверждать, что они стали таковыми, потому что созданы по золотым канонам – по Природоподобным Технологиям.
Сегодня, благодаря новым открытиям, есть возможность следовать не только Золотой Пропорции, формам золотого прямоугольника и ряду Фибоначчи, а появился главный и ключевой фактор – Стандарты Природных Технологий. Осознанно употребляя эти Стандарты, человечество входит в эру Природоподобных Технологий, что облегчает восприятие рукотворного мира, формирует эстетическое ощущение, открывает тайну силы, жизнестойкости, красоты, гармонии, подсознательного успокоения и удовлетворения.
С уважением Любовь Васильевна Пролубникова и Игорь Иванович Лауткин
Полезные статьи:
— Записаться на семинар Аркадия Осипова;
— Отзывы;
— Что такое Золотое Сечение:
— Что такое Закон Триединства;
— Что такое Природоподобные технологии;
— Заказать индивидуальный проект;
— Курсы для архитектора;
— Все услуги;

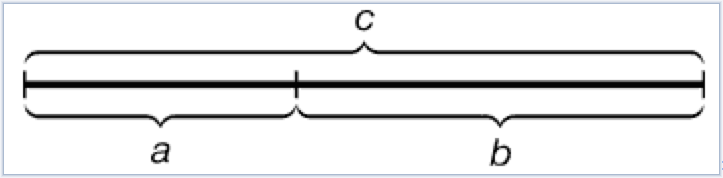
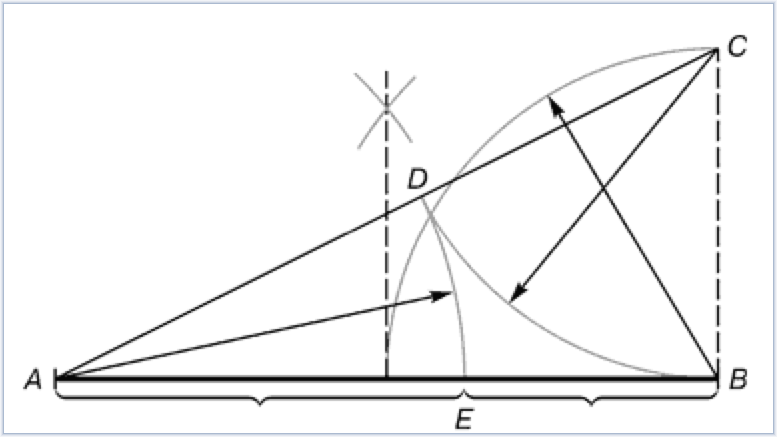
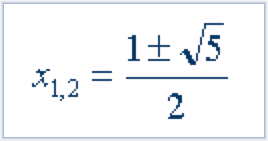
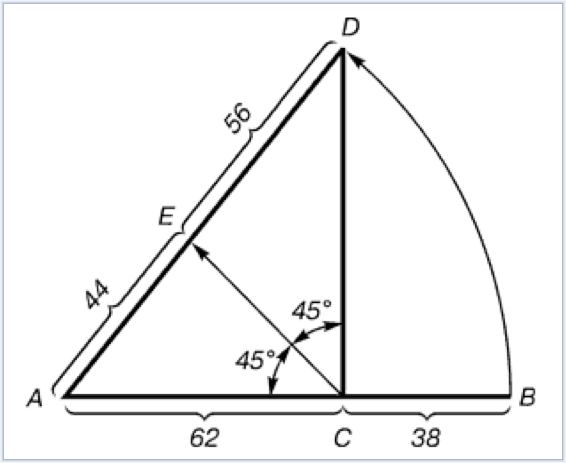
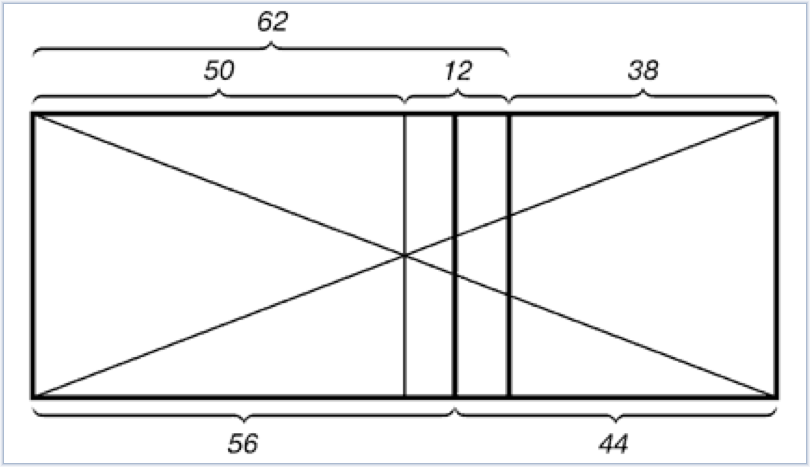
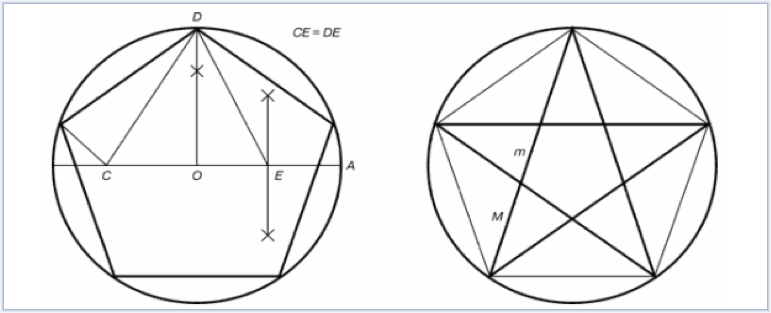
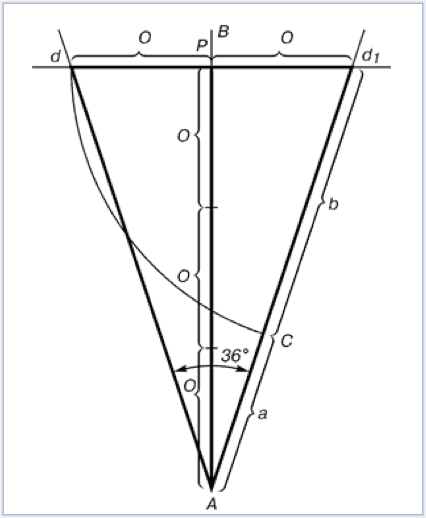




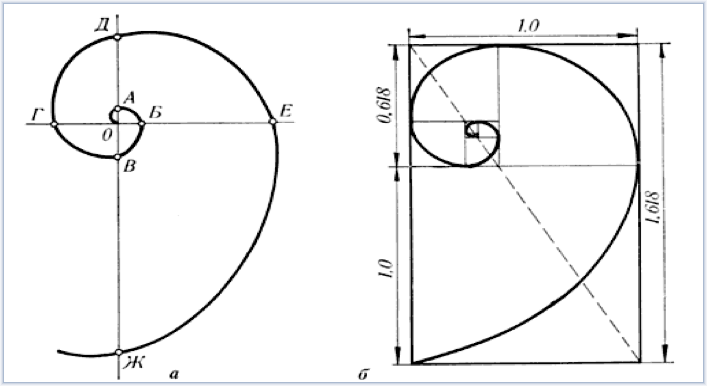




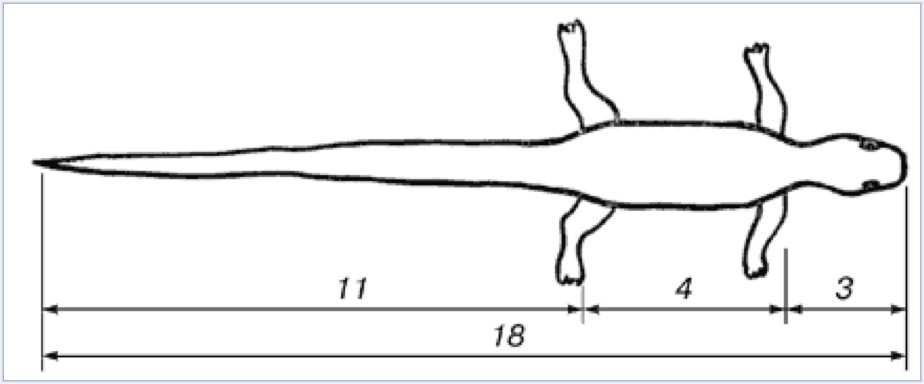
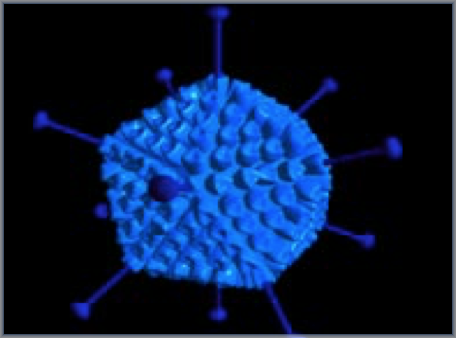

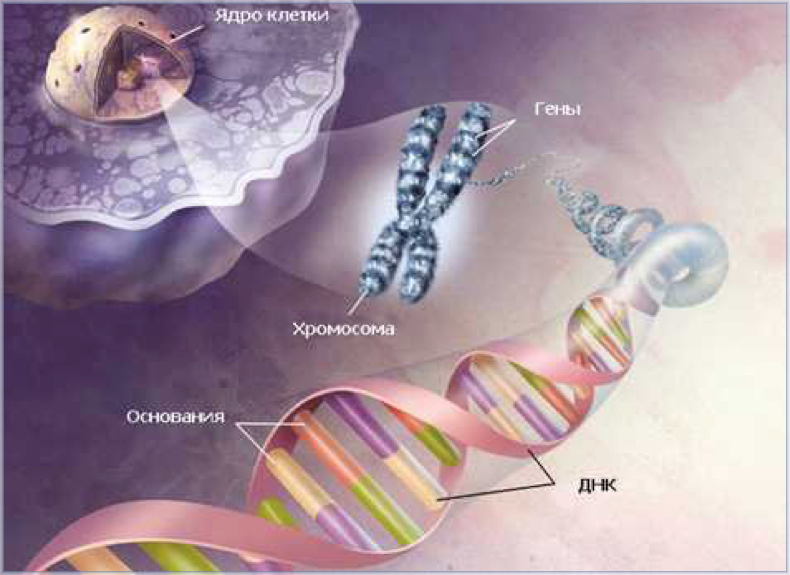





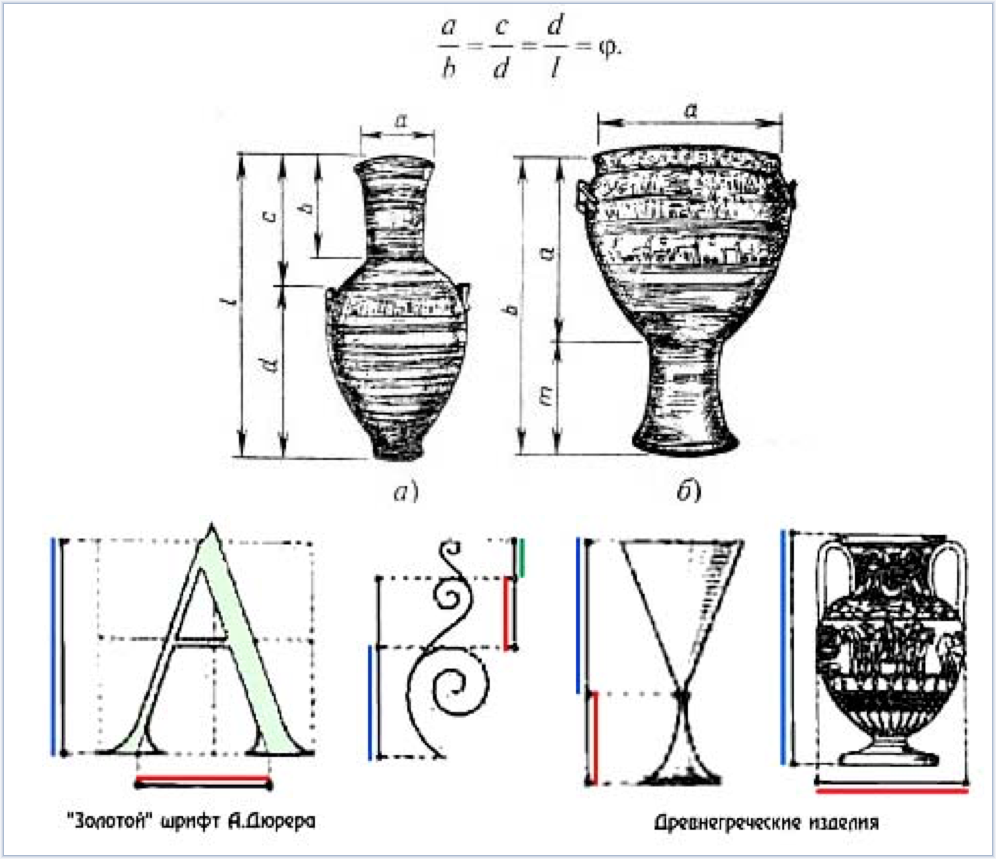






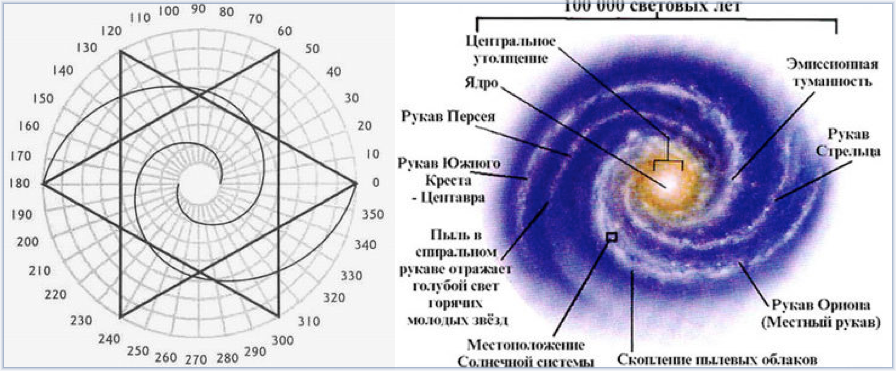













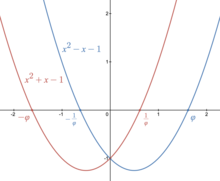





![{displaystyle {begin{aligned}varphi ^{2}&=varphi +1=2.618033dots ,\[5mu]{frac {1}{varphi }}&=varphi -1=0.618033dots .end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff2e5225abf67548cf93c882add3a4b439c4aeb8)

![{displaystyle {begin{aligned}varphi ^{n}&=varphi ^{n-1}+varphi ^{n-3}+cdots +varphi ^{n-1-2m}+varphi ^{n-2-2m}\[5mu]varphi ^{n}-varphi ^{n-1}&=varphi ^{n-2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/048f09b7012c7fbd3d9f32798de6dd5c01acabcd)

![varphi =[1;1,1,1,dots ]=1+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+ddots }}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95682588ffee3530627c3a7b00ff08bbba6e97d4)
![varphi ^{-1}=[0;1,1,1,dots ]=0+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+ddots }}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/165d255e32f4b9af1f9144f15302b147fc3fead2)


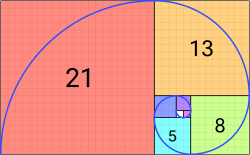
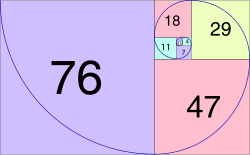








![{displaystyle {begin{aligned}3varphi ^{3}-5varphi ^{2}+4&=3(varphi ^{2}+varphi )-5varphi ^{2}+4\[5mu]&=3[(varphi +1)+varphi ]-5(varphi +1)+4\[5mu]&=varphi +2approx 3.618033.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60ff8508aa117064d60142d447fb0cb58a809848)

![{displaystyle {begin{aligned}varphi ^{0}&=1,\[5mu]varphi ^{1}&=1.618033989...approx 2,\[5mu]varphi ^{2}&=2.618033989...approx 3,\[5mu]varphi ^{3}&=4.236067978...approx 4,\[5mu]varphi ^{4}&=6.854101967...approx 7,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20c9bfd2f9bdc877282b290adc74c88f1dfa63c8)


























![{displaystyle {begin{aligned}{frac {2pi -g}{g}}&={frac {2pi }{2pi -g}}=varphi ,\[8mu]2pi -g&={frac {2pi }{varphi }}approx 222.5^{circ },\[8mu]g&={frac {2pi }{varphi ^{2}}}approx 137.5^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd5f9122b38d09e0cd2992820f27b8587efd167a)





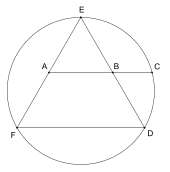
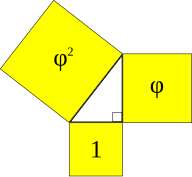
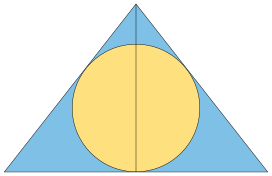
![{displaystyle {begin{aligned}A&={tfrac {s^{2}}{2}}{sqrt {varphi }},\[5mu]theta &=sin ^{-1}{frac {1}{varphi }}approx 38.1727^{circ },\[5mu]theta &=cos ^{-1}{frac {1}{varphi }}approx 51.8273^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f96fa323a2e180a6198f05d33c13e1631854e840)
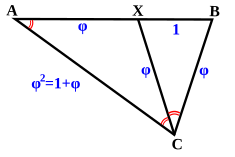
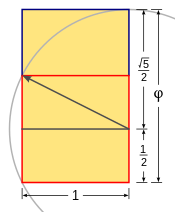
![{displaystyle {begin{aligned}alpha &=2arctan {1 over varphi }approx 63.43495^{circ },\[5mu]beta &=2arctan varphi =pi -arctan 2=arctan 1+arctan 3approx 116.56505^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c5a4321454f4ca1b41b0dbd8f2c6c4afd48467e)
![{displaystyle {begin{aligned}d&={2a over {sqrt {2+varphi }}}=2{sqrt {{3-varphi } over 5}}aapprox 1.05146a,\[5mu]D&=2{sqrt {{2+varphi } over 5}}aapprox 1.70130a.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d00bbc42679ab9e34fdf849ac68de75180cc92c7)
![{displaystyle {begin{aligned}A&=(sin(arctan 2))~a^{2}={2 over {sqrt {5}}}~a^{2}approx 0.89443a^{2},\[5mu]A&={{varphi } over 2}d^{2}approx 0.80902d^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bed70dcf23f16f3f8241aeaf2b56f0897244ff3)

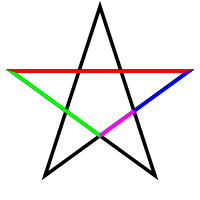

![{displaystyle {begin{aligned}varphi &=1+2sin(pi /10)=1+2sin 18^{circ },\[5mu]varphi &={tfrac {1}{2}}csc(pi /10)={tfrac {1}{2}}csc 18^{circ },\[5mu]varphi &=2cos(pi /5)=2cos 36^{circ },\[5mu]varphi &=2sin(3pi /10)=2sin 54^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c42bbf25d6257a00fad895691aa2c5eb0c6f57a)




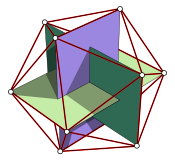

![{displaystyle {begin{aligned}e^{0}+e^{-0}&=2,\[5mu]e^{2pi i/5}+e^{-2pi i/5}&=varphi ^{-1}=-1+varphi ,\[5mu]e^{4pi i/5}+e^{-4pi i/5}&=-varphi .end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bec7bcbd2e99aef0874eb163966c3e2dd9424b86)
![{displaystyle {begin{aligned}e^{pi i}+e^{-pi i}&=-2,\[5mu]e^{pi i/5}+e^{-pi i/5}&=varphi ,\[5mu]e^{3pi i/5}+e^{-3pi i/5}&=-varphi ^{-1}=1-varphi .end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9459634b32b6990a97eb560ce696a3bc2e722513)