Загрузить PDF
Загрузить PDF
Некоторые учащиеся не понимают, как найти площадь круга по исходным данным. Для начала нужно запомнить формулу, по которой вычисляется площадь круга: 
-
1
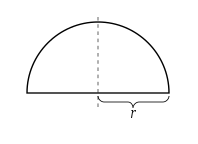
Найдите радиус круга. Радиус – это отрезок, соединяющий центр круга с любой точкой внешней окружности круга. Радиус можно измерить в любом направлении: он будет одним и тем же. Радиус также равен половине диаметра круга. Диаметр – это отрезок, который проходит через центр круга и соединяет две точки внешней окружности круга.[1]
- Как правило, значение радиуса дано в условиях задачи. Довольно трудно найти точный центр круга, если только он не обозначен на круге, который нарисован на бумаге.
- Например, радиус круга равен 6 см.
-
2
Возведите радиус в квадрат. Формула для вычисления площади круга:
, где
– радиус, который возведен во вторую степень (в квадрат).[2]
-
3
Полученный результат умножьте на число Пи. Это число обозначается греческой буквой
и представляет собой математическую константу, которая характеризует взаимосвязь радиуса и площади круга. Число Пи приблизительно равно 3,14. Точное значение числа Пи включает бесконечное количество цифр. Иногда ответ (площадь круга) записывается с постоянной
.[3]
- В нашем примере (r = 6 см) площадь вычисляется так:
-
4
Запишите ответ. Помните, что площадь измеряется в квадратных единицах. Если радиус дан в сантиметрах, площадь измеряется в квадратных сантиметрах. Если радиус дан в миллиметрах, площадь измеряется в квадратных миллиметрах. Уточните у преподавателя, нужно ли представить ответ с постоянной
или в числовой форме, используя приблизительное значение числа Пи. Если требование не ясно, запишите оба варианта ответа.[4]
- В нашем примере (r = 6 см) S = 36
см2 или S = 113,04 см2.
Реклама
- В нашем примере (r = 6 см) S = 36
-
1
Измерьте или запишите диаметр. В некоторых задачах радиус не дан. Вместо радиуса указывается диаметр. Если диаметр нарисован на бумаге, измерьте его с помощью линейки. Скорее всего, числовое значение диаметра будет задано.
- Например, диаметр круга равен 20 мм.
-
2
Разделите диаметр пополам. Помните, что диаметр равен удвоенному радиусу. Поэтому разделите любое значение диаметра на 2, чтобы найти радиус.
- Таким образом, если диаметр круга равен 20 мм, то радиус круга равен 20/2 = 10 мм.
-
3
Воспользуйтесь стандартной формулой для вычисления площади круга. Найдя радиус, воспользуйтесь формулой
, чтобы вычислить площадь круга. Подставьте значение радиуса и выполните вычисления следующим образом:
-
4
Запишите ответ. Помните, что площадь измеряется в квадратных единицах. В нашем примере диаметр дан в миллиметрах, поэтому радиус тоже измеряется в миллиметрах, а площадь в квадратных миллиметрах. В нашем примере S =
мм2.
- Также ответ можно представить в численной форме, используя вместо
приблизительное значение 3,14. В этом случае S = (100)(3,14) = 314 мм2.
Реклама
- Также ответ можно представить в численной форме, используя вместо
-
1
Запишите преобразованную формулу. Если известна длина окружности круга, можно воспользоваться преобразованной формулой для вычисления его площади. Такая формула включает длину окружности, а не радиус, и записывается так:
-
2
Измерьте или запишите длину окружности. В некоторых ситуациях нельзя точно измерить диаметр или радиус. Если диаметр не нарисован или центр не отмечен, очень сложно найти точный центр круга. Длину окружности некоторых предметов (например, сковороды) довольно легко измерить с помощью рулетки, то есть можно найти более точное значение длины окружности, чем диаметра.[5]
- Например, длина окружности круга (или круглого предмета) равна 42 см.
-
3
-
4
Запишите формулу для вычисления площади круга. Запишите преобразованную формулу на основе соотношения между длиной окружности и радиусом. Подставьте последнее равенство в стандартную формулу для вычисления площади круга:[7]
-
5
Воспользуйтесь преобразованной формулой, чтобы решить задачу. Теперь в формуле вместо радиуса присутствует длина окружности, поэтому можно вычислить площадь круга по известной длине окружности. Подставьте значение длины окружности и выполните вычисления следующим образом:[8]
-
6
Запишите ответ. Если длина окружности дана в виде числа, а не произведения числа и
, ответ можно записать с
в знаменателе. Или вместо числа Пи подставьте его приблизительное значение (3,14).[9]
Реклама
-
1
Запишите известные величины. В некоторых задачах дана площадь сектора круга, по которой нужно найти площадь всего круга. Внимательно прочитайте такую задачу; ее условие может выглядеть так: «Площадь сектора круга равна 15
см2. Найдите площадь всего круга».[10]
-
2
Запомните определение сектора. Сектор круга – это часть круга, которая ограничена дугой и двумя радиусами. Пространство между такими радиусами и дугой называется сектором.[11]
-
3
Измерьте центральный угол сектора. Воспользуйтесь транспортиром, чтобы измерить угол между двумя радиусами. Линейку (прямолинейную шкалу) совместите с одним из радиусов, причем центр линейки должен совпадать с центром круга. Затем найдите величину угла; для этого посмотрите на точку пересечения второго радиуса с угломерной шкалой.[12]
- Не перепутайте внутренний и внешний угол между двумя радиусами. В задаче должно быть указано, с каким углом работать. Помните, что сумма внутреннего и внешнего углов равна 360 градусов.
- Во многих задачах центральный угол дан, то есть измерять его не нужно. Например, в задаче может быть сказано: «Центральный угол сектора равен 45 градусов»; если это не так, измерьте центральный угол.
-
4
Используйте преобразованную формулу для вычисления площади круга. Если известны площадь сектора и его центральный угол, используйте следующую преобразованную формулу, чтобы найти площадь круга: [13]
-
-
5
Подставьте известные значения и найдите площадь круга. В нашем примере известно, что центральный угол равен 45 градусов, а площадь сектора равна 15
. Подставьте эти значения в формулу:[14]
-
6
Запишите ответ. В нашем примере сектор составлял одну восьмую полного круга. Поэтому площадь полного круга равна 120
см2. Так как площадь сектора дана с постоянной
, скорее всего, ответ тоже можно представить с этой постоянной.[15]
- Чтобы записать ответ в численной форме, умножьте 120 x 3,14 = 376,8 см2.
Реклама
Об этой статье
Эту страницу просматривали 251 681 раз.
Была ли эта статья полезной?
Формула (формулы) площади круга
Найти площадь круга можно разными способами, в зависимости от известных данных.
По радиусу
Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).
Через диаметр
Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d — диаметр, а π – константа, равная 3,1415…):
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).
Через длину окружности
Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L — длина окружности, а π – константа, равная 3,1415…):
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202 / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).
Какие термины используются для поиска площади круга?
Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:
Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 252 + 252 = 625 + 625 = 1250
- 402 = 1600
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 352 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
S = sr/2
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
S = r2sinα/ 2
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Входит ли окружность (периметр) в площадь круга?
Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.
Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Поделитесь в соцсетях
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
In geometry, the area enclosed by a circle of radius r is πr2. Here the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.
One method of deriving this formula, which originated with Archimedes, involves viewing the circle as the limit of a sequence of regular polygons. The area of a regular polygon is half its perimeter multiplied by the distance from its center to its sides, and the corresponding formula–that the area is half the perimeter times the radius–namely, A = 1/2 × 2πr × r, holds in the limit for a circle.
Although often referred to as the area of a circle in informal contexts, strictly speaking the term disk refers to the interior region of the circle, while circle is reserved for the boundary only, which is a curve and covers no area itself. Therefore, the area of a disk is the more precise phrase for the area enclosed by a circle.
History[edit]
Modern mathematics can obtain the area using the methods of integral calculus or its more sophisticated offspring, real analysis. However, the area of a disk was studied by the Ancient Greeks. Eudoxus of Cnidus in the fifth century B.C. had found that the area of a disk is proportional to its radius squared.[1] Archimedes used the tools of Euclidean geometry to show that the area inside a circle is equal to that of a right triangle whose base has the length of the circle’s circumference and whose height equals the circle’s radius in his book Measurement of a Circle. The circumference is 2πr, and the area of a triangle is half the base times the height, yielding the area π r2 for the disk. Prior to Archimedes, Hippocrates of Chios was the first to show that the area of a disk is proportional to the square of its diameter, as part of his quadrature of the lune of Hippocrates,[2] but did not identify the constant of proportionality.
Historical arguments[edit]
A variety of arguments have been advanced historically to establish the equation 
Using polygons[edit]
The area of a regular polygon is half its perimeter times the apothem. As the number of sides of the regular polygon increases, the polygon tends to a circle, and the apothem tends to the radius. This suggests that the area of a disk is half the circumference of its bounding circle times the radius.[3]
Archimedes’s proof[edit]
Following Archimedes’ argument in The Measurement of a Circle (c. 260 BCE), compare the area enclosed by a circle to a right triangle whose base has the length of the circle’s circumference and whose height equals the circle’s radius. If the area of the circle is not equal to that of the triangle, then it must be either greater or less. We eliminate each of these by contradiction, leaving equality as the only possibility. We use regular polygons in the same way.
Not greater[edit]
Circle with square and octagon inscribed, showing area gap
Suppose that the area C enclosed by the circle is greater than the area T = 1⁄2cr of the triangle. Let E denote the excess amount. Inscribe a square in the circle, so that its four corners lie on the circle. Between the square and the circle are four segments. If the total area of those gaps, G4, is greater than E, split each arc in half. This makes the inscribed square into an inscribed octagon, and produces eight segments with a smaller total gap, G8. Continue splitting until the total gap area, Gn, is less than E. Now the area of the inscribed polygon, Pn = C − Gn, must be greater than that of the triangle.
But this forces a contradiction, as follows. Draw a perpendicular from the center to the midpoint of a side of the polygon; its length, h, is less than the circle radius. Also, let each side of the polygon have length s; then the sum of the sides, ns, is less than the circle circumference. The polygon area consists of n equal triangles with height h and base s, thus equals 1⁄2nhs. But since h < r and ns < c, the polygon area must be less than the triangle area, 1⁄2cr, a contradiction. Therefore, our supposition that C might be greater than T must be wrong.
Not less[edit]
Circle with square and octagon circumscribed, showing area gap
Suppose that the area enclosed by the circle is less than the area T of the triangle. Let D denote the deficit amount. Circumscribe a square, so that the midpoint of each edge lies on the circle. If the total area gap between the square and the circle, G4, is greater than D, slice off the corners with circle tangents to make a circumscribed octagon, and continue slicing until the gap area is less than D. The area of the polygon, Pn, must be less than T.
This, too, forces a contradiction. For, a perpendicular to the midpoint of each polygon side is a radius, of length r. And since the total side length is greater than the circumference, the polygon consists of n identical triangles with total area greater than T. Again we have a contradiction, so our supposition that C might be less than T must be wrong as well.
Therefore, it must be the case that the area enclosed by the circle is precisely the same as the area of the triangle. This concludes the proof.
Rearrangement proof[edit]
Circle area by rearrangement
Following Satō Moshun (Smith & Mikami 1914, pp. 130–132) and Leonardo da Vinci (Beckmann 1976, p. 19), we can use inscribed regular polygons in a different way. Suppose we inscribe a hexagon. Cut the hexagon into six triangles by splitting it from the center. Two opposite triangles both touch two common diameters; slide them along one so the radial edges are adjacent. They now form a parallelogram, with the hexagon sides making two opposite edges, one of which is the base, s. Two radial edges form slanted sides, and the height, h is equal to its apothem (as in the Archimedes proof). In fact, we can also assemble all the triangles into one big parallelogram by putting successive pairs next to each other. The same is true if we increase it to eight sides and so on. For a polygon with 2n sides, the parallelogram will have a base of length ns, and a height h. As the number of sides increases, the length of the parallelogram base approaches half the circle circumference, and its height approaches the circle radius. In the limit, the parallelogram becomes a rectangle with width πr and height r.
-
Unit disk area by rearranging n polygons.
polygon parallelogram n side base height area 4 1.4142136 2.8284271 0.7071068 2.0000000 6 1.0000000 3.0000000 0.8660254 2.5980762 8 0.7653669 3.0614675 0.9238795 2.8284271 10 0.6180340 3.0901699 0.9510565 2.9389263 12 0.5176381 3.1058285 0.9659258 3.0000000 14 0.4450419 3.1152931 0.9749279 3.0371862 16 0.3901806 3.1214452 0.9807853 3.0614675 96 0.0654382 3.1410320 0.9994646 3.1393502 ∞ 1/∞ π 1 π
Modern proofs[edit]
There are various equivalent definitions of the constant π. The conventional definition in pre-calculus geometry is the ratio of the circumference of a circle to its diameter:
However, because the circumference of a circle is not a primitive analytical concept, this definition is not suitable in modern rigorous treatments. A standard modern definition is that π is equal to twice the least positive root of the cosine function or, equivalently, the half-period of the sine (or cosine) function. The cosine function can be defined either as a power series, or as the solution of a certain differential equation. This avoids any reference to circles in the definition of π, so that statements about the relation of π to the circumference and area of circles are actually theorems, rather than definitions, that follow from the analytical definitions of concepts like «area» and «circumference».
The analytical definitions are seen to be equivalent, if it is agreed that the circumference of the circle is measured as a rectifiable curve by means of the integral
The integral appearing on the right is an abelian integral whose value is a half-period of the sine function, equal to π. Thus 
Several of the arguments that follow use only concepts from elementary calculus to reproduce the formula 
Onion proof[edit]
Area of the disk via ring integration
Using calculus, we can sum the area incrementally, partitioning the disk into thin concentric rings like the layers of an onion. This is the method of shell integration in two dimensions. For an infinitesimally thin ring of the «onion» of radius t, the accumulated area is 2πt dt, the circumferential length of the ring times its infinitesimal width (one can approximate this ring by a rectangle with width=2πt and height=dt). This gives an elementary integral for a disk of radius r.
It is rigorously justified by the multivariate substitution rule in polar coordinates. Namely, the area is given by a double integral of the constant function 1 over the disk itself. If D denotes the disk, then the double integral can be computed in polar coordinates as follows:
which is the same result as obtained above.
An equivalent rigorous justification, without relying on the special coordinates of trigonometry, uses the coarea formula. Define a function 









Triangle proof[edit]
Circle unwrapped to form a triangle
The circle and the triangle are equal in area.
Similar to the onion proof outlined above, we could exploit calculus in a different way in order to arrive at the formula for the area of a disk. Consider unwrapping the concentric circles to straight strips. This will form a right angled triangle with r as its height and 2πr (being the outer slice of onion) as its base.
Finding the area of this triangle will give the area of the disk
The opposite and adjacent angles for this triangle are respectively in degrees 9.0430611…, 80.956939… and in radians 0.1578311… OEIS: A233527, 1.4129651…OEIS: A233528.
Explicitly, we imagine dividing up a circle into triangles, each with a height equal to the circle’s radius and a base that is infinitesimally small. The area of each of these triangles is equal to 
It too can be justified by a double integral of the constant function 1 over the disk by reversing the order of integration and using a change of variables in the above iterated integral:
Making the substitution 
which is the same as the above result.
The triangle proof can be reformulated as an application of Green’s theorem in flux-divergence form (i.e. a two-dimensional version of the divergence theorem), in a way that avoids all mention of trigonometry and the constant π. Consider the vector field 
By Green’s theorem, this is the same as the outward flux of r across the circle bounding D:
where n is the unit normal and ds is the arc length measure. For a circle of radius R centered at the origin, we have 

The integral of ds over the whole circle 

Another proof that uses triangles considers the area enclosed by a circle to be made up of an infinite number of triangles (i.e. the triangles each have an angle of d𝜃 at the centre of the circle), each with an area of 1/2 · r2 · d𝜃 (derived from the expression for the area of a triangle: 1/2 · a · b · sin𝜃 = 1/2 · r · r · sin(d𝜃) = 1/2 · r2 · d𝜃). Note that sin(d𝜃) ≈ d𝜃 due to small angle approximation. Through summing the areas of the triangles, the expression for the area of the circle can therefore be found:
Semicircle proof[edit]
Note that the area of a semicircle of radius r can be computed by the integral 
A semicircle of radius r
By trigonometric substitution, we substitute 

The last step follows since the trigonometric identity 


![[0,pi /2]](https://wikimedia.org/api/rest_v1/media/math/render/svg/db58baa407ae179d23402f61cb3edcfd7e4fa5b1)




Therefore, the area of a circle of radius r, which is twice the area of the semi-circle, is equal to 
This particular proof may appear to beg the question, if the sine and cosine functions involved in the trigonometric substitution are regarded as being defined in relation to circles. However, as noted earlier, it is possible to define sine, cosine, and π in a way that is totally independent of trigonometry, in which case the proof is valid by the change of variables formula and Fubini’s theorem, assuming the basic properties of sine and cosine (which can also be proved without assuming anything about their relation to circles).
Isoperimetric inequality[edit]
The circle is the closed curve of least perimeter that encloses the maximum area. This is known as the isoperimetric inequality, which states that if a rectifiable Jordan curve in the Euclidean plane has perimeter C and encloses an area A (by the Jordan curve theorem) then
Moreover, equality holds in this inequality if and only if the curve is a circle, in which case 

Fast approximation[edit]
The calculations Archimedes used to approximate the area numerically were laborious, and he stopped with a polygon of 96 sides. A faster method uses ideas of Willebrord Snell (Cyclometricus, 1621), further developed by Christiaan Huygens (De Circuli Magnitudine Inventa, 1654), described in Gerretsen & Verdenduin (1983, pp. 243–250).
Archimedes’ doubling method[edit]
Given a circle, let un be the perimeter of an inscribed regular n-gon, and let Un be the perimeter of a circumscribed regular n-gon. Then un and Un are lower and upper bounds for the circumference of the circle that become sharper and sharper as n increases, and their average (un + Un)/2 is an especially good approximation to the circumference. To compute un and Un for large n, Archimedes derived the following doubling formulae:
(geometric mean), and
(harmonic mean).
Starting from a hexagon, Archimedes doubled n four times to get a 96-gon, which gave him a good approximation to the circumference of the circle.
In modern notation, we can reproduce his computation (and go further) as follows.
For a unit circle, an inscribed hexagon has u6 = 6, and a circumscribed hexagon has U6 = 4√3.
Doubling seven times yields
-
Archimedes doubling seven times; n = 6×2k.
k n un Un un + Un/4 0 6 6.0000000 6.9282032 3.2320508 1 12 6.2116571 6.4307806 3.1606094 2 24 6.2652572 6.3193199 3.1461443 3 48 6.2787004 6.2921724 3.1427182 4 96 6.2820639 6.2854292 3.1418733 5 192 6.2829049 6.2837461 3.1416628 6 384 6.2831152 6.2833255 3.1416102 7 768 6.2831678 6.2832204 3.1415970
(Here un + Un/2 approximates the circumference of the unit circle, which is 2π, so un + Un/4 approximates π.)
The last entry of the table has 355⁄113 as one of its best rational approximations;
i.e., there is no better approximation among rational numbers with denominator up to 113.
The number 355⁄113 is also an excellent approximation to π, better than any other rational number with denominator less than 16604.[4]
The Snell–Huygens refinement[edit]
Snell proposed (and Huygens proved) a tighter bound than Archimedes’:
This for n = 48 gives a better approximation (about 3.14159292) than Archimedes’ method for n = 768.
Derivation of Archimedes’ doubling formulae[edit]
Circle with similar triangles: circumscribed side, inscribed side and complement, inscribed split side and complement
Let one side of an inscribed regular n-gon have length sn and touch the circle at points A and B. Let A′ be the point opposite A on the circle, so that A′A is a diameter, and A′AB is an inscribed triangle on a diameter. By Thales’ theorem, this is a right triangle with right angle at B. Let the length of A′B be cn, which we call the complement of sn; thus cn2+sn2 = (2r)2. Let C bisect the arc from A to B, and let C′ be the point opposite C on the circle. Thus the length of CA is s2n, the length of C′A is c2n, and C′CA is itself a right triangle on diameter C′C. Because C bisects the arc from A to B, C′C perpendicularly bisects the chord from A to B, say at P. Triangle C′AP is thus a right triangle, and is similar to C′CA since they share the angle at C′. Thus all three corresponding sides are in the same proportion; in particular, we have C′A : C′C = C′P : C′A and AP : C′A = CA : C′C. The center of the circle, O, bisects A′A, so we also have triangle OAP similar to A′AB, with OP half the length of A′B. In terms of side lengths, this gives us
In the first equation C′P is C′O+OP, length r+1⁄2cn, and C′C is the diameter, 2r. For a unit circle we have the famous doubling equation of Ludolph van Ceulen,
If we now circumscribe a regular n-gon, with side A″B″ parallel to AB, then OAB and OA″B″ are similar triangles, with A″B″ : AB = OC : OP. Call the circumscribed side Sn; then this is Sn : sn = 1 : 1⁄2cn. (We have again used that OP is half the length of A′B.) Thus we obtain
Call the inscribed perimeter un = nsn, and the circumscribed perimeter Un = nSn. Then combining equations, we have
so that
This gives a geometric mean equation.
We can also deduce
or
This gives a harmonic mean equation.
Dart approximation[edit]
Unit circle area Monte Carlo integration. Estimate by these 900 samples is 4×
709/900 = 3.15111…
When more efficient methods of finding areas are not available, we can resort to «throwing darts». This Monte Carlo method uses the fact that if random samples are taken uniformly scattered across the surface of a square in which a disk resides, the proportion of samples that hit the disk approximates the ratio of the area of the disk to the area of the square. This should be considered a method of last resort for computing the area of a disk (or any shape), as it requires an enormous number of samples to get useful accuracy; an estimate good to 10−n requires about 100n random samples (Thijssen 2006, p. 273).
Finite rearrangement[edit]
We have seen that by partitioning the disk into an infinite number of pieces we can reassemble the pieces into a rectangle. A remarkable fact discovered relatively recently (Laczkovich 1990) is that we can dissect the disk into a large but finite number of pieces and then reassemble the pieces into a square of equal area. This is called Tarski’s circle-squaring problem. The nature of Laczkovich’s proof is such that it proves the existence of such a partition (in fact, of many such partitions) but does not exhibit any particular partition.
Non-Euclidean circles[edit]
Circles can be defined in non-Euclidean geometry, and in particular in the hyperbolic and elliptic planes.
For example, the unit sphere 
More precisely, fix a point 











We can also measure the area of the spherical disk enclosed within a spherical circle, using the intrinsic surface area measure on the sphere. The area of the disk of radius R is then given by
More generally, if a sphere 

Observe that, as an application of L’Hôpital’s rule, this tends to the Euclidean area 

The hyperbolic case is similar, with the area of a disk of intrinsic radius R in the (constant curvature 
where cosh is the hyperbolic cosine. More generally, for the constant curvature 
These identities are important for comparison inequalities in geometry. For example, the area enclosed by a circle of radius R in a flat space is always greater than the area of a spherical circle and smaller than a hyperbolic circle, provided all three circles have the same (intrinsic) radius. That is,
for all 
In all cases, if 
where equality is achieved precisely for the circle.[5]
Generalizations[edit]
We can stretch a disk to form an ellipse. Because this stretch is a linear transformation of the plane, it has a distortion factor which will change the area but preserve ratios of areas. This observation can be used to compute the area of an arbitrary ellipse from the area of a unit circle.
Consider the unit circle circumscribed by a square of side length 2. The transformation sends the circle to an ellipse by stretching or shrinking the horizontal and vertical diameters to the major and minor axes of the ellipse. The square gets sent to a rectangle circumscribing the ellipse. The ratio of the area of the circle to the square is π/4, which means the ratio of the ellipse to the rectangle is also π/4. Suppose a and b are the lengths of the major and minor axes of the ellipse. Since the area of the rectangle is ab, the area of the ellipse is πab/4.
We can also consider analogous measurements in higher dimensions. For example, we may wish to find the volume inside a sphere. When we have a formula for the surface area, we can use the same kind of «onion» approach we used for the disk.
Bibliography[edit]
- Archimedes (1897), «Measurement of a circle», in Heath, T. L. (ed.), The Works of Archimedes, Cambridge University Press
(Originally published by Cambridge University Press, 1897, based on J. L. Heiberg’s Greek version.) - Beckmann, Petr (1976), A History of Pi, St. Martin’s Griffin, ISBN 978-0-312-38185-1
- Gerretsen, J.; Verdenduin, P. (1983), «Chapter 8: Polygons and Polyhedra», in H. Behnke; F. Bachmann; K. Fladt; H. Kunle (eds.), Fundamentals of Mathematics, Volume II: Geometry, translated by S. H. Gould, MIT Press, pp. 243–250, ISBN 978-0-262-52094-2
(Originally Grundzüge der Mathematik, Vandenhoeck & Ruprecht, Göttingen, 1971.) - Laczkovich, Miklós (1990), «Equidecomposability and discrepancy: A solution to Tarski’s circle squaring problem», Journal für die reine und angewandte Mathematik, 1990 (404): 77–117, doi:10.1515/crll.1990.404.77, MR 1037431, S2CID 117762563
- Lang, Serge (1985), «The length of the circle», Math! : Encounters with High School Students, Springer-Verlag, ISBN 978-0-387-96129-3
- Smith, David Eugene; Mikami, Yoshio (1914), A history of Japanese mathematics, Chicago: Open Court Publishing, pp. 130–132, ISBN 978-0-87548-170-8
- Thijssen, J. M. (2006), Computational Physics, Cambridge University Press, p. 273, ISBN 978-0-521-57588-1
References[edit]
- ^ Stewart, James (2003). Single variable calculus early transcendentals (5th. ed.). Toronto ON: Brook/Cole. pp. 3. ISBN 0-534-39330-6.
However, by indirect reasoning, Eudoxus (fifth century B.C.) used exhaustion to prove the familiar formula for the area of a disk:
- ^ Heath, Thomas L. (2003), A Manual of Greek Mathematics, Courier Dover Publications, pp. 121–132, ISBN 0-486-43231-9.
- ^ Hill, George. Lessons in Geometry: For the Use of Beginners, page 124 (1894).
- ^ Not all best rational approximations are the convergents of the continued fraction!
- ^ Isaac Chavel (2001), Isoperimetric inequalities, Cambridge University Press
External links[edit]
- Science News on Tarski problem Archived 2008-04-13 at the Wayback Machine
In geometry, the area enclosed by a circle of radius r is πr2. Here the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.
One method of deriving this formula, which originated with Archimedes, involves viewing the circle as the limit of a sequence of regular polygons. The area of a regular polygon is half its perimeter multiplied by the distance from its center to its sides, and the corresponding formula–that the area is half the perimeter times the radius–namely, A = 1/2 × 2πr × r, holds in the limit for a circle.
Although often referred to as the area of a circle in informal contexts, strictly speaking the term disk refers to the interior region of the circle, while circle is reserved for the boundary only, which is a curve and covers no area itself. Therefore, the area of a disk is the more precise phrase for the area enclosed by a circle.
History[edit]
Modern mathematics can obtain the area using the methods of integral calculus or its more sophisticated offspring, real analysis. However, the area of a disk was studied by the Ancient Greeks. Eudoxus of Cnidus in the fifth century B.C. had found that the area of a disk is proportional to its radius squared.[1] Archimedes used the tools of Euclidean geometry to show that the area inside a circle is equal to that of a right triangle whose base has the length of the circle’s circumference and whose height equals the circle’s radius in his book Measurement of a Circle. The circumference is 2πr, and the area of a triangle is half the base times the height, yielding the area π r2 for the disk. Prior to Archimedes, Hippocrates of Chios was the first to show that the area of a disk is proportional to the square of its diameter, as part of his quadrature of the lune of Hippocrates,[2] but did not identify the constant of proportionality.
Historical arguments[edit]
A variety of arguments have been advanced historically to establish the equation 
Using polygons[edit]
The area of a regular polygon is half its perimeter times the apothem. As the number of sides of the regular polygon increases, the polygon tends to a circle, and the apothem tends to the radius. This suggests that the area of a disk is half the circumference of its bounding circle times the radius.[3]
Archimedes’s proof[edit]
Following Archimedes’ argument in The Measurement of a Circle (c. 260 BCE), compare the area enclosed by a circle to a right triangle whose base has the length of the circle’s circumference and whose height equals the circle’s radius. If the area of the circle is not equal to that of the triangle, then it must be either greater or less. We eliminate each of these by contradiction, leaving equality as the only possibility. We use regular polygons in the same way.
Not greater[edit]
Circle with square and octagon inscribed, showing area gap
Suppose that the area C enclosed by the circle is greater than the area T = 1⁄2cr of the triangle. Let E denote the excess amount. Inscribe a square in the circle, so that its four corners lie on the circle. Between the square and the circle are four segments. If the total area of those gaps, G4, is greater than E, split each arc in half. This makes the inscribed square into an inscribed octagon, and produces eight segments with a smaller total gap, G8. Continue splitting until the total gap area, Gn, is less than E. Now the area of the inscribed polygon, Pn = C − Gn, must be greater than that of the triangle.
But this forces a contradiction, as follows. Draw a perpendicular from the center to the midpoint of a side of the polygon; its length, h, is less than the circle radius. Also, let each side of the polygon have length s; then the sum of the sides, ns, is less than the circle circumference. The polygon area consists of n equal triangles with height h and base s, thus equals 1⁄2nhs. But since h < r and ns < c, the polygon area must be less than the triangle area, 1⁄2cr, a contradiction. Therefore, our supposition that C might be greater than T must be wrong.
Not less[edit]
Circle with square and octagon circumscribed, showing area gap
Suppose that the area enclosed by the circle is less than the area T of the triangle. Let D denote the deficit amount. Circumscribe a square, so that the midpoint of each edge lies on the circle. If the total area gap between the square and the circle, G4, is greater than D, slice off the corners with circle tangents to make a circumscribed octagon, and continue slicing until the gap area is less than D. The area of the polygon, Pn, must be less than T.
This, too, forces a contradiction. For, a perpendicular to the midpoint of each polygon side is a radius, of length r. And since the total side length is greater than the circumference, the polygon consists of n identical triangles with total area greater than T. Again we have a contradiction, so our supposition that C might be less than T must be wrong as well.
Therefore, it must be the case that the area enclosed by the circle is precisely the same as the area of the triangle. This concludes the proof.
Rearrangement proof[edit]
Circle area by rearrangement
Following Satō Moshun (Smith & Mikami 1914, pp. 130–132) and Leonardo da Vinci (Beckmann 1976, p. 19), we can use inscribed regular polygons in a different way. Suppose we inscribe a hexagon. Cut the hexagon into six triangles by splitting it from the center. Two opposite triangles both touch two common diameters; slide them along one so the radial edges are adjacent. They now form a parallelogram, with the hexagon sides making two opposite edges, one of which is the base, s. Two radial edges form slanted sides, and the height, h is equal to its apothem (as in the Archimedes proof). In fact, we can also assemble all the triangles into one big parallelogram by putting successive pairs next to each other. The same is true if we increase it to eight sides and so on. For a polygon with 2n sides, the parallelogram will have a base of length ns, and a height h. As the number of sides increases, the length of the parallelogram base approaches half the circle circumference, and its height approaches the circle radius. In the limit, the parallelogram becomes a rectangle with width πr and height r.
-
Unit disk area by rearranging n polygons.
polygon parallelogram n side base height area 4 1.4142136 2.8284271 0.7071068 2.0000000 6 1.0000000 3.0000000 0.8660254 2.5980762 8 0.7653669 3.0614675 0.9238795 2.8284271 10 0.6180340 3.0901699 0.9510565 2.9389263 12 0.5176381 3.1058285 0.9659258 3.0000000 14 0.4450419 3.1152931 0.9749279 3.0371862 16 0.3901806 3.1214452 0.9807853 3.0614675 96 0.0654382 3.1410320 0.9994646 3.1393502 ∞ 1/∞ π 1 π
Modern proofs[edit]
There are various equivalent definitions of the constant π. The conventional definition in pre-calculus geometry is the ratio of the circumference of a circle to its diameter:
However, because the circumference of a circle is not a primitive analytical concept, this definition is not suitable in modern rigorous treatments. A standard modern definition is that π is equal to twice the least positive root of the cosine function or, equivalently, the half-period of the sine (or cosine) function. The cosine function can be defined either as a power series, or as the solution of a certain differential equation. This avoids any reference to circles in the definition of π, so that statements about the relation of π to the circumference and area of circles are actually theorems, rather than definitions, that follow from the analytical definitions of concepts like «area» and «circumference».
The analytical definitions are seen to be equivalent, if it is agreed that the circumference of the circle is measured as a rectifiable curve by means of the integral
The integral appearing on the right is an abelian integral whose value is a half-period of the sine function, equal to π. Thus 
Several of the arguments that follow use only concepts from elementary calculus to reproduce the formula 
Onion proof[edit]
Area of the disk via ring integration
Using calculus, we can sum the area incrementally, partitioning the disk into thin concentric rings like the layers of an onion. This is the method of shell integration in two dimensions. For an infinitesimally thin ring of the «onion» of radius t, the accumulated area is 2πt dt, the circumferential length of the ring times its infinitesimal width (one can approximate this ring by a rectangle with width=2πt and height=dt). This gives an elementary integral for a disk of radius r.
It is rigorously justified by the multivariate substitution rule in polar coordinates. Namely, the area is given by a double integral of the constant function 1 over the disk itself. If D denotes the disk, then the double integral can be computed in polar coordinates as follows:
which is the same result as obtained above.
An equivalent rigorous justification, without relying on the special coordinates of trigonometry, uses the coarea formula. Define a function 









Triangle proof[edit]
Circle unwrapped to form a triangle
The circle and the triangle are equal in area.
Similar to the onion proof outlined above, we could exploit calculus in a different way in order to arrive at the formula for the area of a disk. Consider unwrapping the concentric circles to straight strips. This will form a right angled triangle with r as its height and 2πr (being the outer slice of onion) as its base.
Finding the area of this triangle will give the area of the disk
The opposite and adjacent angles for this triangle are respectively in degrees 9.0430611…, 80.956939… and in radians 0.1578311… OEIS: A233527, 1.4129651…OEIS: A233528.
Explicitly, we imagine dividing up a circle into triangles, each with a height equal to the circle’s radius and a base that is infinitesimally small. The area of each of these triangles is equal to 
It too can be justified by a double integral of the constant function 1 over the disk by reversing the order of integration and using a change of variables in the above iterated integral:
Making the substitution 
which is the same as the above result.
The triangle proof can be reformulated as an application of Green’s theorem in flux-divergence form (i.e. a two-dimensional version of the divergence theorem), in a way that avoids all mention of trigonometry and the constant π. Consider the vector field 
By Green’s theorem, this is the same as the outward flux of r across the circle bounding D:
where n is the unit normal and ds is the arc length measure. For a circle of radius R centered at the origin, we have 

The integral of ds over the whole circle 

Another proof that uses triangles considers the area enclosed by a circle to be made up of an infinite number of triangles (i.e. the triangles each have an angle of d𝜃 at the centre of the circle), each with an area of 1/2 · r2 · d𝜃 (derived from the expression for the area of a triangle: 1/2 · a · b · sin𝜃 = 1/2 · r · r · sin(d𝜃) = 1/2 · r2 · d𝜃). Note that sin(d𝜃) ≈ d𝜃 due to small angle approximation. Through summing the areas of the triangles, the expression for the area of the circle can therefore be found:
Semicircle proof[edit]
Note that the area of a semicircle of radius r can be computed by the integral 
A semicircle of radius r
By trigonometric substitution, we substitute 

The last step follows since the trigonometric identity 


![[0,pi /2]](https://wikimedia.org/api/rest_v1/media/math/render/svg/db58baa407ae179d23402f61cb3edcfd7e4fa5b1)




Therefore, the area of a circle of radius r, which is twice the area of the semi-circle, is equal to 
This particular proof may appear to beg the question, if the sine and cosine functions involved in the trigonometric substitution are regarded as being defined in relation to circles. However, as noted earlier, it is possible to define sine, cosine, and π in a way that is totally independent of trigonometry, in which case the proof is valid by the change of variables formula and Fubini’s theorem, assuming the basic properties of sine and cosine (which can also be proved without assuming anything about their relation to circles).
Isoperimetric inequality[edit]
The circle is the closed curve of least perimeter that encloses the maximum area. This is known as the isoperimetric inequality, which states that if a rectifiable Jordan curve in the Euclidean plane has perimeter C and encloses an area A (by the Jordan curve theorem) then
Moreover, equality holds in this inequality if and only if the curve is a circle, in which case 

Fast approximation[edit]
The calculations Archimedes used to approximate the area numerically were laborious, and he stopped with a polygon of 96 sides. A faster method uses ideas of Willebrord Snell (Cyclometricus, 1621), further developed by Christiaan Huygens (De Circuli Magnitudine Inventa, 1654), described in Gerretsen & Verdenduin (1983, pp. 243–250).
Archimedes’ doubling method[edit]
Given a circle, let un be the perimeter of an inscribed regular n-gon, and let Un be the perimeter of a circumscribed regular n-gon. Then un and Un are lower and upper bounds for the circumference of the circle that become sharper and sharper as n increases, and their average (un + Un)/2 is an especially good approximation to the circumference. To compute un and Un for large n, Archimedes derived the following doubling formulae:
(geometric mean), and
(harmonic mean).
Starting from a hexagon, Archimedes doubled n four times to get a 96-gon, which gave him a good approximation to the circumference of the circle.
In modern notation, we can reproduce his computation (and go further) as follows.
For a unit circle, an inscribed hexagon has u6 = 6, and a circumscribed hexagon has U6 = 4√3.
Doubling seven times yields
-
Archimedes doubling seven times; n = 6×2k.
k n un Un un + Un/4 0 6 6.0000000 6.9282032 3.2320508 1 12 6.2116571 6.4307806 3.1606094 2 24 6.2652572 6.3193199 3.1461443 3 48 6.2787004 6.2921724 3.1427182 4 96 6.2820639 6.2854292 3.1418733 5 192 6.2829049 6.2837461 3.1416628 6 384 6.2831152 6.2833255 3.1416102 7 768 6.2831678 6.2832204 3.1415970
(Here un + Un/2 approximates the circumference of the unit circle, which is 2π, so un + Un/4 approximates π.)
The last entry of the table has 355⁄113 as one of its best rational approximations;
i.e., there is no better approximation among rational numbers with denominator up to 113.
The number 355⁄113 is also an excellent approximation to π, better than any other rational number with denominator less than 16604.[4]
The Snell–Huygens refinement[edit]
Snell proposed (and Huygens proved) a tighter bound than Archimedes’:
This for n = 48 gives a better approximation (about 3.14159292) than Archimedes’ method for n = 768.
Derivation of Archimedes’ doubling formulae[edit]
Circle with similar triangles: circumscribed side, inscribed side and complement, inscribed split side and complement
Let one side of an inscribed regular n-gon have length sn and touch the circle at points A and B. Let A′ be the point opposite A on the circle, so that A′A is a diameter, and A′AB is an inscribed triangle on a diameter. By Thales’ theorem, this is a right triangle with right angle at B. Let the length of A′B be cn, which we call the complement of sn; thus cn2+sn2 = (2r)2. Let C bisect the arc from A to B, and let C′ be the point opposite C on the circle. Thus the length of CA is s2n, the length of C′A is c2n, and C′CA is itself a right triangle on diameter C′C. Because C bisects the arc from A to B, C′C perpendicularly bisects the chord from A to B, say at P. Triangle C′AP is thus a right triangle, and is similar to C′CA since they share the angle at C′. Thus all three corresponding sides are in the same proportion; in particular, we have C′A : C′C = C′P : C′A and AP : C′A = CA : C′C. The center of the circle, O, bisects A′A, so we also have triangle OAP similar to A′AB, with OP half the length of A′B. In terms of side lengths, this gives us
In the first equation C′P is C′O+OP, length r+1⁄2cn, and C′C is the diameter, 2r. For a unit circle we have the famous doubling equation of Ludolph van Ceulen,
If we now circumscribe a regular n-gon, with side A″B″ parallel to AB, then OAB and OA″B″ are similar triangles, with A″B″ : AB = OC : OP. Call the circumscribed side Sn; then this is Sn : sn = 1 : 1⁄2cn. (We have again used that OP is half the length of A′B.) Thus we obtain
Call the inscribed perimeter un = nsn, and the circumscribed perimeter Un = nSn. Then combining equations, we have
so that
This gives a geometric mean equation.
We can also deduce
or
This gives a harmonic mean equation.
Dart approximation[edit]
Unit circle area Monte Carlo integration. Estimate by these 900 samples is 4×
709/900 = 3.15111…
When more efficient methods of finding areas are not available, we can resort to «throwing darts». This Monte Carlo method uses the fact that if random samples are taken uniformly scattered across the surface of a square in which a disk resides, the proportion of samples that hit the disk approximates the ratio of the area of the disk to the area of the square. This should be considered a method of last resort for computing the area of a disk (or any shape), as it requires an enormous number of samples to get useful accuracy; an estimate good to 10−n requires about 100n random samples (Thijssen 2006, p. 273).
Finite rearrangement[edit]
We have seen that by partitioning the disk into an infinite number of pieces we can reassemble the pieces into a rectangle. A remarkable fact discovered relatively recently (Laczkovich 1990) is that we can dissect the disk into a large but finite number of pieces and then reassemble the pieces into a square of equal area. This is called Tarski’s circle-squaring problem. The nature of Laczkovich’s proof is such that it proves the existence of such a partition (in fact, of many such partitions) but does not exhibit any particular partition.
Non-Euclidean circles[edit]
Circles can be defined in non-Euclidean geometry, and in particular in the hyperbolic and elliptic planes.
For example, the unit sphere 
More precisely, fix a point 











We can also measure the area of the spherical disk enclosed within a spherical circle, using the intrinsic surface area measure on the sphere. The area of the disk of radius R is then given by
More generally, if a sphere 

Observe that, as an application of L’Hôpital’s rule, this tends to the Euclidean area 

The hyperbolic case is similar, with the area of a disk of intrinsic radius R in the (constant curvature 
where cosh is the hyperbolic cosine. More generally, for the constant curvature 
These identities are important for comparison inequalities in geometry. For example, the area enclosed by a circle of radius R in a flat space is always greater than the area of a spherical circle and smaller than a hyperbolic circle, provided all three circles have the same (intrinsic) radius. That is,
for all 
In all cases, if 
where equality is achieved precisely for the circle.[5]
Generalizations[edit]
We can stretch a disk to form an ellipse. Because this stretch is a linear transformation of the plane, it has a distortion factor which will change the area but preserve ratios of areas. This observation can be used to compute the area of an arbitrary ellipse from the area of a unit circle.
Consider the unit circle circumscribed by a square of side length 2. The transformation sends the circle to an ellipse by stretching or shrinking the horizontal and vertical diameters to the major and minor axes of the ellipse. The square gets sent to a rectangle circumscribing the ellipse. The ratio of the area of the circle to the square is π/4, which means the ratio of the ellipse to the rectangle is also π/4. Suppose a and b are the lengths of the major and minor axes of the ellipse. Since the area of the rectangle is ab, the area of the ellipse is πab/4.
We can also consider analogous measurements in higher dimensions. For example, we may wish to find the volume inside a sphere. When we have a formula for the surface area, we can use the same kind of «onion» approach we used for the disk.
Bibliography[edit]
- Archimedes (1897), «Measurement of a circle», in Heath, T. L. (ed.), The Works of Archimedes, Cambridge University Press
(Originally published by Cambridge University Press, 1897, based on J. L. Heiberg’s Greek version.) - Beckmann, Petr (1976), A History of Pi, St. Martin’s Griffin, ISBN 978-0-312-38185-1
- Gerretsen, J.; Verdenduin, P. (1983), «Chapter 8: Polygons and Polyhedra», in H. Behnke; F. Bachmann; K. Fladt; H. Kunle (eds.), Fundamentals of Mathematics, Volume II: Geometry, translated by S. H. Gould, MIT Press, pp. 243–250, ISBN 978-0-262-52094-2
(Originally Grundzüge der Mathematik, Vandenhoeck & Ruprecht, Göttingen, 1971.) - Laczkovich, Miklós (1990), «Equidecomposability and discrepancy: A solution to Tarski’s circle squaring problem», Journal für die reine und angewandte Mathematik, 1990 (404): 77–117, doi:10.1515/crll.1990.404.77, MR 1037431, S2CID 117762563
- Lang, Serge (1985), «The length of the circle», Math! : Encounters with High School Students, Springer-Verlag, ISBN 978-0-387-96129-3
- Smith, David Eugene; Mikami, Yoshio (1914), A history of Japanese mathematics, Chicago: Open Court Publishing, pp. 130–132, ISBN 978-0-87548-170-8
- Thijssen, J. M. (2006), Computational Physics, Cambridge University Press, p. 273, ISBN 978-0-521-57588-1
References[edit]
- ^ Stewart, James (2003). Single variable calculus early transcendentals (5th. ed.). Toronto ON: Brook/Cole. pp. 3. ISBN 0-534-39330-6.
However, by indirect reasoning, Eudoxus (fifth century B.C.) used exhaustion to prove the familiar formula for the area of a disk:
- ^ Heath, Thomas L. (2003), A Manual of Greek Mathematics, Courier Dover Publications, pp. 121–132, ISBN 0-486-43231-9.
- ^ Hill, George. Lessons in Geometry: For the Use of Beginners, page 124 (1894).
- ^ Not all best rational approximations are the convergents of the continued fraction!
- ^ Isaac Chavel (2001), Isoperimetric inequalities, Cambridge University Press
External links[edit]
- Science News on Tarski problem Archived 2008-04-13 at the Wayback Machine
Нужно найти площадь круга – как можно решить задачу и какие методы для этого использовать? Подробно рассмотрим эту тему и научимся без труда решать типовые задания по математике.
Определения и основные понятия
Перед тем, как приступить к разбору формул и решению задач, нужно запомнить основные определения:
- Круг – плоская геометрическая фигура, представляющая собой скопление точек в пределах окружности.
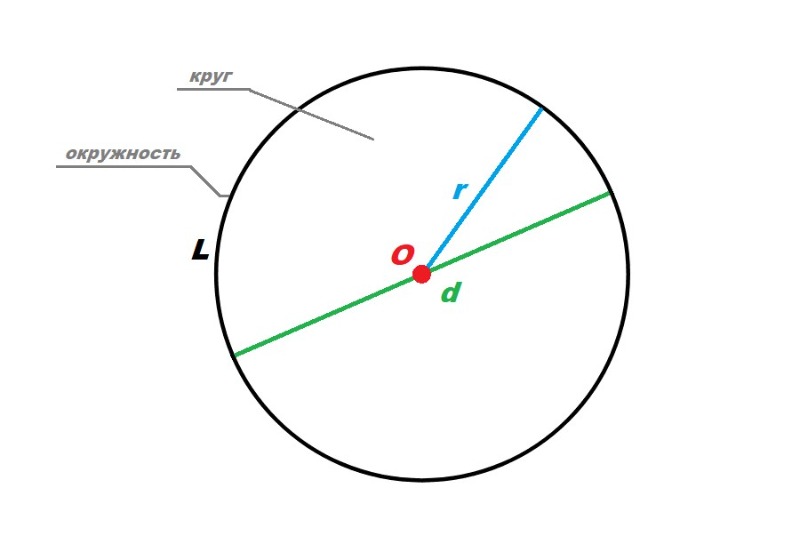
- Окружность – замкнутая линия определенной длины (L), каждая из точек которой равномерно отдалена от центра (О).
- Радиус (r) – расстояние от центра до окружности.
- Диаметр (d) – линия, соединяющая две точки, расположенные на окружности, и пересекающая центр. При этом, d = 2*r.
- π – константа, округленное значение которой равно 3,14.
Площадь круга через диаметр
Для нахождения площади круга можно использовать несколько методов в зависимости от того, о чем говорится в задании. Если мы знаем величину диаметра, то площадь можно найти по формуле S = d²:4*π. То есть диаметр нам нужно возвести в квадрат, а затем разделить получившееся значение на четыре и умножить на 3,14.
Также этим методом можно воспользоваться, если известен радиус. Для этого требуется умножить его на два, в результате чего удастся узнать диаметр. После этого площадь можно будет найти по указанной ранее формуле.
Площадь круга через радиус и длину окружности
Найти площадь такой фигуры, как круг, можно и через радиус, если воспользоваться формулой S = π*r², то есть квадрат радиуса нужно умножить на число Пи. В этом случае диаметр искать не придется, а значит задачу можно будет решить более простым путем.
Еще один способ доступен, если известна длина окружности. Ее требуется возвести в квадрат и разделить на произведение четырех и числа Пи: S = L²:(4*π).
Задачи для тренировки
Теперь, когда основные формулы уже рассмотрены, стоит закрепить свои знания на примере задач из школьной программы. Допустим, нам нужно найти S круга, если известно, что:
- радиус равен 8 дм. В этом случае S = 3.14*8² = 200,96 дм².
- диаметр равен 12 см. Вычисляем S = 12²:4*3,14 = 113,04 см².
- длина окружности равна 16 м. То есть: S = 16²:(4*3,14) = 20,38 м².
Тема, которую мы рассмотрели, не является сложной, особенно если тщательно ее разобрать. Это же касается и других тем по математике – важно своевременно закреплять свои знания, и тогда удастся преуспеть в изучении этого предмета.
Уделять внимание математике нужно с первых лет обучения в школе, ведь именно в начальных классах ребенку прививаются важнейшие базовые знания и навыки. Развитие математических способностей в младшем возрасте создаст надежную основу для дальнейшего обучения.









































![{displaystyle {begin{aligned}mathrm {Area} (r)&{}=int _{0}^{r}2pi t,dt\&{}=2pi left[{frac {t^{2}}{2}}right]_{0}^{r}\&{}=pi r^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22d49256b6928ac3b3624a749b47be687a62092e)
![{displaystyle {begin{aligned}mathrm {Area} (r)&{}=iint _{D}1 d(x,y)\&{}=iint _{D}t dt dtheta \&{}=int _{0}^{r}int _{0}^{2pi }t dtheta dt\&{}=int _{0}^{r}left[ttheta right]_{0}^{2pi }dt\&{}=int _{0}^{r}2pi t,dt\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a18dc84550f7b8aec1a8eabb3d29d23a66147d9e)




![{displaystyle {begin{aligned}mathrm {Area} (r)&{}=int _{0}^{2pi r}{frac {1}{2}}r,du\&{}=left[{frac {1}{2}}ruright]_{0}^{2pi r}\&{}=pi r^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa2816f3bfec2afeff1011d6f763f73f7bbf538f)





![{displaystyle {begin{aligned}mathrm {Area} &{}=int _{0}^{2pi }{frac {1}{2}}r^{2},dtheta \&{}=left[{frac {1}{2}}r^{2}theta right]_{0}^{2pi }\&{}=pi r^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f1ff8135211ae36e2d3087475420d550281b254)