Обновлено: 09.01.2023
2 Процессор компьютера выполняет арифметические и логические операции над двоичными кодами. И поэтому чтобы иметь представление об устройстве компьютера, необходимо познакомиться с основными логическими элементами, лежащими в основе его построения. Для понимания принципа работы таких элементов изучим основные начальные понятия алгебры логики.
4 Первые учения о формах и способах рассуждений возникли в странах Дальнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные древнегреческими мыслителями. Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления от его содержания.
5 Алгебру логики так же называют алгеброй Буля, или булевой алгеброй, по имени английского математика Джорджа Буля, разработавшего в XIX веке ее основные положения.
7 Высказывание (суждение) – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов, их свойствах и отношениях между ними. Высказывание могут принимать только два значения – Истина (обозначается 1) или Ложь (обозначается 0). Высказывания могут быть простыми и составными. Форма мышления
8 Клубника растёт на деревьях. (ложь) или (0) Два умножить на два равно четырём. (истина) или (1) Все мальчики занимаются футболом. (ложь) или (0) Москва – столица России. (истина) или (1) Простые высказывания Форма мышления
10 Сложные высказывания. В саду цветут астры и пионы. Катя любит писать сочинения или решать задачи. Земля движется по круговой или эллиптической орбите. Если на улице дождь, то асфальт мокрый. Голова думает тогда и только тогда, когда язык отдыхает. Форма мышления
14 Все операции алгебры логики определяются таблицами истинности. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Простые высказывания в алгебре логики обозначаются прописными латинскими буквами: A, B, C, D …
15 Операция НЕ- логическое отрицание (инверсия) Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть простое и составное высказывание. Обозначение операции НЕ, Ā, not А, ¬ А. АĀ ложь истина ложь АĀ 01 10
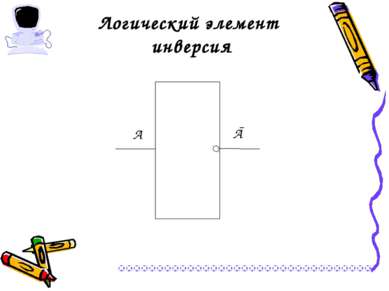
16 Логический элемент инверсия А Ā
17 Операция ИЛИ – логическое сложение (дизъюнкция нестрогая, объединение) Выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и составное высказывание. Обозначения операции: А или В, А or В, А V В. АВАVВАVВ
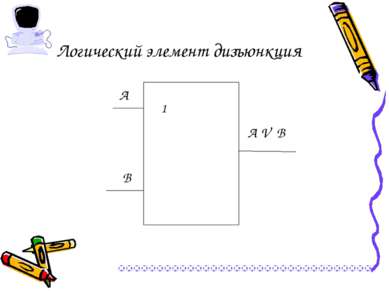
18 Логический элемент дизъюнкция А В А V В 1
19 Операция ИЛИ – логическое сложение (дизъюнкция строгая) Обозначения операции: А xor В, А · В. АВА xor В
20 Операция И – логическое умножение (конъюнкция) Выполняет функцию пересечение двух высказываний (аргументов), в качестве которого может быть и простое, и составное высказывание. Обозначения операции: А и В, А & В, А and В, А Λ В. АВА & В
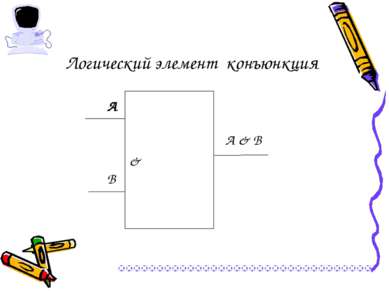
21 Логический элемент конъюнкция & А В А & В
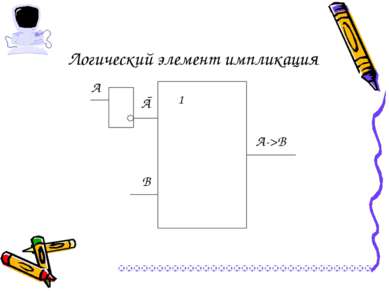
23 Логический элемент импликация А Ā В А->В 1
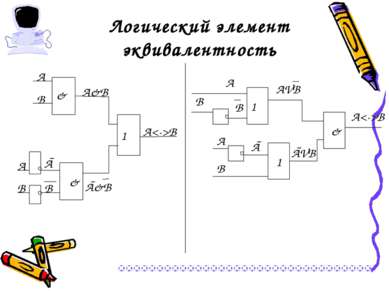
25 Логический элемент эквивалентность А ВА В А 1 & А В & А&ВА&В Ā&В Ā ВВ А ВА В А В В 1 1 АVВАVВ & ĀVВ Ā А В
26 Каждое составное высказывание можно выразить в виде формулы (логического выражения). Логическое выражение(формула) – содержит логические переменные, обозначающие высказывания, соединённые знаками логических операций.
27 Приоритет логических высказываний действия в скобках инверсия конъюнкция дизъюнкция импликация эквивалентность Пример: U (В С) & D Ū Порядок вычисления: 1) Ū 2) (В С) 3) (В С) & D 4) U (В С) & D 5) U В С & D Ū
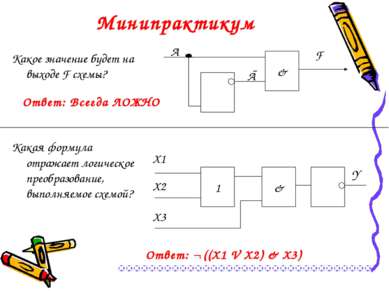
30 Ответ: Всегда ЛОЖНО Минипрактикум Какое значение будет на выходе F схемы? Какая формула отражает логическое преобразование, выполняемое схемой? A & Ā F 1& X1 X2 X3 Y Ответ: ¬ ((X1 V X2) & X3)
32 Составление таблиц истинности по логической формуле Количество строк — 2, где n- это количество логических переменных Количество столбцов — количество логических переменных + количество логических операций. Пример: Ā&В Количество строк = 2 2 = 4 Количество столбцов = = 4 А ВĀА&ВА&В
33 Основные законы булевой алгебры Закон Для дизъюнкции Для конъюнкции 1. АссоциативностьАV(ВVС)=(АVВ)VС= АVВVС А&(В&С)=(А&В)&С= А&В&С 2.КоммутативностьАVВ=ВVАА&В=В&А 3. Дистрибутивность (распределение) АV(В&С)=(АVВ)&(АVС) (АVВ)&(ВVС)=(А&С)VВ (АVВ)&С=(А&С)V(B&C) А&ВVС&В=В&(АVС) 4.ИдемпотентностьАVА=АА&А=А 5. Инволюция Ā=А
34 Закон Для дизъюнкции Для конъюнкции 6. Действие с абсолютно- истинными высказываниями АV1=1А&1=А 7. Действия с абсолютно- ложными высказываниями АV0=АА&0=0 8. Законы де МорганаАVВ=А&ВА&В=АVВ 9. Закон исключенного третьего и закон непротиворечия АVĀ=1А&Ā=0 10.ПоглощенияАV(А&В)=АА&(АVВ)=А 11. Поглощение отрицания АV(Ā&В)=АVВА&(ĀVВ)=А&В Основные законы булевой алгебры
2 Смотреть ответы Добавь ответ +10 баллов
Ответы 2
Другие вопросы по Информатике
Напишите программу на паскале -точка (x, y) находится в области a; – точка (x, y) находится в области b; – точка (x, y) находится в области c; – точка (x, y) находится вне всех обл.
Написать программу поиска чисел , лежащих в интервале от -5 до 5, в последовательности чисел, вводимых с клавиатуры, предшествующих первому ведённому нулю. контрольный пример 1, 10.
Напечатать минимальное число, большее 200, которое нацело делится на 17, напечатать на языке python, , 30 ! .
Каких сведений вам не хватает для ответа на следующие вопросы? запишите все исходные данные,необходимые для решения .1)малыш и карлсон решили по-братски разделить два сладких орешк.
Уисполнителя, который работает с положительными однобайтовыми двоичными числами, две команды, которым присвоены номера: 1. сдвинь влево 2. вычти 1 выполняя первую из них, исполните.
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Логика есть анатомия мышления.
Поспешная логика — значительно хуже глупости.
Она приводит к непоправимым ошибкам.
С помощью логики можно раскрыть
любую тайну и разгадать любой преступный умысел.
Логика — это искусство приходить к непредсказуемому выводу.
Человек, к какой бы исторической цивилизации он ни принадлежал, нуждается в истине . И первобытные люди, и наши современники, познавая окружающий их мир, стремятся получить истину. .
Истина и логика взаимосвязаны, поэтому значение логики нельзя переоценить. Логика помогает доказывать истинные суждения и опровергать ложные, она учит мыслить четко, лаконично, правильно. Логика нужна всем людям, работникам самых различных профессий.
. Это только некоторые из многих преимуществ, которые дает человеку изучение интереснейшей и древнейшей из наук — логики, т. е. науки о законах и формах правильного мышления.
На уроке отражены следующие темы:
— Инверсия, дизъюнкция, конъюнкция, импликация, эквивалентность
— Базовые логические элементы.
Презентация 1сл. ТЕМА УРОКА
Процессор компьютера выполняет арифметические и логические операции над двоичными кодами.
И поэтому, чтобы иметь представление об устройстве компьютера, вспомним основные логическими элементы, лежащими в основе его построения. Для понимания принципа работы таких элементов повторим основные начальные понятия алгебры логики.
Первые учения о формах и способах рассуждений возникли в странах Дальнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные древнегреческими мыслителями. Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления от его содержания.
Детально и глубоко разобрав теорию познания, Аристотель создал труд по логике , который сохраняет своё непреходящее значение и поныне. Здесь он разработал теорию мышления и его формы: понятия , суждения и
Аристотель является и основоположником логики.
Описал двоичную систему счисления с цифрами 0 и 1, на которой основана современная компьютерная техника
В середине XIX века появились первые работы по алгебраизации аристотелевой логики, сформировавшие первооснову исчисления высказываний ( Буль , де Морган , Шрёдер ).
Алгебру логики так же называют
алгеброй Буля, или булевой алгеброй,
по имени английского математика Джорджа Буля, разработавшего в XIX веке ее основные положения.
Джордж Буль по праву считается отцом математической логики. В научных трудах Буля отразилось его убеждение о возможности изучения свойств математических операций, осуществляемых не обязательно над числами. Ученый говорил о символическом методе, который он применял как к изучению дифференцирования и интегрирования, так и к логическому выводу и к теоретико-вероятностным рассуждениям. Именно он построил один из разделов формальной логики в виде некоторой «алгебры», аналогичной алгебре чисел, но не сводящейся к ней. Буль изобрел своеобразную алгебру (впоследствии её назвали булевой) — систему обозначений и правил, применимую к всевозможным объектам, от чисел до предложений. Буль надеялся, что его система, очистив логические аргументы от словесной шелухи, облегчит поиск правильного заключения и сделает его всегда достижимым. Большинство логиков того времени либо игнорировали, либо резко критиковали систему Буля, но ее возможности оказались настолько велики, что она не могла долго оставаться без внимания. Через некоторое время стало понятно, что система Буля хорошо подходит для описания электрических переключателей схем. Это первым из ученых осознал американский логик Чарлз Сандерс Пирс и применил теорию для описания электрических переключательных схем.
Основные формы мышления?
Понятие, высказывание и умозаключение.
Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта.
13 сл. ,14 сл. , 15 сл
Высказывание (суждение) – это форма мышления, в которой
что-либо утверждается или отрицается о свойствах реальных предметов, их свойствах и отношениях между ними.
Высказывание могут принимать только два значения – Истина (обозначается 1) или Ложь (обозначается 0).
Высказывания могут быть простыми и составными.
Простое высказывание состоит из одного высказывания и не содержит логической операции.
Составное высказывание содержит высказывания, объединенные логическими операциями.
Умозаключение — это форма мышления, с помощью которой из одного или нескольких высказываний может быть получено новое высказывание.
В саду цветут астры и пионы.
Катя любит писать сочинения или решать задачи.
Земля движется по круговой или эллиптической орбите.
Если на улице дождь, то асфальт мокрый.
Голова думает тогда и только тогда, когда язык отдыхает.
Все операции алгебры логики определяются таблицами истинности. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний
Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть простое и составное высказывание.
Обозначение операции НЕ, Ā, not А, ¬ А.
21 сл. Логический элемент — ИНВЕРТОР
22 сл. Дизъюнкция
Выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и составное высказывание.
Обозначения операции: А или В, А or В, А V В.
23 сл. Логический элемент ДИЗЪЮНКТОР
24 сл. Конъюнкция
Выполняет функцию пересечение двух высказываний (аргументов), в качестве которого может быть и простое, и составное высказывание.
Обозначения операции: А и В, А & В, А and В, А Λ В.
25 сл. Логический элемент КОНЪЮНКТОР
Практический пример работы Конъюнктора
Практический пример работы Дизюнктора
Практический пример работы Инвертора
Связывает два простых высказывания, из которых первое является условием, а второе – следствием из этого условия.
Обозначения операции: если А, то В; А влечет В; if A then B ; А -> В; А => В
Обозначения операции: А ~ В, А В, А Ξ В
Результат операции эквивалентность истинен тогда и только тогда, когда А и В одновременно истины или ложны.
31 сл. Каждое составное высказывание можно выразить в виде формулы (логического выражения).
Логическое выражение(формула) – содержит логические переменные, обозначающие высказывания, соединённые знаками логических операций.

Задание 1: Напишите следующие высказывания в виде логических выражений.
1. Число 17 нечетное и двузначное.
2. Неверно, что корова – хищное животное.
3. Катя любит писать сочинения или решать задачи.
Задание 2: Постройте отрицание для высказываний:
1. Все ребята умеют плавать.
2. Невозможно создать вечный двигатель.
3. Каждый человек – художник.
Задание 3: Составить таблицы истинности для следующих логических выражений.
Задание 4: Найдите все значения переменных, при которых выражение принимает заданное значение.
Задание 5: Дано сложное логическое выражение: (А˅¬B˅C)˄¬(A˅C)
Сколько логических переменных в данном выражении?
Сколько столбцов будет в таблице истинности, построенной для данного выражения?
Сколько строк будет в таблице истинности, построенной для данного выражения?
Задание 6: Ответьте на вопросы:
1. Что определяет алгебра логики?
2. Какие логические значения могут принимать высказывания?
3. Какие высказывания называются сложными?
4. Что такое конъюнкция?
5. Как обозначается конъюнкция (перечислить все варианты)?
Проверочная работа
Задание 1: Напишите следующие высказывания в виде логических выражений.
1. На уроке физики ученики выполняли лабораторную работу и сообщали результаты исследований учителю.
2. Земля движется по круговой или эллиптической орбите.
3. Неверно, что число 1 есть простоя число.
Задание 2: Постройте отрицание для высказываний:
1. Каждый человек – художник.
2. Человек все может.
Задание 3: Составить таблицы истинности для следующих логических выражений.
Задание 4: Найдите все значения переменных, при которых выражение принимает заданное значение.
Задание 5: Дано сложное логическое выражение: ¬(А˄B)˅(A˄C)
Сколько логических переменных в данном выражении?
Сколько столбцов будет в таблице истинности, построенной для данного выражения?
Сколько строк будет в таблице истинности, построенной для данного выражения?
Процессор компьютера выполняет арифметические и логические операции над двоичными кодами. И поэтому чтобы иметь представление об устройстве компьютера, необходимо познакомиться с основными логическими элементами, лежащими в основе его построения. Для понимания принципа работы таких элементов изучим основные начальные понятия алгебры логики.
Первые учения о формах и способах рассуждений возникли в странах Дальнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные древнегреческими мыслителями. Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления от его содержания.
Алгебру логики так же называют алгеброй Буля, или булевой алгеброй, по имени английского математика Джорджа Буля, разработавшего в XIX веке ее основные положения.
Высказывание (суждение) – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов, их свойствах и отношениях между ними. Высказывание могут принимать только два значения – Истина (обозначается 1) или Ложь (обозначается 0). Высказывания могут быть простыми и составными. Форма мышления
Простые высказывания Форма мышления Клубника растёт на деревьях. (ложь) или (0) Два умножить на два равно четырём. (истина) или (1) Все мальчики занимаются футболом. (ложь) или (0) Москва – столица России. (истина) или (1)
Сложные высказывания. Форма мышления В саду цветут астры и пионы. Катя любит писать сочинения или решать задачи. Земля движется по круговой или эллиптической орбите. Если на улице дождь, то асфальт мокрый. Голова думает тогда и только тогда, когда язык отдыхает.
Все операции алгебры логики определяются таблицами истинности. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Простые высказывания в алгебре логики обозначаются прописными латинскими буквами: A, B, C, D …
Операция НЕ- логическое отрицание (инверсия) Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть простое и составное высказывание. Обозначение операции НЕ, Ā, not А, ¬ А. А Ā ложь истина истина ложь А Ā 0 1 1 0
Логический элемент инверсия
Операция ИЛИ – логическое сложение (дизъюнкция нестрогая, объединение) Выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и составное высказывание. Обозначения операции: А или В, А or В, А V В. А В АVВ 0 0 0 0 1 1 1 0 1 1 1 1
Логический элемент дизъюнкция
Операция ИЛИ – логическое сложение (дизъюнкция строгая) Обозначения операции: А xor В, А · В. А В А xor В 0 0 0 0 1 1 1 0 1 1 1 0
Операция И – логическое умножение (конъюнкция) Выполняет функцию пересечение двух высказываний (аргументов), в качестве которого может быть и простое, и составное высказывание. Обозначения операции: А и В, А & В, А and В, А Λ В. А В А & В 0 0 0 0 1 0 1 0 0 1 1 1
Логический элемент конъюнкция
Логический элемент импликация А
Логический элемент эквивалентность АВ
Каждое составное высказывание можно выразить в виде формулы (логического выражения). Логическое выражение(формула) – содержит логические переменные, обозначающие высказывания, соединённые знаками логических операций.
Приоритет логических высказываний действия в скобках инверсия конъюнкция дизъюнкция импликация эквивалентность Пример: U (В ⇒ С) & D ⇔ Ū Порядок вычисления: 1) Ū 2) (В ⇒ С) 3) (В ⇒ С) & D 4) U (В ⇒ С) & D 5) U В ⇒ С & D ⇔ Ū
Минипрактикум Даны простые высказывания: A= B= C= D= Определите истинность логических выражений: (AVB) (C&D); (A&B) -> (CVD); (AVB) -> (C&D); (A&B) (CVD); (Ā -> B)&(CVD); (C Ā)&B&D; (A&B)VC (A&C)V(A&B); (AVB)VC -> (A&C&D)&(BVD) Проверка
Ответ: Всегда ЛОЖНО Минипрактикум Какое значение будет на выходе F схемы? Какая формула отражает логическое преобразование, выполняемое схемой? Ответ: ¬ ((X1 V X2) & X3)
Составление таблиц истинности по логической формуле Количество строк — 2ⁿ, где n- это количество логических переменных Количество столбцов — количество логических переменных + количество логических операций. Пример: Ā&В Количество строк = 22 = 4 Количество столбцов = 2 + 2 = 4 А В Ā А&В 0 0 1 0 0 1 1 1 1 0 0 0 1 1 0 0
Основные законы булевой алгебры Закон Для дизъюнкции Для конъюнкции 1. Ассоциативность АV(ВVС)=(АVВ)VС= АVВVС А&(В&С)=(А&В)&С= А&В&С 2.Коммутативность АVВ=ВVА А&В=В&А 3.Дистрибутивность (распределение) АV(В&С)=(АVВ)&(АVС) (АVВ)&(ВVС)=(А&С)VВ (АVВ)&С=(А&С)V(B&C) А&ВVС&В=В&(АVС) 4.Идемпотентность АVА=А А&А=А 5.Инволюция Ā=А
Основные законы булевой алгебры Закон Для дизъюнкции Для конъюнкции 6.Действие с абсолютно-истинными высказываниями АV1=1 А&1=А 7.Действия с абсолютно-ложными высказываниями АV0=А А&0=0 8.Законы де Моргана АVВ=А&В А&В=АVВ 9.Закон исключенного третьего и закон непротиворечия АVĀ=1 А&Ā=0 10.Поглощения АV(А&В)=А А&(АVВ)=А 11.Поглощение отрицания АV(Ā&В)=АVВ А&(ĀVВ)=А&В
Формула склеивания (А В) (А В)=А (А В) (А В)=А
Формулы поглощения А (А В)= А А (А В)=А А (Ā В)=А В А (Ā В)=А В
Тестовое задание Начать тест
Презентации этого автора
19.11.2018 скрыт
Читайте также:
- Руссо у сочинение музыки новый подход
- Письмо документ и судьбы и эпохи сочинение егэ
- Сочинение суд над инерцией
- Мой любимый фильм гарри поттер на английском сочинение
- Земляк которым я горжусь сочинение
логики и логические основы построения компьютер а»
Из опыта работы Ермаковой В. В., учителя информатики
МБОУ СОШ № 19 города Белово Кемеровской области
выполняет арифметические и
логические операции над двоичными кодами.
И поэтому чтобы иметь представление об устройстве
компьютера, необходимо познакомиться с основными логическими элементами, лежащими в основе его построения. Для понимания принципа работы таких элементов изучим основные начальные понятия алгебры логики.

Логика — это наука о формах и способах 
мышления.
Термин «логика» происходит от древнегреческого logos, означающего «слово, мысль, понятие, рассуждение, закон»
Основными формами мышления являются понятие, высказывание и умозаключение.

Первые учения о формах и способах рассуждений возникли в странах Дальнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные древнегреческими мыслителями. Основы
формы мышления от его

алгеброй Буля, или булевой алгеброй,
по имени английского математика 

Форма
мышлени
я
Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта.
Понятие имеетНапример,две стородержаниены: понятия
содержание и«персональныйобъём. компьютер – это универсальное электронное устройство для
автоматической обработки информации, предназначенное для одного пользователя.» Объём понятия «персональный компьютер» выражает всю совокупность существующих в настоящее время в мире персональных 

Высказывание (суждение) – это |
мышлени |
|
Форма |
|
|
форма мышления, в которой |
я |
|
что-либо утверждается или |
|
|
отрицается о свойствах |
|
|
реальных предметов, их |
свойствах и отношениях между
Высказываннимие. могут принимать только два значения – Истина (обозначается 1) или Ложь (обозначается 0).
Высказывания могут быть простыми и составными.

Форма
Простые высказывания мышлени
я
Клубника растёт на деревьях.
Два умножить на два равно четырём.
Все мальчики занимаются футболом.
Москва – столица России.



Простое высказывание состоит из одного высказывания и не содержит
логической операции. Составное высказывание содержит
высказывания, объединенные логическими операциями.
Например, высказывание «Процессор является устройством обработки информации и принтер является устройством печати» является составным высказыванием, состоящим


Сложные высказывания

Катя любит писать сочинения или решать задачи.
Земля движется по круговой или эллиптической орбите.
Если на улице дождь, то асфальт мокрый.
Голова думает тогда и только тогда, когда язык отдыхает.
Соседние файлы в папке 13.Презентации
- #
- #
- #
Проверочная работа
Тема: «Основы алгебры логики»
Вариант – 1
Задание 1: Напишите следующие высказывания в виде логических выражений.
1. Число 17 нечетное и двузначное.
2. Неверно, что корова – хищное животное.
3. Катя любит писать сочинения или решать задачи.
Задание 2: Постройте отрицание для высказываний:
1. Все ребята умеют плавать.
2. Невозможно создать вечный двигатель.
3. Каждый человек – художник.
Задание 3: Составить таблицы истинности для следующих логических выражений.
1. ¬(A˄B)˄(A˅B)
2. (A˅¬B)˄С
Задание 4: Найдите все значения переменных, при которых выражение принимает заданное значение.
A˄B˄¬C=1
Задание 5: Дано сложное логическое выражение: (А˅¬B˅C)˄¬(A˅C)
Сколько логических переменных в данном выражении?
Сколько столбцов будет в таблице истинности, построенной для данного выражения?
Сколько строк будет в таблице истинности, построенной для данного выражения?
Задание 6: Ответьте на вопросы:
1. Что определяет алгебра логики?
2. Какие логические значения могут принимать высказывания?
3. Какие высказывания называются сложными?
4. Что такое конъюнкция?
5. Как обозначается конъюнкция (перечислить все варианты)?
Проверочная работа
Тема: «Основы алгебры логики»
Вариант – 2
Задание 1: Напишите следующие высказывания в виде логических выражений.
1. На уроке физики ученики выполняли лабораторную работу и сообщали результаты исследований учителю.
2. Земля движется по круговой или эллиптической орбите.
3. Неверно, что число 1 есть простоя число.
Задание 2: Постройте отрицание для высказываний:
1. Каждый человек – художник.
2. Человек все может.
3. Сегодня в театре идет опера «Евгений Онегин».
Задание 3: Составить таблицы истинности для следующих логических выражений.
1. (¬A˄B)˄(A˅B)
2. ¬(A˄B)˅С
Задание 4: Найдите все значения переменных, при которых выражение принимает заданное значение.
¬(A˅B)˄C =1
Задание 5: Дано сложное логическое выражение: ¬(А˄B)˅(A˄C)
Сколько логических переменных в данном выражении?
Сколько столбцов будет в таблице истинности, построенной для данного выражения?
Сколько строк будет в таблице истинности, построенной для данного выражения?
Задание 6: Ответьте на вопросы:
1. Что такое высказывание?
2. Какие виды высказываний вы знаете?
3. Как обозначаются высказывания?
4. Что такое дизъюнкция?
5. Как обозначается дизъюнкция (перечислить все варианты)?
Урок
По
теме:
«Основы логики. Логические элементы
компьютера»
Логика есть анатомия мышления.
Поспешная логика — значительно хуже глупости.
Она приводит
к непоправимым ошибкам.
С
помощью логики можно раскрыть
любую
тайну и разгадать любой преступный умысел.
Логика — это искусство приходить к
непредсказуемому выводу.
Человек, к какой бы исторической цивилизации он
ни принадлежал, нуждается в истине. И первобытные люди, и наши современники, познавая
окружающий их мир, стремятся получить истину. …
Истина и логика взаимосвязаны, поэтому значение
логики нельзя переоценить. Логика помогает доказывать истинные суждения и
опровергать ложные, она учит мыслить четко, лаконично, правильно. Логика нужна
всем людям, работникам самых различных профессий.
…Это только некоторые из многих преимуществ,
которые дает человеку изучение интереснейшей и древнейшей из наук — логики, т.
е. науки о законах и формах правильного мышления…
На
уроке «Основы логики. Логические элементы компьютера» использованы программы Microsoft PowerPoint,
Microsoft Word,
объектно-ориентированная среда программирования Boland Delphi, Microsoft Excel.
На
уроке отражены следующие темы:
—
Формы мышления
—
Инверсия, дизъюнкция, конъюнкция, импликация, эквивалентность
—
Логические выражения
—
Базовые логические элементы.
Материал
содержит два минипрактикума; тест самопроверки знаний, созданный в объектно-ориентированной
среде программирования Boland Delphi; вопросы и задания по теме «Основы
логики», зачётную работа (14 вариантов).
Ход
урока:
Презентация
1сл. ТЕМА УРОКА
2сл.
Процессор компьютера выполняет арифметические и логические операции над двоичными
кодами.
И поэтому, чтобы иметь представление об устройстве компьютера, вспомним
основные логическими элементы, лежащими в основе его построения. Для понимания
принципа работы таких элементов повторим основные начальные понятия алгебры
логики.
3сл.
ЛОГИКА
— это наука о формах и способах мышления.
Термин «логика» происходит от древнегреческого logos,
означающего «слово, мысль, понятие, рассуждение, закон»
4сл.
Аристотель (сообщение учащихся)
Первые учения о формах и способах рассуждений возникли в странах Дальнего
Востока (Китай, Индия), но в основе современной логики лежат учения, созданные
древнегреческими мыслителями. Основы формальной логики заложил Аристотель,
который впервые отделил логические формы мышления от его содержания.
5сл.
Аристотель
Детально и глубоко разобрав теорию познания, Аристотель создал труд по логике,
который сохраняет своё непреходящее значение и поныне. Здесь он разработал
теорию мышления и
его формы: понятия, суждения и
умозаключения.
Аристотель является и основоположником логики.
6сл.,
7 сл.
Го́тфрид Ви́льгельм Ле́йбниц
(сообщение учащихся)
•
Он заложил основы математической
логики
•
Описал двоичную
систему счисления с цифрами 0 и 1, на которой основана
современная компьютерная
техника
•
Вопрос о создании символической логики
как универсального научного языка рассматривал Лейбниц в 1666
году в работе «Искусство комбинаторики» (De arte combinatoria).
•
В середине XIX века появились первые
работы по алгебраизации аристотелевой логики, сформировавшие первооснову исчисления
высказываний (Буль, де
Морган, Шрёдер).
8 сл. , 9 сл
Джордж Буль (сообщение
учащихся)
Алгебру логики так же
называют
алгеброй Буля, или булевой алгеброй,
по имени английского математика Джорджа Буля, разработавшего в XIX
веке ее основные положения.
•
Джордж Буль по праву считается отцом
математической логики. В научных трудах Буля отразилось его убеждение о
возможности изучения свойств математических операций, осуществляемых не
обязательно над числами. Ученый говорил о символическом методе, который он
применял как к изучению дифференцирования и интегрирования, так и к логическому
выводу и к теоретико-вероятностным рассуждениям. Именно он построил один из
разделов формальной логики в виде некоторой «алгебры», аналогичной
алгебре чисел, но не сводящейся к ней. Буль изобрел своеобразную алгебру
(впоследствии её назвали булевой) — систему обозначений и правил, применимую к
всевозможным объектам, от чисел до предложений. Буль надеялся, что его система,
очистив логические аргументы от словесной шелухи, облегчит поиск правильного
заключения и сделает его всегда достижимым. Большинство логиков того времени
либо игнорировали, либо резко критиковали систему Буля, но ее возможности
оказались настолько велики, что она не могла долго оставаться без внимания.
Через некоторое время стало понятно, что система Буля хорошо подходит для
описания электрических переключателей схем. Это первым из ученых осознал
американский логик Чарлз Сандерс Пирс и применил теорию для описания
электрических переключательных схем.
10
сл.
Основные формы мышления?
11
сл.
Понятие, высказывание и умозаключение.
12
сл.
Понятие – это форма мышления, фиксирующая основные, существенные признаки
объекта.
13
сл. ,14 сл. , 15 сл
Высказывание (суждение) – это форма мышления, в которой
что-либо утверждается или отрицается о свойствах реальных предметов, их
свойствах и отношениях между ними.
Высказывание могут принимать только два значения – Истина (обозначается 1) или
Ложь (обозначается 0).
Высказывания могут быть простыми и составными.
Простое
высказывание состоит из одного высказывания и не содержит логической операции.
Составное высказывание содержит высказывания, объединенные логическими
операциями.
Например,
высказывание
«Процессор является устройством обработки информации и принтер является
устройством печати» является составным высказыванием, состоящим из двух
простых, соединённых союзом «и».
16
сл., 17 сл.
Умозаключение
— это форма мышления, с помощью которой из одного или нескольких высказываний
может быть получено новое высказывание.
Например,
если мы имеем высказывание «Все углы треугольника равны», то мы можем путём умозаключения
доказать, что в этом случае справедливо высказывание «Это треугольник
равносторонний».
18
сл.
Какие высказывания?
|
В |
|
Катя |
|
Земля |
|
Если |
|
Голова |
19
сл.
Все операции алгебры логики определяются таблицами
истинности. Таблица истинности определяет результат выполнения операции для
всех возможных логических значений исходных высказываний
20
сл. ИНВЕРСИЯ
•
Логическая операция НЕ применяется к
одному аргументу, в качестве которого может быть простое и составное высказывание.
•
Обозначение операции НЕ, Ā, not
А, ¬ А.
21
сл. Логический элемент — ИНВЕРТОР
22
сл. Дизъюнкция
•
Выполняет функцию объединения двух
высказываний, в качестве которых может быть и простое, и составное
высказывание.
•
Обозначения операции: А или В, А or
В, А V
В.
23
сл. Логический элемент ДИЗЪЮНКТОР
24
сл. Конъюнкция
•
Выполняет функцию пересечение двух
высказываний (аргументов), в качестве которого может быть и простое, и
составное высказывание.
•
Обозначения операции: А и В, А & В, А and
В, А Λ В.
25
сл. Логический элемент КОНЪЮНКТОР
26
сл.
Практический
пример работы Конъюнктора
27
сл.
Практический
пример работы Дизюнктора
28
сл.
Практический пример работы Инвертора
29
сл.
Операция «ЕСЛИ – ТО» — логическое следование (импликация)
•
Связывает два простых высказывания, из
которых первое является условием, а второе – следствием из этого условия.
Обозначения
операции: если А, то В; А влечет В; if A then B;
А -> В; А => В
30
сл.
Операция «А тогда и только тогда, когда В»
(эквивалентность, равнозначность)
•
Обозначения операции: А ~ В, А <=>
В, А Ξ В
•
Результат операции эквивалентность истинен
тогда и только тогда, когда А и В одновременно истины или ложны.
31
сл. Каждое составное высказывание можно выразить в виде формулы (логического
выражения).
Логическое
выражение(формула) – содержит логические переменные, обозначающие
высказывания, соединённые знаками логических операций.
32
сл.
Приоритет
логических высказываний
•
действия в скобках
•
инверсия
•
конъюнкция
•
дизъюнкция
•
импликация
•
эквивалентность
•
Пример:
U Ú
(В ⇒
С) & D ⇔
Ū
Порядок вычисления:
1) Ū
2) (В ⇒
С)
3) (В
⇒
С) & D
4) U Ú
(В ⇒
С) & D
5) U Ú
В ⇒
С & D ⇔
Ū
33
сл.
Минипрактикум
Даны
простые высказывания:
A={Процессор
– устройство для обработки информации}
B={Сканер
– устройство вывода информации}
C={Монитор
– устройство ввода информации}
D={Клавиатура
– устройство вывода информации}
•
Определите истинность логических
выражений:
1.(AVB)
<=> (C&D);
2.(A&B)
-> (CVD);
3.(AVB)
-> (C&D);
4.(A&B)
<=> (CVD);
1.(Ā
-> B)&(CVD);
2.(C
<=> Ā)&B&D;
3.(A&B)VC
<=> (A&C)V(A&B);
4.(AVB)VC
-> (A&C&D)&(BVD)
34
сл.
Правильные
ответы
Часть
ребят выполняют ТЕСТ (два вида) за компьютером, а другая часть — работает
совместно с учителем.
35
сл.
36
сл.
37
сл.
38 сл., 39 сл.
Постройте
логические схемы, соответствующие логическим выражениям и найдите значения
логических выражений:

Сл.
40, 41
Сл
42
ПРАКТИЧЕСКАЯ РАБОТА
Создание в электронных таблицах Microsoft Excel
таблиц истинности. Определить в скольких случаях загорится лампочка?
«В скольких случаях загорится лампочка?»
Сл.
43-46
Основные
законы Булевой алгебры
Литература
Ø Угринович,
Н. Д. Информатика и ИКТ. Профильный уровень. Учебник 10-11 классов/Н. Д.
Угинович. – М.: БИНОМ. Лаборатория знаний, 2008.
Ø Макарова,
Н. В. Информатика и ИКТ. Учебник 8-9 класс/Под ред. Проф. Н. В. Макаровой. –
СПб.: Питер, 2007.
Ø http://ru.wikipedia.org/wiki/%C1%F3%EB%FC,_%C4%E6%EE%F0%E4%E6
Ø http://ru.wikipedia.org/wiki/%C0%F0%E8%F1%F2%EE%F2%E5%EB%FC
Ø http://yandex.ru/yandsearch?text=%D0%BB%D0%BE%D0%B3%D0%B8%D0%BA%D0%B0+%D0%B8+%D0%BA%D0%BE%D0%BC%D0%BF%D1%8C%D1%8E%D1%82%D0%B5%D1%80+%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8&lr=64
1
«Основы логики и логические основы построения компьютера»
2
Процессор компьютера выполняет арифметические и логические операции над двоичными кодами. И поэтому чтобы иметь представление об устройстве компьютера, необходимо познакомиться с основными логическими элементами, лежащими в основе его построения. Для понимания принципа работы таких элементов изучим основные начальные понятия алгебры логики.
3
Логика — это наука о формах и способах мышления. Термин «логика» происходит от древнегреческого logos, означающего «слово, мысль, понятие, рассуждение, закон» Основными формами мышления являются понятие, высказывание и умозаключение.
4
Первые учения о формах и способах рассуждений возникли в странах Дальнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные древнегреческими мыслителями. Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления от его содержания.
5
Алгебру логики так же называют алгеброй Буля, или булевой алгеброй, по имени английского математика Джорджа Буля, разработавшего в XIX веке ее основные положения.
6
Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта. Понятие имеет две стороны: содержание и объём. Например, содержание понятия «персональный компьютер – это универсальное электронное устройство для автоматической обработки информации, предназначенное для одного пользователя.» Объём понятия «персональный компьютер» выражает всю совокупность существующих в настоящее время в мире персональных компьютеров. Форма мышления
7
Высказывание (суждение) – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов, их свойствах и отношениях между ними. Высказывание могут принимать только два значения – Истина (обозначается 1) или Ложь (обозначается 0). Высказывания могут быть простыми и составными. Форма мышления
8
Клубника растёт на деревьях. (ложь) или (0) Два умножить на два равно четырём. (истина) или (1) Все мальчики занимаются футболом. (ложь) или (0) Москва – столица России. (истина) или (1) Простые высказывания Форма мышления
9
Простое высказывание состоит из одного высказывания и не содержит логической операции. Составное высказывание содержит высказывания, объединенные логическими операциями. Например, высказывание «Процессор является устройством обработки информации и принтер является устройством печати» является составным высказыванием, состоящим из двух простых, соединённых союзом «и».
10
Сложные высказывания. В саду цветут астры и пионы. Катя любит писать сочинения или решать задачи. Земля движется по круговой или эллиптической орбите. Если на улице дождь, то асфальт мокрый. Голова думает тогда и только тогда, когда язык отдыхает. Форма мышления
11
Предикаты Высказывание состоит из понятий, и его можно сравнить с арифметическим выражением. В математической логике рассматриваются предикаты, т. е. функциональные зависимости от неопределённых понятий (терминов), которые можно сравнить с переменными в уравнении. В предикатах 1 порядка один из терминов является неопределённым понятием: «X – человек». В предикатах 2 порядка два термина неопределённы: «X любит Y». В предикатах 3 порядка неопределённы три термина: «Z – сын X и Y». Преобразуем в высказывания: «Сократ – человек»; «Ксантиппа любит Сократа»; «Софрониск – сын Сократа и Ксантиппы»
12
Умозаключение — это форма мышления, с помощью которой из одного или нескольких высказываний может быть получено новое высказывание. Форма мышления Например, если мы имеем высказывание «Все углы треугольника равны», то мы можем путём умозаключения доказать, что в этом случае справедливо высказывание «Это треугольник равносторонний».
13
В качестве основных логических операций в составных высказываниях используются: НЕ ( логическое отрицание, инверсия) ИЛИ (логическое сложение, дизъюнкция) И (логическое умножение, конъюнкция) Операция «ЕСЛИ — ТО» (логическое следование, импликация) Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность)
14
Все операции алгебры логики определяются таблицами истинности. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Простые высказывания в алгебре логики обозначаются прописными латинскими буквами: A, B, C, D …
15
Операция НЕ- логическое отрицание (инверсия) Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть простое и составное высказывание. Обозначение операции НЕ, Ā, not А, ¬ А. АĀ ложь истина ложь АĀ 01 10
16
Логический элемент инверсия А Ā
17
Операция ИЛИ – логическое сложение (дизъюнкция нестрогая, объединение) Выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и составное высказывание. Обозначения операции: А или В, А or В, А V В. АВАVВАVВ
18
Логический элемент дизъюнкция А В А V В 1
19
Операция ИЛИ – логическое сложение (дизъюнкция строгая) Обозначения операции: А xor В, А · В. АВА xor В
20
Операция И – логическое умножение (конъюнкция) Выполняет функцию пересечение двух высказываний (аргументов), в качестве которого может быть и простое, и составное высказывание. Обозначения операции: А и В, А & В, А and В, А Λ В. АВА & В
21
Логический элемент конъюнкция & А В А & В
22
Операция «ЕСЛИ – ТО» — логическое следование (импликация) Связывает два простых высказывания, из которых первое является условием, а второе – следствием из этого условия. Обозначения операции: если А, то В; А влечет В; if A then B; А -> В; А => В АВЕсли А, то В
23
Логический элемент импликация А Ā В А->В 1
24
Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность) Обозначения операции: А ~ В, А В, А Ξ В Результат операции эквивалентность истинен тогда и только тогда, когда А и В одновременно истины или ложны. АВА ~ В
25
Логический элемент эквивалентность А<->ВА<->В А 1 & А В & А&ВА&В Ā&В Ā ВВ А<->ВА<->В А В В 1 1 АVВАVВ & ĀVВ Ā А В
26
Каждое составное высказывание можно выразить в виде формулы (логического выражения). Логическое выражение(формула) – содержит логические переменные, обозначающие высказывания, соединённые знаками логических операций.
27
Приоритет логических высказываний действия в скобках инверсия конъюнкция дизъюнкция импликация эквивалентность Пример: U (В С) & D Ū Порядок вычисления: 1) Ū 2) (В С) 3) (В С) & D 4) U (В С) & D 5) U В С & D Ū
28
Минипрактикум Даны простые высказывания : A={Процессор – устройство для обработки информации} B={Сканер – устройство вывода информации} C={Монитор – устройство ввода информации} D={Клавиатура – устройство вывода информации} Определите истинность логических выражений: (AVB) (C&D); (A&B) -> (CVD); (AVB) -> (C&D); (A&B) (CVD); (Ā -> B)&(CVD); (C Ā)&B&D; (A&B)VC (A&C)V(A&B); (AVB)VC -> (A&C&D)&(BVD) Проверка
29
Правильные ответы (AVB) (C&D) = 0 (A&B) -> (CVD) = 1 (AVB) -> (C&D) = 0 (A&B) (CVD) = 1 (Ā -> B)&(CVD) = 0 (C Ā)&B&D = 0 (A&B)VC (A&C)V(A&B) = 1 (AVB)VC -> (A&C&D)&(BVD) = 0 A=1 B=0 C=0 D=0 Назад
30
Ответ: Всегда ЛОЖНО Минипрактикум Какое значение будет на выходе F схемы? Какая формула отражает логическое преобразование, выполняемое схемой? A & Ā F 1& X1 X2 X3 Y Ответ: ¬ ((X1 V X2) & X3)
31
Практическая работа ПК Создание в электронных таблицах Microsoft Excel(OpenOffice.org Calc) таблиц истинности логических функций: -Конъюнкции -Дизъюнкции -Инверсии -Импликации -Эквивалентности
32
Составление таблиц истинности по логической формуле Количество строк — 2, где n- это количество логических переменных Количество столбцов — количество логических переменных + количество логических операций. Пример: Ā&В Количество строк = 2 2 = 4 Количество столбцов = = 4 А ВĀА&ВА&В
33
Основные законы булевой алгебры Закон Для дизъюнкции Для конъюнкции 1. АссоциативностьАV(ВVС)=(АVВ)VС= АVВVС А&(В&С)=(А&В)&С= А&В&С 2.КоммутативностьАVВ=ВVАА&В=В&А 3. Дистрибутивность (распределение) АV(В&С)=(АVВ)&(АVС) (АVВ)&(ВVС)=(А&С)VВ (АVВ)&С=(А&С)V(B&C) А&ВVС&В=В&(АVС) 4.ИдемпотентностьАVА=АА&А=А 5. Инволюция Ā=А
34
Закон Для дизъюнкции Для конъюнкции 6. Действие с абсолютно- истинными высказываниями АV1=1А&1=А 7. Действия с абсолютно- ложными высказываниями АV0=АА&0=0 8. Законы де МорганаАVВ=А&ВА&В=АVВ 9. Закон исключенного третьего и закон непротиворечия АVĀ=1А&Ā=0 10.ПоглощенияАV(А&В)=АА&(АVВ)=А 11. Поглощение отрицания АV(Ā&В)=АVВА&(ĀVВ)=А&В Основные законы булевой алгебры
35
Формула склеивания (А В) (А В)=А
36
Формулы поглощения А (А В)= А А (Ā В)=А В
Урок
По теме:
«Основы логики. Логические элементы компьютера»
Логика есть анатомия мышления.
Поспешная логика — значительно хуже глупости.
Она приводит к непоправимым ошибкам.
С помощью логики можно раскрыть
любую тайну и разгадать любой преступный умысел.
Логика — это искусство приходить к непредсказуемому выводу.
Человек, к какой бы исторической цивилизации он ни принадлежал, нуждается в истине. И первобытные люди, и наши современники, познавая окружающий их мир, стремятся получить истину. …
Истина и логика взаимосвязаны, поэтому значение логики нельзя переоценить. Логика помогает доказывать истинные суждения и опровергать ложные, она учит мыслить четко, лаконично, правильно. Логика нужна всем людям, работникам самых различных профессий.
…Это только некоторые из многих преимуществ, которые дает человеку изучение интереснейшей и древнейшей из наук — логики, т. е. науки о законах и формах правильного мышления…
На уроке «Основы логики. Логические элементы компьютера» использованы программы Microsoft PowerPoint, Microsoft Word, объектно-ориентированная среда программирования Boland Delphi, Microsoft Excel.
На уроке отражены следующие темы:
— Формы мышления
— Инверсия, дизъюнкция, конъюнкция, импликация, эквивалентность
— Логические выражения
— Базовые логические элементы.
Материал содержит два минипрактикума; тест самопроверки знаний, созданный в объектно-ориентированной среде программирования Boland Delphi; вопросы и задания по теме «Основы логики», зачётную работа (14 вариантов).
Ход урока:
Презентация 1сл. ТЕМА УРОКА
2сл.
Процессор компьютера выполняет арифметические и логические операции над двоичными кодами.
И поэтому, чтобы иметь представление об устройстве компьютера, вспомним основные логическими элементы, лежащими в основе его построения. Для понимания принципа работы таких элементов повторим основные начальные понятия алгебры логики.
3сл.
ЛОГИКА — это наука о формах и способах мышления.
Термин «логика» происходит от древнегреческого logos, означающего «слово, мысль, понятие, рассуждение, закон»
4сл.
Аристотель (сообщение учащихся)
Первые учения о формах и способах рассуждений возникли в странах Дальнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные древнегреческими мыслителями. Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления от его содержания.
5сл.
Аристотель
Детально и глубоко разобрав теорию познания, Аристотель создал труд по логике, который сохраняет своё непреходящее значение и поныне. Здесь он разработал теорию мышления и его формы: понятия, суждения и
умозаключения.
Аристотель является и основоположником логики.
6сл., 7 сл.
Го́тфрид Ви́льгельм Ле́йбниц (сообщение учащихся)
- Он заложил основы математической логики
- Описал двоичную систему счисления с цифрами 0 и 1, на которой основана современная компьютерная техника
- Вопрос о создании символической логики как универсального научного языка рассматривал Лейбниц в 1666 году в работе «Искусство комбинаторики» (De arte combinatoria).
- В середине XIX века появились первые работы по алгебраизации аристотелевой логики, сформировавшие первооснову исчисления высказываний (Буль, де Морган, Шрёдер).
8 сл. , 9 сл
Джордж Буль (сообщение учащихся)
Алгебру логики так же называют
алгеброй Буля, или булевой алгеброй,
по имени английского математика Джорджа Буля, разработавшего в XIX веке ее основные положения.
- Джордж Буль по праву считается отцом математической логики. В научных трудах Буля отразилось его убеждение о возможности изучения свойств математических операций, осуществляемых не обязательно над числами. Ученый говорил о символическом методе, который он применял как к изучению дифференцирования и интегрирования, так и к логическому выводу и к теоретико-вероятностным рассуждениям. Именно он построил один из разделов формальной логики в виде некоторой «алгебры», аналогичной алгебре чисел, но не сводящейся к ней. Буль изобрел своеобразную алгебру (впоследствии её назвали булевой) — систему обозначений и правил, применимую к всевозможным объектам, от чисел до предложений. Буль надеялся, что его система, очистив логические аргументы от словесной шелухи, облегчит поиск правильного заключения и сделает его всегда достижимым. Большинство логиков того времени либо игнорировали, либо резко критиковали систему Буля, но ее возможности оказались настолько велики, что она не могла долго оставаться без внимания. Через некоторое время стало понятно, что система Буля хорошо подходит для описания электрических переключателей схем. Это первым из ученых осознал американский логик Чарлз Сандерс Пирс и применил теорию для описания электрических переключательных схем.
10 сл.
Основные формы мышления?
11 сл.
Понятие, высказывание и умозаключение.
12 сл.
Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта.
13 сл. ,14 сл. , 15 сл
Высказывание (суждение) – это форма мышления, в которой
что-либо утверждается или отрицается о свойствах реальных предметов, их свойствах и отношениях между ними.
Высказывание могут принимать только два значения – Истина (обозначается 1) или Ложь (обозначается 0).
Высказывания могут быть простыми и составными.
Простое высказывание состоит из одного высказывания и не содержит логической операции.
Составное высказывание содержит высказывания, объединенные логическими операциями.
Например,
высказывание «Процессор является устройством обработки информации и принтер является устройством печати» является составным высказыванием, состоящим из двух простых, соединённых союзом «и».
16 сл., 17 сл.
Умозаключение — это форма мышления, с помощью которой из одного или нескольких высказываний может быть получено новое высказывание.
Например, если мы имеем высказывание «Все углы треугольника равны», то мы можем путём
умозаключения
доказать, что в этом случае справедливо высказывание «Это треугольник равносторонний».
18 сл.
Какие высказывания?
| В саду цветут астры и пионы. |
| Катя любит писать сочинения или решать задачи. |
| Земля движется по круговой или эллиптической орбите. |
| Если на улице дождь, то асфальт мокрый. |
| Голова думает тогда и только тогда, когда язык отдыхает. |
19 сл.
Все операции алгебры логики определяются таблицами истинности. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний
20 сл. ИНВЕРСИЯ
- Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть простое и составное высказывание.
- Обозначение операции НЕ, Ā, not А, ¬ А.
21 сл. Логический элемент — ИНВЕРТОР
22 сл. Дизъюнкция
- Выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и составное высказывание.
- Обозначения операции: А или В, А or В, А V В.
23 сл. Логический элемент ДИЗЪЮНКТОР
24 сл. Конъюнкция
- Выполняет функцию пересечение двух высказываний (аргументов), в качестве которого может быть и простое, и составное высказывание.
- Обозначения операции: А и В, А & В, А and В, А Λ В.
25 сл. Логический элемент КОНЪЮНКТОР
26 сл.
Практический пример работы Конъюнктора
27 сл.
Практический пример работы Дизюнктора
28 сл.
Практический пример работы Инвертора
29 сл.
Операция «ЕСЛИ – ТО» — логическое следование (импликация)
- Связывает два простых высказывания, из которых первое является условием, а второе – следствием из этого условия.
Обозначения операции: если А, то В; А влечет В; if A then B; А -> В; А => В
30 сл.
Операция «А тогда и только тогда, когда В»
(эквивалентность, равнозначность)
- Обозначения операции: А ~ В, А <=> В, А Ξ В
- Результат операции эквивалентность истинен тогда и только тогда, когда А и В одновременно истины или ложны.
31 сл. Каждое составное высказывание можно выразить в виде формулы (логического выражения).
Логическое выражение(формула) – содержит логические переменные, обозначающие высказывания, соединённые знаками логических операций.
32 сл.
Приоритет логических высказываний
- действия в скобках
- инверсия
- конъюнкция
- дизъюнкция
- импликация
- эквивалентность
- Пример:
U Ú (В ⇒ С) & D ⇔ Ū
Порядок вычисления:
1) Ū
2) (В ⇒ С)
3) (В ⇒ С) & D
4) U Ú (В ⇒ С) & D
5) U Ú В ⇒ С & D ⇔ Ū
33 сл.
Минипрактикум
Даны простые высказывания:
A={Процессор – устройство для обработки информации}
B={Сканер – устройство вывода информации}
C={Монитор – устройство ввода информации}
D={Клавиатура – устройство вывода информации}
- Определите истинность логических выражений:
1.(AVB) <=> (C&D);
2.(A&B) -> (CVD);
3.(AVB) -> (C&D);
4.(A&B) <=> (CVD);
1.(Ā -> B)&(CVD);
2.(C <=> Ā)&B&D;
3.(A&B)VC <=> (A&C)V(A&B);
4.(AVB)VC -> (A&C&D)&(BVD)
34 сл.
Правильные ответы
Часть ребят выполняют ТЕСТ (два вида) за компьютером, а другая часть — работает совместно с учителем.
35 сл.
36 сл.
37 сл.
38 сл., 39 сл.
Постройте логические схемы, соответствующие логическим выражениям и найдите значения логических выражений:
Сл. 40, 41
Сл 42
ПРАКТИЧЕСКАЯ РАБОТА
Создание в электронных таблицах Microsoft Excel таблиц истинности. Определить в скольких случаях загорится лампочка?
«В скольких случаях загорится лампочка?»
Сл. 43-46
Основные законы Булевой алгебры
Литература
- Угринович, Н. Д. Информатика и ИКТ. Профильный уровень. Учебник 10-11 классов/Н. Д. Угинович. – М.: БИНОМ. Лаборатория знаний, 2008.
- Макарова, Н. В. Информатика и ИКТ. Учебник 8-9 класс/Под ред. Проф. Н. В. Макаровой. – СПб.: Питер, 2007.
- http://ru.wikipedia.org/wiki/%C1%F3%EB%FC,_%C4%E6%EE%F0%E4%E6
- http://ru.wikipedia.org/wiki/%C0%F0%E8%F1%F2%EE%F2%E5%EB%FC
- http://yandex.ru/yandsearch?text=%D0%BB%D0%BE%D0%B3%D0%B8%D0%BA%D0%B0+%D0%B8+%D0%BA%D0%BE%D0%BC%D0%BF%D1%8C%D1%8E%D1%82%D0%B5%D1%80+%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8&lr=64