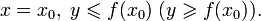В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.
Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).
Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.
Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.
Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:
- окружность с центральной точкой А;
- прямая а — касательная к ней;
- радиус АВ, проведенный к касательной.
Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.
Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.
В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.
Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Задача
У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.
Решение:
Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.
Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.
∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°
Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно,
АВ = 62°.
Ответ:
АВ = 62°.
Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.
Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.
Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.
Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.
Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.
Задача 1
У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.
Решение
Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.
∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).
Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:
∠BDC = ∠BDA × 2 = 30° × 2 = 60°
Итак, угол между касательными составляет 60°.
Ответ: ∠BDA = 60°.
Задача 2
К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.
Решение
Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.
Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.
∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°
Ответ: ∠NМК = 65°.
Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.
Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.
Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.
AB2 = AD × AC
Задача 1
Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.
Решение
Исходя из соотношения касательной и секущей МА 2 = МВ × МС.
Найдем длину внешней части секущей:
МС = МВ — ВС = 16 — 12 = 4 (см)
МА2 = МВ × МС = 16 х 4 = 64
МА = √
64= 8 (см)
Ответ: MA = 8 см.
Задача 2
Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.
Решение
Допустим, что МО = у, а радиус окружности обозначим как R.
В таком случае МВ = у + R, а МС = у – R.
Поскольку МВ = 2 МА, значит:
МА = МВ : 2 = (у + R) : 2
Согласно теореме о касательной и секущей, МА2 = МВ × МС.
Значит:
(у + R)2 : 4 = (у + R) × (у — R)
Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:
(у + R) : 4 = (у — R)
у = 5R : 3
Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).
Ответ: MO = 10 см.
Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.
Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.
Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.
Согласно свойствам угла между касательной и хордой, ∠АВС = ½
АВ.
Ответ:
АВ = 64°.
У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.
Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.
Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:
Ответ: ∠ОМК = 6°.
Tangent to a curve. The red line is tangential to the curve at the point marked by a red dot.
Tangent plane to a sphere
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that «just touches» the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve.[1] More precisely, a straight line is said to be a tangent of a curve y = f(x) at a point x = c if the line passes through the point (c, f(c)) on the curve and has slope f‘(c), where f‘ is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.
As it passes through the point where the tangent line and the curve meet, called the point of tangency, the tangent line is «going in the same direction» as the curve, and is thus the best straight-line approximation to the curve at that point.
The tangent line to a point on a differentiable curve can also be thought of as a tangent line approximation, the graph of the affine function that best approximates the original function at the given point.[2]
Similarly, the tangent plane to a surface at a given point is the plane that «just touches» the surface at that point. The concept of a tangent is one of the most fundamental notions in differential geometry and has been extensively generalized; see Tangent space.
The word «tangent» comes from the Latin tangere, «to touch».
History[edit]
Euclid makes several references to the tangent (ἐφαπτομένη ephaptoménē) to a circle in book III of the Elements (c. 300 BC).[3] In Apollonius’ work Conics (c. 225 BC) he defines a tangent as being a line such that no other straight line could
fall between it and the curve.[4]
Archimedes (c. 287 – c. 212 BC) found the tangent to an Archimedean spiral by considering the path of a point moving along the curve.[4]
In the 1630s Fermat developed the technique of adequality to calculate tangents and other problems in analysis and used this to calculate tangents to the parabola. The technique of adequality is similar to taking the difference between 


These methods led to the development of differential calculus in the 17th century. Many people contributed. Roberval discovered a general method of drawing tangents, by considering a curve as described by a moving point whose motion is the resultant of several simpler motions.[6]
René-François de Sluse and Johannes Hudde found algebraic algorithms for finding tangents.[7] Further developments included those of John Wallis and Isaac Barrow, leading to the theory of Isaac Newton and Gottfried Leibniz.
An 1828 definition of a tangent was «a right line which touches a curve, but which when produced, does not cut it».[8] This old definition prevents inflection points from having any tangent. It has been dismissed and the modern definitions are equivalent to those of Leibniz, who defined the tangent line as the line through a pair of infinitely close points on the curve.
Tangent line to a plane curve[edit]
The intuitive notion that a tangent line «touches» a curve can be made more explicit by considering the sequence of straight lines (secant lines) passing through two points, A and B, those that lie on the function curve. The tangent at A is the limit when point B approximates or tends to A. The existence and uniqueness of the tangent line depends on a certain type of mathematical smoothness, known as «differentiability.» For example, if two circular arcs meet at a sharp point (a vertex) then there is no uniquely defined tangent at the vertex because the limit of the progression of secant lines depends on the direction in which «point B» approaches the vertex.
At most points, the tangent touches the curve without crossing it (though it may, when continued, cross the curve at other places away from the point of tangent). A point where the tangent (at this point) crosses the curve is called an inflection point. Circles, parabolas, hyperbolas and ellipses do not have any inflection point, but more complicated curves do have, like the graph of a cubic function, which has exactly one inflection point, or a sinusoid, which has two inflection points per each period of the sine.
Conversely, it may happen that the curve lies entirely on one side of a straight line passing through a point on it, and yet this straight line is not a tangent line. This is the case, for example, for a line passing through the vertex of a triangle and not intersecting it otherwise—where the tangent line does not exist for the reasons explained above. In convex geometry, such lines are called supporting lines.
At each point, the moving line is always tangent to the curve. Its slope is the derivative; green marks positive derivative, red marks negative derivative and black marks zero derivative. The point (x,y) = (0,1) where the tangent intersects the curve, is not a max, or a min, but is a point of inflection.
Analytical approach[edit]
The geometrical idea of the tangent line as the limit of secant lines serves as the motivation for analytical methods that are used to find tangent lines explicitly. The question of finding the tangent line to a graph, or the tangent line problem, was one of the central questions leading to the development of calculus in the 17th century. In the second book of his Geometry, René Descartes[9] said of the problem of constructing the tangent to a curve, «And I dare say that this is not only the most useful and most general problem in geometry that I know, but even that I have ever desired to know».[10]
Intuitive description[edit]
Suppose that a curve is given as the graph of a function, y = f(x). To find the tangent line at the point p = (a, f(a)), consider another nearby point q = (a + h, f(a + h)) on the curve. The slope of the secant line passing through p and q is equal to the difference quotient
As the point q approaches p, which corresponds to making h smaller and smaller, the difference quotient should approach a certain limiting value k, which is the slope of the tangent line at the point p. If k is known, the equation of the tangent line can be found in the point-slope form:
More rigorous description[edit]
To make the preceding reasoning rigorous, one has to explain what is meant by the difference quotient approaching a certain limiting value k. The precise mathematical formulation was given by Cauchy in the 19th century and is based on the notion of limit. Suppose that the graph does not have a break or a sharp edge at p and it is neither plumb nor too wiggly near p. Then there is a unique value of k such that, as h approaches 0, the difference quotient gets closer and closer to k, and the distance between them becomes negligible compared with the size of h, if h is small enough. This leads to the definition of the slope of the tangent line to the graph as the limit of the difference quotients for the function f. This limit is the derivative of the function f at x = a, denoted f ′(a). Using derivatives, the equation of the tangent line can be stated as follows:
Calculus provides rules for computing the derivatives of functions that are given by formulas, such as the power function, trigonometric functions, exponential function, logarithm, and their various combinations. Thus, equations of the tangents to graphs of all these functions, as well as many others, can be found by the methods of calculus.
How the method can fail[edit]
Calculus also demonstrates that there are functions and points on their graphs for which the limit determining the slope of the tangent line does not exist. For these points the function f is non-differentiable. There are two possible reasons for the method of finding the tangents based on the limits and derivatives to fail: either the geometric tangent exists, but it is a vertical line, which cannot be given in the point-slope form since it does not have a slope, or the graph exhibits one of three behaviors that precludes a geometric tangent.
The graph y = x1/3 illustrates the first possibility: here the difference quotient at a = 0 is equal to h1/3/h = h−2/3, which becomes very large as h approaches 0. This curve has a tangent line at the origin that is vertical.
The graph y = x2/3 illustrates another possibility: this graph has a cusp at the origin. This means that, when h approaches 0, the difference quotient at a = 0 approaches plus or minus infinity depending on the sign of x. Thus both branches of the curve are near to the half vertical line for which y=0, but none is near to the negative part of this line. Basically, there is no tangent at the origin in this case, but in some context one may consider this line as a tangent, and even, in algebraic geometry, as a double tangent.
The graph y = |x| of the absolute value function consists of two straight lines with different slopes joined at the origin. As a point q approaches the origin from the right, the secant line always has slope 1. As a point q approaches the origin from the left, the secant line always has slope −1. Therefore, there is no unique tangent to the graph at the origin. Having two different (but finite) slopes is called a corner.
Finally, since differentiability implies continuity, the contrapositive states discontinuity implies non-differentiability. Any such jump or point discontinuity will have no tangent line. This includes cases where one slope approaches positive infinity while the other approaches negative infinity, leading to an infinite jump discontinuity
Equations[edit]
When the curve is given by y = f(x) then the slope of the tangent is
so by the point–slope formula the equation of the tangent line at (X, Y) is
where (x, y) are the coordinates of any point on the tangent line, and where the derivative is evaluated at 
When the curve is given by y = f(x), the tangent line’s equation can also be found[12] by using polynomial division to divide 


When the equation of the curve is given in the form f(x, y) = 0 then the value of the slope can be found by implicit differentiation, giving
The equation of the tangent line at a point (X,Y) such that f(X,Y) = 0 is then[11]
This equation remains true if 


For algebraic curves, computations may be simplified somewhat by converting to homogeneous coordinates. Specifically, let the homogeneous equation of the curve be g(x, y, z) = 0 where g is a homogeneous function of degree n. Then, if (X, Y, Z) lies on the curve, Euler’s theorem implies
It follows that the homogeneous equation of the tangent line is
The equation of the tangent line in Cartesian coordinates can be found by setting z=1 in this equation.[13]
To apply this to algebraic curves, write f(x, y) as
where each ur is the sum of all terms of degree r. The homogeneous equation of the curve is then
Applying the equation above and setting z=1 produces
as the equation of the tangent line.[14] The equation in this form is often simpler to use in practice since no further simplification is needed after it is applied.[13]
If the curve is given parametrically by
then the slope of the tangent is
giving the equation for the tangent line at 
If 
Normal line to a curve[edit]
The line perpendicular to the tangent line to a curve at the point of tangency is called the normal line to the curve at that point. The slopes of perpendicular lines have product −1, so if the equation of the curve is y = f(x) then slope of the normal line is
and it follows that the equation of the normal line at (X, Y) is
Similarly, if the equation of the curve has the form f(x, y) = 0 then the equation of the normal line is given by[16]
If the curve is given parametrically by
then the equation of the normal line is[15]
Angle between curves[edit]
The angle between two curves at a point where they intersect is defined as the angle between their tangent lines at that point. More specifically, two curves are said to be tangent at a point if they have the same tangent at a point, and orthogonal if their tangent lines are orthogonal.[17]
Multiple tangents at a point[edit]
The limaçon trisectrix: a curve with two tangents at the origin.
The formulas above fail when the point is a singular point. In this case there may be two or more branches of the curve that pass through the point, each branch having its own tangent line. When the point is the origin, the equations of these lines can be found for algebraic curves by factoring the equation formed by eliminating all but the lowest degree terms from the original equation. Since any point can be made the origin by a change of variables (or by translating the curve) this gives a method for finding the tangent lines at any singular point.
For example, the equation of the limaçon trisectrix shown to the right is
Expanding this and eliminating all but terms of degree 2 gives
which, when factored, becomes
So these are the equations of the two tangent lines through the origin.[18]
When the curve is not self-crossing, the tangent at a reference point may still not be uniquely defined because the curve is not differentiable at that point although it is differentiable elsewhere. In this case the left and right derivatives are defined as the limits of the derivative as the point at which it is evaluated approaches the reference point from respectively the left (lower values) or the right (higher values). For example, the curve y = |x | is not differentiable at x = 0: its left and right derivatives have respective slopes −1 and 1; the tangents at that point with those slopes are called the left and right tangents.[19]
Sometimes the slopes of the left and right tangent lines are equal, so the tangent lines coincide. This is true, for example, for the curve y = x 2/3, for which both the left and right derivatives at x = 0 are infinite; both the left and right tangent lines have equation x = 0.
Tangent line to a space curve[edit]
Tangent circles[edit]
Two pairs of tangent circles. Above internally and below externally tangent
Two circles of non-equal radius, both in the same plane, are said to be tangent to each other if they meet at only one point. Equivalently, two circles, with radii of ri and centers at (xi, yi), for i = 1, 2 are said to be tangent to each other if
- Two circles are externally tangent if the distance between their centres is equal to the sum of their radii.
- Two circles are internally tangent if the distance between their centres is equal to the difference between their radii.[20]
Tangent plane to a surface[edit]
«Tangent plane» redirects here. For the geographical concept, see Local tangent plane.
|
This section needs expansion. You can help by adding to it. (May 2022) |
The tangent plane to a surface at a given point p is defined in an analogous way to the tangent line in the case of curves. It is the best approximation of the surface by a plane at p, and can be obtained as the limiting position of the planes passing through 3 distinct points on the surface close to p as these points converge to p.
Higher-dimensional manifolds[edit]
More generally, there is a k-dimensional tangent space at each point of a k-dimensional manifold in the n-dimensional Euclidean space.
See also[edit]
- Newton’s method
- Normal (geometry)
- Osculating circle
- Osculating curve
- Perpendicular
- Subtangent
- Supporting line
- Tangent cone
- Tangential angle
- Tangential component
- Tangent lines to circles
- Tangent vector
- Multiplicity (mathematics)#Behavior of a polynomial function near a multiple root
- Algebraic curve#Tangent at a point
References[edit]
- ^ Leibniz, G., «Nova Methodus pro Maximis et Minimis», Acta Eruditorum, Oct. 1684.
- ^ Dan Sloughter (2000) . «Best Affine Approximations»
- ^ Euclid. «Euclid’s Elements». Retrieved 1 June 2015.
- ^ a b Shenk, Al. «e-CALCULUS Section 2.8» (PDF). p. 2.8. Retrieved 1 June 2015.
- ^ Katz, Victor J. (2008). A History of Mathematics (3rd ed.). Addison Wesley. p. 510. ISBN 978-0321387004.
- ^ Wolfson, Paul R. (2001). «The Crooked Made Straight: Roberval and Newton on Tangents». The American Mathematical Monthly. 108 (3): 206–216. doi:10.2307/2695381. JSTOR 2695381.
- ^ Katz, Victor J. (2008). A History of Mathematics (3rd ed.). Addison Wesley. pp. 512–514. ISBN 978-0321387004.
- ^ Noah Webster, American Dictionary of the English Language (New York: S. Converse, 1828), vol. 2, p. 733, [1]
- ^ Descartes, René (1954). The geometry of René Descartes. Courier Dover. p. 95. ISBN 0-486-60068-8.
- ^ R. E. Langer (October 1937). «Rene Descartes». American Mathematical Monthly. Mathematical Association of America. 44 (8): 495–512. doi:10.2307/2301226. JSTOR 2301226.
- ^ a b Edwards Art. 191
- ^ Strickland-Constable, Charles, «A simple method for finding tangents to polynomial graphs», Mathematical Gazette, November 2005, 466–467.
- ^ a b Edwards Art. 192
- ^ Edwards Art. 193
- ^ a b Edwards Art. 196
- ^ Edwards Art. 194
- ^ Edwards Art. 195
- ^ Edwards Art. 197
- ^ Thomas, George B. Jr., and Finney, Ross L. (1979), Calculus and Analytic Geometry, Addison Wesley Publ. Co.: p. 140.
- ^ «Circles For Leaving Certificate Honours Mathematics by Thomas O’Sullivan 1997».
Sources[edit]
- J. Edwards (1892). Differential Calculus. London: MacMillan and Co. pp. 143 ff.
External links[edit]
Wikimedia Commons has media related to Tangency.
- «Tangent line», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. «Tangent Line». MathWorld.
- Tangent to a circle With interactive animation
- Tangent and first derivative — An interactive simulation
Tangent to a curve. The red line is tangential to the curve at the point marked by a red dot.
Tangent plane to a sphere
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that «just touches» the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve.[1] More precisely, a straight line is said to be a tangent of a curve y = f(x) at a point x = c if the line passes through the point (c, f(c)) on the curve and has slope f‘(c), where f‘ is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.
As it passes through the point where the tangent line and the curve meet, called the point of tangency, the tangent line is «going in the same direction» as the curve, and is thus the best straight-line approximation to the curve at that point.
The tangent line to a point on a differentiable curve can also be thought of as a tangent line approximation, the graph of the affine function that best approximates the original function at the given point.[2]
Similarly, the tangent plane to a surface at a given point is the plane that «just touches» the surface at that point. The concept of a tangent is one of the most fundamental notions in differential geometry and has been extensively generalized; see Tangent space.
The word «tangent» comes from the Latin tangere, «to touch».
History[edit]
Euclid makes several references to the tangent (ἐφαπτομένη ephaptoménē) to a circle in book III of the Elements (c. 300 BC).[3] In Apollonius’ work Conics (c. 225 BC) he defines a tangent as being a line such that no other straight line could
fall between it and the curve.[4]
Archimedes (c. 287 – c. 212 BC) found the tangent to an Archimedean spiral by considering the path of a point moving along the curve.[4]
In the 1630s Fermat developed the technique of adequality to calculate tangents and other problems in analysis and used this to calculate tangents to the parabola. The technique of adequality is similar to taking the difference between 


These methods led to the development of differential calculus in the 17th century. Many people contributed. Roberval discovered a general method of drawing tangents, by considering a curve as described by a moving point whose motion is the resultant of several simpler motions.[6]
René-François de Sluse and Johannes Hudde found algebraic algorithms for finding tangents.[7] Further developments included those of John Wallis and Isaac Barrow, leading to the theory of Isaac Newton and Gottfried Leibniz.
An 1828 definition of a tangent was «a right line which touches a curve, but which when produced, does not cut it».[8] This old definition prevents inflection points from having any tangent. It has been dismissed and the modern definitions are equivalent to those of Leibniz, who defined the tangent line as the line through a pair of infinitely close points on the curve.
Tangent line to a plane curve[edit]
The intuitive notion that a tangent line «touches» a curve can be made more explicit by considering the sequence of straight lines (secant lines) passing through two points, A and B, those that lie on the function curve. The tangent at A is the limit when point B approximates or tends to A. The existence and uniqueness of the tangent line depends on a certain type of mathematical smoothness, known as «differentiability.» For example, if two circular arcs meet at a sharp point (a vertex) then there is no uniquely defined tangent at the vertex because the limit of the progression of secant lines depends on the direction in which «point B» approaches the vertex.
At most points, the tangent touches the curve without crossing it (though it may, when continued, cross the curve at other places away from the point of tangent). A point where the tangent (at this point) crosses the curve is called an inflection point. Circles, parabolas, hyperbolas and ellipses do not have any inflection point, but more complicated curves do have, like the graph of a cubic function, which has exactly one inflection point, or a sinusoid, which has two inflection points per each period of the sine.
Conversely, it may happen that the curve lies entirely on one side of a straight line passing through a point on it, and yet this straight line is not a tangent line. This is the case, for example, for a line passing through the vertex of a triangle and not intersecting it otherwise—where the tangent line does not exist for the reasons explained above. In convex geometry, such lines are called supporting lines.
At each point, the moving line is always tangent to the curve. Its slope is the derivative; green marks positive derivative, red marks negative derivative and black marks zero derivative. The point (x,y) = (0,1) where the tangent intersects the curve, is not a max, or a min, but is a point of inflection.
Analytical approach[edit]
The geometrical idea of the tangent line as the limit of secant lines serves as the motivation for analytical methods that are used to find tangent lines explicitly. The question of finding the tangent line to a graph, or the tangent line problem, was one of the central questions leading to the development of calculus in the 17th century. In the second book of his Geometry, René Descartes[9] said of the problem of constructing the tangent to a curve, «And I dare say that this is not only the most useful and most general problem in geometry that I know, but even that I have ever desired to know».[10]
Intuitive description[edit]
Suppose that a curve is given as the graph of a function, y = f(x). To find the tangent line at the point p = (a, f(a)), consider another nearby point q = (a + h, f(a + h)) on the curve. The slope of the secant line passing through p and q is equal to the difference quotient
As the point q approaches p, which corresponds to making h smaller and smaller, the difference quotient should approach a certain limiting value k, which is the slope of the tangent line at the point p. If k is known, the equation of the tangent line can be found in the point-slope form:
More rigorous description[edit]
To make the preceding reasoning rigorous, one has to explain what is meant by the difference quotient approaching a certain limiting value k. The precise mathematical formulation was given by Cauchy in the 19th century and is based on the notion of limit. Suppose that the graph does not have a break or a sharp edge at p and it is neither plumb nor too wiggly near p. Then there is a unique value of k such that, as h approaches 0, the difference quotient gets closer and closer to k, and the distance between them becomes negligible compared with the size of h, if h is small enough. This leads to the definition of the slope of the tangent line to the graph as the limit of the difference quotients for the function f. This limit is the derivative of the function f at x = a, denoted f ′(a). Using derivatives, the equation of the tangent line can be stated as follows:
Calculus provides rules for computing the derivatives of functions that are given by formulas, such as the power function, trigonometric functions, exponential function, logarithm, and their various combinations. Thus, equations of the tangents to graphs of all these functions, as well as many others, can be found by the methods of calculus.
How the method can fail[edit]
Calculus also demonstrates that there are functions and points on their graphs for which the limit determining the slope of the tangent line does not exist. For these points the function f is non-differentiable. There are two possible reasons for the method of finding the tangents based on the limits and derivatives to fail: either the geometric tangent exists, but it is a vertical line, which cannot be given in the point-slope form since it does not have a slope, or the graph exhibits one of three behaviors that precludes a geometric tangent.
The graph y = x1/3 illustrates the first possibility: here the difference quotient at a = 0 is equal to h1/3/h = h−2/3, which becomes very large as h approaches 0. This curve has a tangent line at the origin that is vertical.
The graph y = x2/3 illustrates another possibility: this graph has a cusp at the origin. This means that, when h approaches 0, the difference quotient at a = 0 approaches plus or minus infinity depending on the sign of x. Thus both branches of the curve are near to the half vertical line for which y=0, but none is near to the negative part of this line. Basically, there is no tangent at the origin in this case, but in some context one may consider this line as a tangent, and even, in algebraic geometry, as a double tangent.
The graph y = |x| of the absolute value function consists of two straight lines with different slopes joined at the origin. As a point q approaches the origin from the right, the secant line always has slope 1. As a point q approaches the origin from the left, the secant line always has slope −1. Therefore, there is no unique tangent to the graph at the origin. Having two different (but finite) slopes is called a corner.
Finally, since differentiability implies continuity, the contrapositive states discontinuity implies non-differentiability. Any such jump or point discontinuity will have no tangent line. This includes cases where one slope approaches positive infinity while the other approaches negative infinity, leading to an infinite jump discontinuity
Equations[edit]
When the curve is given by y = f(x) then the slope of the tangent is
so by the point–slope formula the equation of the tangent line at (X, Y) is
where (x, y) are the coordinates of any point on the tangent line, and where the derivative is evaluated at 
When the curve is given by y = f(x), the tangent line’s equation can also be found[12] by using polynomial division to divide 


When the equation of the curve is given in the form f(x, y) = 0 then the value of the slope can be found by implicit differentiation, giving
The equation of the tangent line at a point (X,Y) such that f(X,Y) = 0 is then[11]
This equation remains true if 


For algebraic curves, computations may be simplified somewhat by converting to homogeneous coordinates. Specifically, let the homogeneous equation of the curve be g(x, y, z) = 0 where g is a homogeneous function of degree n. Then, if (X, Y, Z) lies on the curve, Euler’s theorem implies
It follows that the homogeneous equation of the tangent line is
The equation of the tangent line in Cartesian coordinates can be found by setting z=1 in this equation.[13]
To apply this to algebraic curves, write f(x, y) as
where each ur is the sum of all terms of degree r. The homogeneous equation of the curve is then
Applying the equation above and setting z=1 produces
as the equation of the tangent line.[14] The equation in this form is often simpler to use in practice since no further simplification is needed after it is applied.[13]
If the curve is given parametrically by
then the slope of the tangent is
giving the equation for the tangent line at 
If 
Normal line to a curve[edit]
The line perpendicular to the tangent line to a curve at the point of tangency is called the normal line to the curve at that point. The slopes of perpendicular lines have product −1, so if the equation of the curve is y = f(x) then slope of the normal line is
and it follows that the equation of the normal line at (X, Y) is
Similarly, if the equation of the curve has the form f(x, y) = 0 then the equation of the normal line is given by[16]
If the curve is given parametrically by
then the equation of the normal line is[15]
Angle between curves[edit]
The angle between two curves at a point where they intersect is defined as the angle between their tangent lines at that point. More specifically, two curves are said to be tangent at a point if they have the same tangent at a point, and orthogonal if their tangent lines are orthogonal.[17]
Multiple tangents at a point[edit]
The limaçon trisectrix: a curve with two tangents at the origin.
The formulas above fail when the point is a singular point. In this case there may be two or more branches of the curve that pass through the point, each branch having its own tangent line. When the point is the origin, the equations of these lines can be found for algebraic curves by factoring the equation formed by eliminating all but the lowest degree terms from the original equation. Since any point can be made the origin by a change of variables (or by translating the curve) this gives a method for finding the tangent lines at any singular point.
For example, the equation of the limaçon trisectrix shown to the right is
Expanding this and eliminating all but terms of degree 2 gives
which, when factored, becomes
So these are the equations of the two tangent lines through the origin.[18]
When the curve is not self-crossing, the tangent at a reference point may still not be uniquely defined because the curve is not differentiable at that point although it is differentiable elsewhere. In this case the left and right derivatives are defined as the limits of the derivative as the point at which it is evaluated approaches the reference point from respectively the left (lower values) or the right (higher values). For example, the curve y = |x | is not differentiable at x = 0: its left and right derivatives have respective slopes −1 and 1; the tangents at that point with those slopes are called the left and right tangents.[19]
Sometimes the slopes of the left and right tangent lines are equal, so the tangent lines coincide. This is true, for example, for the curve y = x 2/3, for which both the left and right derivatives at x = 0 are infinite; both the left and right tangent lines have equation x = 0.
Tangent line to a space curve[edit]
Tangent circles[edit]
Two pairs of tangent circles. Above internally and below externally tangent
Two circles of non-equal radius, both in the same plane, are said to be tangent to each other if they meet at only one point. Equivalently, two circles, with radii of ri and centers at (xi, yi), for i = 1, 2 are said to be tangent to each other if
- Two circles are externally tangent if the distance between their centres is equal to the sum of their radii.
- Two circles are internally tangent if the distance between their centres is equal to the difference between their radii.[20]
Tangent plane to a surface[edit]
«Tangent plane» redirects here. For the geographical concept, see Local tangent plane.
|
This section needs expansion. You can help by adding to it. (May 2022) |
The tangent plane to a surface at a given point p is defined in an analogous way to the tangent line in the case of curves. It is the best approximation of the surface by a plane at p, and can be obtained as the limiting position of the planes passing through 3 distinct points on the surface close to p as these points converge to p.
Higher-dimensional manifolds[edit]
More generally, there is a k-dimensional tangent space at each point of a k-dimensional manifold in the n-dimensional Euclidean space.
See also[edit]
- Newton’s method
- Normal (geometry)
- Osculating circle
- Osculating curve
- Perpendicular
- Subtangent
- Supporting line
- Tangent cone
- Tangential angle
- Tangential component
- Tangent lines to circles
- Tangent vector
- Multiplicity (mathematics)#Behavior of a polynomial function near a multiple root
- Algebraic curve#Tangent at a point
References[edit]
- ^ Leibniz, G., «Nova Methodus pro Maximis et Minimis», Acta Eruditorum, Oct. 1684.
- ^ Dan Sloughter (2000) . «Best Affine Approximations»
- ^ Euclid. «Euclid’s Elements». Retrieved 1 June 2015.
- ^ a b Shenk, Al. «e-CALCULUS Section 2.8» (PDF). p. 2.8. Retrieved 1 June 2015.
- ^ Katz, Victor J. (2008). A History of Mathematics (3rd ed.). Addison Wesley. p. 510. ISBN 978-0321387004.
- ^ Wolfson, Paul R. (2001). «The Crooked Made Straight: Roberval and Newton on Tangents». The American Mathematical Monthly. 108 (3): 206–216. doi:10.2307/2695381. JSTOR 2695381.
- ^ Katz, Victor J. (2008). A History of Mathematics (3rd ed.). Addison Wesley. pp. 512–514. ISBN 978-0321387004.
- ^ Noah Webster, American Dictionary of the English Language (New York: S. Converse, 1828), vol. 2, p. 733, [1]
- ^ Descartes, René (1954). The geometry of René Descartes. Courier Dover. p. 95. ISBN 0-486-60068-8.
- ^ R. E. Langer (October 1937). «Rene Descartes». American Mathematical Monthly. Mathematical Association of America. 44 (8): 495–512. doi:10.2307/2301226. JSTOR 2301226.
- ^ a b Edwards Art. 191
- ^ Strickland-Constable, Charles, «A simple method for finding tangents to polynomial graphs», Mathematical Gazette, November 2005, 466–467.
- ^ a b Edwards Art. 192
- ^ Edwards Art. 193
- ^ a b Edwards Art. 196
- ^ Edwards Art. 194
- ^ Edwards Art. 195
- ^ Edwards Art. 197
- ^ Thomas, George B. Jr., and Finney, Ross L. (1979), Calculus and Analytic Geometry, Addison Wesley Publ. Co.: p. 140.
- ^ «Circles For Leaving Certificate Honours Mathematics by Thomas O’Sullivan 1997».
Sources[edit]
- J. Edwards (1892). Differential Calculus. London: MacMillan and Co. pp. 143 ff.
External links[edit]
Wikimedia Commons has media related to Tangency.
- «Tangent line», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. «Tangent Line». MathWorld.
- Tangent to a circle With interactive animation
- Tangent and first derivative — An interactive simulation
Общие сведения
Важно знать терминологию, соотношения и теоремы для решения задач этого класса. Касательной к окружности называется прямая, которая имеет с ней только одну точку соприкосновения. Прямая — это линия, не имеющая границ, т. е. она ничем не ограничена. Окружностью называется геометрическое место точек, удаленных от центра на одинаковые расстояния.
Следует отметить, что касательные бывают внешними и внутренними. Внешней называет прямая линия, проходящая с внешней стороны окружности. Внутренние касательные пересекают отрезок, который соединяет центры двух окружностей. Последний тип прямых не существует, когда два круга пересекаются. Касательные нужно уметь правильно строить, поскольку от этого зависит правильность решения задачи.
Построение касательных
Для построения касательной к окружности следует на последней отметить произвольную точку. Затем необходимо через нее провести прямую. Нужно отметить, что у круга может быть несколько таких прямых. Когда даны две окружности, тогда можно проводить не только внешние, но и внутренние. Существует определенный алгоритм, по которому можно построить первый тип:
- Начертить 2 окружности с центрами в точках О1 и О2. При этом должно соблюдаться условие r1 > r2, где r1 и r2 — радиусы I и II соответственно.
- Нарисовать III окружность с центром в О1 и радиусом r3 = r1 — r2.
- Провести 2 касательные из точки О2 к III. Они параллельны искомым, поскольку радиусы I и II уменьшаются на r2.
Существует более простая модель построения таких прямых. Для этого следует начертить один круг, а затем отметить две произвольные точки на его противоположных сторонах. Далее начертить II круг, превышающий I по радиусу. Отметить на нем точки, воспользовавшись подобием, т. е. они должны быть в тех же местах, что и на I. Затем провести прямые, которые должны соприкасаться с I и II кругами только в одной точке.
Для построения внутренних касательных существует определенная методика. В интернете можно найти много информации. В одних источниках алгоритм построения является сложным, а в других — простым. Однако есть один метод, позволяющий осуществить данную операцию. Специалисты описали его на «понятном» языке для новичков. Суть методики заключается в следующем:
- Необходимо построить два круга, которые не пересекаются, с радиусами r1 и r2. Расстояния между ними должно составлять r1 + r2.
- Соединить их центры (середины) отрезком.
- Отметить на нем среднюю точку, которая делит его на две равные части.
- Через точку, полученную на третьем шаге методики, провести прямую. Она должна иметь только одну точку соприкосновения с I и II окружностями.
- Аналогично провести еще одну прямую.
- Искомые прямые являются внутренними касательными.
Далее нужно рассмотреть некоторые свойства, на основании которых можно решать задачи и доказывать геометрические тождества.
Основные свойства
Свойства — утверждения, полученные в результате доказательства теорем о касательной к окружности. Первые нет необходимости доказывать, поскольку об этом уже позаботились математики. Они выделяют всего 4 свойства касательных к окружности:
- Если провести из одной точки две касательные к некоторой окружности, то отрезки, лежащие на них, будут равны. Искомый угол будет делиться радиусом пополам.
- Любая касательная и радиус, проведенный к ее точке, образуют прямой угол. Справедливо и обратное утверждение: радиус, который проведен в точку касания, перпендикулярен данной прямой.
- Вся секущая, умноженная на свою внешнюю часть, равна квадрату расстояния касательной, которая проведена из общей с ней точки.
- Образованный угол между касательной и секущей, эквивалентен градусной мере угла, который опирается на образованную хорду.
Для рассмотрения I свойства необходимо начертить окружность с центром О1. Затем нужно отметить точку М вне окружности. Из М провести одну прямую, которая соприкасается с кругом в точке А. Такую же операцию следует проделать и для другой касательной. Точку соприкосновения назвать В. Отрезки АМ и ВМ равны между собой.
Если провести радиусы к точкам А и В, то можно сделать вывод, что углы являются прямыми. Чтобы понять третье свойство, необходимо начертить окружность и отметить некоторую точку М за ее пределами. После этого следует из искомой точки провести секущую и касательную. Первой называется прямая, проходящая через окружность и пересекающая ее в двух точках. Для касательной точку соприкосновения необходимо обозначить А. Тогда секущая пересекает круг в точках В (ближняя) и С (дальняя). В результате этого получается такое соотношение: АМ 2 = АВ * МС.
Когда для произвольной окружности существуют касательная и секущая, тогда между ними образуется некоторый угол.
Хорда, полученная в результате прохождения через окружность, образует также угол. Он опирается на искомую хорду и является вписанным. Следовательно, по свойству градусные меры углов равны между собой. Далее нужно разобрать частные случаи, на основании которых можно сделать вывод о количестве касательных.
Когда окружность вписана в ромб, тогда их точки касания нужно рассматривать по первому свойству. Радиус окружности можно найти по следующим формулам:
- Через диагонали (d1, d2) и сторону (a): r = (d1 * d2) / 4а.
- Только по диагоналям: r = (d1 * d2) / [(d1)^2 + (d2)^2]^(½).
Следует отметить, что у ромба две диагонали. Они различаются по размеру. Одна из них больше другой (d1 > d2).
Частные случаи
В некоторых задачах нужно определить количество касательных у двух окружностей. Можно выполнить ряд сложных и трудоемких доказательств. В результате этого будет потрачено много времени, а можно воспользоваться уже готовыми дополнительными свойствами:
- Четыре касательных: круги не соприкасаются, т. е. d > r1 + r2 (значение диаметра больше суммы радиусов r1 и r2).
- Две общие внешние и одна внутренняя: окружности соприкасаются только в одной точке (d = r1 + r2).
- Только две внешние: пересечение окружностей в двух точках (|r1 — r2| < d < r1 + r2).
- Одна общая внешняя: окружности касаются внутри друг друга (d = |r1 — r2|).
- Отсутствуют: один круг находится внутри другого (d < |r1 — r2|).
В последнем случае любая касательная будет являться секущей для другой окружности. Существует еще одно положение, когда окружности совпадают. Тогда любая касательная считается общей. В высшей математике разбирается также «отрицательный» радиус. Тогда вышеперечисленные свойства можно править следующим образом:
- Нет касательных: окружности не соприкасаются, и для них выполняется условие d < — (r1 + r2).
- Две внутренние (общие) и одна внешняя: круги соприкасаются в одной точке (d = -r1 — r2).
- Одна пара внутренних: пересечение в 2 точках (|r1 — r2| > d > — r1 — r2).
- Внутренняя общая (одна): соприкасаются внутри (d = |r2 — r1|).
- Четыре: при d > |r1 — r2|.
Когда заданы окружности, радиус одной из которых равен 0, тогда «нулевой» круг эквивалентен двойной точке. Прямая является двойной и проходит через эту точку. В этом случае математики определяют всего две внешних. Если r1 = r2 = 0, то всего 4 внешних общих касательных. Далее для решения задач нужно разобрать доказательства некоторых свойств.
Доказательства утверждений
Очень важно знать доказательства некоторых свойств и теорем, поскольку одним из типов задач считаются упражнения повышенной сложности, требующие логических расчетов в общем виде. Например, нужно доказать, что касательная образует с радиусом, проведенным к точке касания, прямой угол. Существует тип доказательства от противного.
Для этого следует предположить, что искомый угол не равен 90 градусам. Пусть дана некоторая касательная р. Она имеет с кругом общую точку А. Нужно провести к ней перпендикуляр (радиус). Далее нужно провести из центра О отрезок ОВ на р. Образуется прямоугольный треугольник АВО с гипотенузой ОВ. Если опираться на утверждение от противного, то гипотенуза будет меньше катета (d < r). Однако радиус не может быть больше диаметра, поскольку он рассчитывается по следующей формуле: d = 2 * r. Следовательно, утверждение доказано.
Аналогично доказывается и обратное свойство. Его формулировка имеет такой вид: прямая, проходящая под прямым углом через точку, которая образована радиусом, является касательной. В этом случае можно доказывать не от противного. Расстояние от прямой до центра окружности эквивалентно некоторой величине и является радиусом. Из определения следует, что прямая и окружность имеют общую точку, и только одну. Следовательно, она и есть касательная.
Доказательство об отрезках, проведенных из одной точки, тоже нужно разобрать, поскольку такой прием применяется в решении сложных задач. Отрезки равны между собой и образуют с прямой, проведенной к центру круга, эквивалентные углы.
Следует выполнить построение окружности с центром Р. Далее нужно обозначить точку А за ее пределами и провести из нее лучи-касательные к искомой окружности. Они образуют на круге точки А и В. Кроме того, следует доказать равенство углов ОАВ и САО. При построении образовалось два треугольника ОВА и ОСА. Фигуры являются прямоугольными на основании свойства о касательной и радиусе.
Далее необходимо доказать равенство фигур ОВА и ОСА. Это сделать довольно просто: гипотенуза — общая, катеты ОВ и ОС равны (радиусы) и углы АВО = АСО = 90. Следовательно, они равны по первому признаку, а также эквивалентны друг другу стороны АВ и АС. Кроме того, угол ОАВ = САО. Утверждение доказано. Гипотенуза является также и биссектрисой. В некоторых источниках можно встретить доказательство равенства тангенсов углов.
Пример решения задачи
Нужно составить уравнения касательных к окружности (описанной графиком функции х 2 + y 2 = 2x + 6y + 19), проходящих через координаты х =0 у= -14. Для решения задачи следует действовать по такому алгоритму:
- Перенести все слагаемые, кроме 19, в левую сторону: х 2 + y 2 — 2x — 6y = 19.
- Выделить полный квадрат для окончательной записи уравнения окружности: х 2 — 2x + 1 — 1 + y 2 — 6y +9 — 9 = (х — 1)^2 + (y — 3)^2 = 29.
- Уравнение прямой, проходящей через (0;-14) в общем виде: y — (-14) = k * (x — 0) или у = кх — 14.
- Составить систему уравнений: (х — 1)^2 + (y — 3)^2 = 29 и у = кх — 14.
- Подставить второе в первое: (х — 1)^2 + (кх — 14 — 3)^2 = 29.
- Упростить выражение: (х — 1)^2 + (кх — 14 — 3)^2 — 29 = х 2 — 2x + 1 +k 2 * x 2 — 34kx + 289 — 29 = (1 + k 2 ) * x 2 — 2 * (17k + 1) + 261.
- Решением уравнения должен быть один корень: D/4 = 0.
- Упростить тождество: D/4 = (-(17k + 1))^2 — 261 (1 + k 2 ) = 289k 2 + 34k + 1 — 261 — 261k 2 = 28k 2 + 34k — 260 = 0.
- Найти значение D: 17 2 — 28 * (-260) = 289 + 7280 = 7569.
- Первый коэффициент к1 = (-17 — 87) / 28 = -26/7.
- Коэффициент к2 = (-17 + 87) / 28 = 5/2.
- Записать уравнения прямых с учетом к1 и к2: у1 = (-26/7) * х — 14 (26х + 7у + 98 = 0) и у2 = (5/2) * х — 14 (5х — 2у — 28 = 0).
Следует отметить, что уравнение окружности с радиусом, равным единице, описывается функцией x2 + y 2 = 1. Эта запись применяется для решения задач в общем виде. Прямая — функция, описанная прямой пропорциональностью у = кх + b. Чтобы связать окружность и касательные, нужно составить систему уравнений. Этот математический ход объясняется тем, что у функций должны быть общие решения (точка на окружности). После решения можно выполнить проверочные вычисления, подставив корни в систему.
Таким образом, для решения задач об окружности и касательной следует знать общие понятия, а также основные свойства и теоремы.
Что такое касательная к окружности
8 июля 2018
- Домашняя работа
- Ответы и решения
Определение. Касательная к окружности — это прямая на плоскости, имеющая ровно одну общую точку с окружностью.
Вот парочка примеров:
На этом можно было бы закончить, однако практика показывает, что недостаточно просто зазубрить определение — нужно научиться видеть касательные на чертежах, знать их свойства и вдобавок как следует попрактиковаться в применении этих свойств, решая реальные задачи. Всем этим всем мы сегодня и займёмся.
Основные свойства касательных
Для того, чтобы решать любые задачи, нужно знать четыре ключевых свойства. Два из них описаны в любом справочнике / учебнике, а вот последние два — про них как-то забывают, а зря.
1. Отрезки касательных, проведённых из одной точки, равны
Чуть выше мы уже говорили про две касательных, проведённых из одной точки M. Так вот:
Отрезки касательных к окружности, проведённых из одной точки, равны.
2. Касательная перпендикулярна радиусу, проведённому в точку касания
Ещё раз посмотрим на картинку, представленную выше. Проведём радиусы OAи OB, после чего обнаружим, что углы OAMи OBM — прямые.
Радиус, проведённый в точку касания, перпендикулярен касательной.
Этот факт можно использовать без доказательства в любой задаче:
Кстати, заметьте: если провести отрезок OM, то мы получим два равных треугольника: OAM и OBM.
3. Соотношение между касательной и секущей
А вот это уже факт посерьёзнее, и большинство школьников его не знают. Рассмотрим касательную и секущую, которые проходят через одну и ту же общую точку M. Естественно, секущая даст нам два отрезка: внутри окружности (отрезок BC — его ещё называют хордой) и снаружи (его так и называют — внешняя часть MC).
Произведение всей секущей на её внешнюю часть равно квадрату отрезка касательной
4. Угол между касательной и хордой
Ещё более продвинутый факт, который часто используется для решения сложных задач. Очень рекомендую взять на вооружение.
Угол между касательной и хордой равен вписанному углу, опирающемуся на эту хорду.
Откуда берётся точка B? В реальных задачах она обычно «всплывает» где-то в условии. Поэтому важно научиться распознавать данную конфигурацию на чертежах.

Смотрите также:
- Вписанный угол в геометрии
- Задачи B12, сводящиеся к линейным уравнениям
- Геометрическая вероятность
- Задача 18: метод симметричных корней
- Задача B2 про комиссию в терминале
- Значение тригонометрических функций
Касательная
- Касательная
-
График функции (чёрная кривая) и касательная прямая (красная прямая)
Каса́тельная пряма́я — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.
Содержание
- 1 Определение
- 2 Замечание
- 3 Касательная как предельное положение секущей
- 4 Касательная к окружности
- 4.1 Свойства
- 5 Вариации и обобщения
- 5.1 Односторонние полукасательные
- 6 См. также
Определение
Замечание
Прямо из определения следует, что график касательной прямой проходит через точку (x0,f(x0)). Угол α между касательной к кривой и осью Ох удовлетворяет уравнению
где
обозначает тангенс, а
— коэффициент наклона касательной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
Касательная как предельное положение секущей
Пусть
и
Тогда прямая линия, проходящая через точки (x0,f(x0)) и (x1,f(x1)) задаётся уравнением
Эта прямая проходит через точку (x0,f(x0)) для любого
и её угол наклона α(x1) удовлетворяет уравнению
В силу существования производной функции f в точке x0, переходя к пределу при
получаем, что существует предел
а в силу непрерывности арктангенса и предельный угол
Прямая, проходящая через точку (x0,f(x0)) и имеющая предельный угол наклона, удовлетворяющий
задаётся уравнением касательной:
- y = f(x0) + f‘(x0)(x − x0).
Касательная к окружности
Отрезки касательных
Прямая, имеющая одну общую точку с окружностью и лежащая с ней в одной плоскости, называется касательной к окружности.
Свойства
- Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
- Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
- Длина отрезка касательной, проведённой к окружности единичного радиуса, взятого между точкой касания и точкой пересечения касательной с радиусом, является тангенсом угла между этим радиусом и направлением от центра окружности на точку касания. «Тангенс» от лат. tangens — «касательная».
Вариации и обобщения
Односторонние полукасательные
- Если существует правая производная
то пра́вой полукаса́тельной к графику функции f в точке x0 называется луч
- Если существует левая производная
то ле́вой полукаса́тельной к графику функции f в точке x0 называется луч
- Если существует бесконечная правая производная
то правой полукасательной к графику функции f в точке x0 называется луч
- Если существует бесконечная левая производная
то правой полукасательной к графику функции f в точке x0 называется луч
См. также
- Дифференцируемая функция
- Касательное пространство
- Нормаль, бинормаль
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Касательная» в других словарях:
-
Касательная — Касательная. КАСАТЕЛЬНАЯ прямая к кривой l в точке M, предельное положение MT, к которому стремится секущая MM’ при приближении точки M’ к точке M. … Иллюстрированный энциклопедический словарь
-
КАСАТЕЛЬНАЯ — прямая к кривой L в точке M предельное положение (на рисунке MT), к которому стремится секущая ММ? при приближении точки М? к точке М … Большой Энциклопедический словарь
-
КАСАТЕЛЬНАЯ — КАСАТЕЛЬНАЯ, касательной, жен. (мат.). Прямая линия, имеющая одну общую точку с кривой. Провести касательную к кругу. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
-
касательная — КАСАТЕЛЬНЫЙ, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
-
Касательная — прямая, с которою стремится совпасть секущая,проведенная через две точки на произвольной кривой, по мере сближенияэтих точек. Математическая теория К. имеет весьма важное значение.Точка, через которую к кривой линии проведена К., называется… … Энциклопедия Брокгауза и Ефрона
-
касательная — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN tangent … Справочник технического переводчика
-
Касательная — к кривой линии, предельное положение секущей. К. определяется так. Пусть М точка кривой L (рис. 1). Выберем на L вторую точку M и проведём прямую MM . Будем считать М неподвижной, а точку M приближать к М по кривой L. Если при… … Большая советская энциклопедия
-
касательная — ой; ж. Матем. Прямая, имеющая общую точку с кривой, но не пересекающая её. Провести касательную к окружности. * * * касательная прямая к кривой L в точке М, предельное положение (на рисунке МТ), к которому стремится секущая ММ при приближении… … Энциклопедический словарь
-
КАСАТЕЛЬНАЯ — прямая к кривой в точке М предельное положение (на рис. МТ), к к рому стремится секушая ММ при приближении точки М к точке М. К ст. Касательная … Большой энциклопедический политехнический словарь
-
КАСАТЕЛЬНАЯ — прямая к кривой L в точке М; предельное положение (на рис. МТ), к к рому стремится секущая ММ при приближении точки М к точке М … Естествознание. Энциклопедический словарь
Касательно кривой. Красная линия касается кривой в точке, отмеченной красной точкой.
Касательная плоскость к сфере
В геометрия, то касательная линия (или просто касательная) в самолет изгиб при данном точка это прямая линия это «просто касается» кривой в этой точке. Лейбниц определил его как линию, проходящую через пару бесконечно близко точки на кривой.[1] Точнее говоря, прямая линия называется касательной к кривой у = ж(Икс) в какой-то момент Икс = c если линия проходит через точку (c, ж(c)) на кривой и имеет наклон ж‘(c), куда ж‘ это производная из ж. Аналогичное определение применяется к космические кривые и кривые в п-размерный Евклидово пространство.
Когда он проходит через точку пересечения касательной и кривой, называется точка касания, касательная линия «идет в том же направлении», что и кривая, и, таким образом, является наилучшим приближением прямой к кривой в этой точке.
Точно так же касательная плоскость к поверхность в данный момент самолет это «просто касается» поверхности в этой точке. Понятие касательной — одно из самых фундаментальных понятий в дифференциальная геометрия и был широко обобщен; видеть Касательное пространство.
Слово «касательная» происходит от латинский тангере, «трогать».
История
Евклид делает несколько ссылок на касательную (ἐφαπτομένη ephaptoménē) к кругу в книге III Элементы (ок. 300 г. до н. э.).[2] В Аполлоний работай Коники (ок. 225 г. до н.э.) он определяет касательную как такая линия, что никакая другая прямая линия не можетупасть между ним и кривой.[3]
Архимед (ок. 287 — ок. 212 г. до н. э.) нашел касательную к Архимедова спираль рассматривая путь точки, движущейся по кривой.[3]
В 1630-е гг. Ферма разработал технику адекватность для вычисления касательных и других задач анализа и использовал это для вычисления касательных к параболе. Техника адекватности аналогична измерению разницы между 


Эти методы привели к развитию дифференциальное исчисление в 17-го века. Многие внесли свой вклад. Роберваль открыл общий метод рисования касательных, рассматривая кривую, описываемую движущейся точкой, движение которой является результатом нескольких более простых движений.[5]Рене-Франсуа де Слюз и Йоханнес Худде нашел алгебраические алгоритмы нахождения касательных.[6] Дальнейшие разработки включали в себя Джон Уоллис и Исаак Барроу, что привело к теории Исаак Ньютон и Готфрид Лейбниц.
Определение касательной в 1828 году было «прямой линией, которая касается кривой, но не пересекает ее».[7] Это старое определение предотвращает точки перегиба от касательной. Он был отклонен, и современные определения эквивалентны определениям Лейбниц кто определил касательную как линию, проходящую через пару бесконечно близко точки на кривой.
Касательная линия к кривой
Интуитивное представление о том, что касательная линия «касается» кривой, можно сделать более явным, если рассмотреть последовательность прямых линий (секущие линии ) проходя через две точки, А и B, лежащие на функциональной кривой. Касательная в А это предел, когда точка B приближается или стремится к А. Существование и уникальность касательной зависит от определенного типа математической гладкости, известного как «дифференцируемость». Например, если две дуги окружности пересекаются в острой точке (вершине), то в вершине нет однозначно определенной касательной, поскольку предел движения секущих линий зависит от направления, в котором «точка» B«приближается к вершине.
В большинстве точек касательная касается кривой, не пересекая ее (хотя при продолжении может пересекать кривую в других местах, удаленных от точки касания). Точка, где касательная (в этой точке) пересекает кривую, называется точка перегиба. Круги, параболы, гиперболы и эллипсы не имеют точки перегиба, но есть более сложные кривые, такие как график кубическая функция, который имеет ровно одну точку перегиба, или синусоиду, имеющую по две точки перегиба на каждую период из синус.
И наоборот, может случиться так, что кривая целиком лежит на одной стороне прямой линии, проходящей через точку на ней, и все же эта прямая линия не является касательной. Так обстоит дело, например, с прямой, проходящей через вершину треугольник и не пересекать его в противном случае — где касательная линия не существует по причинам, объясненным выше. В выпуклая геометрия такие линии называются поддерживающие линии.
В каждой точке движущаяся линия всегда касается изгиб. Его наклон — это производная; зеленый цвет обозначает положительную производную, красный обозначает отрицательную производную, а черный обозначает нулевую производную. Точка (x, y) = (0,1), где касательная пересекает кривую, не является Максимум, или мин, но это точка перегиба.
Аналитический подход
Геометрическая идея касательной линии как предела секущих служит мотивацией для аналитических методов, которые используются для явного нахождения касательных линий. Вопрос о нахождении касательной к графику или задача касательной, был одним из центральных вопросов, приведших к развитию исчисление в 17 веке. Во второй книге его Геометрия, Рене Декарт[8] сказал о проблеме построения касательной к кривой: «И я осмеливаюсь сказать, что это не только самая полезная и самая общая проблема геометрии, которую я знаю, но даже то, что я когда-либо хотел знать».[9]
Интуитивное описание
Предположим, что кривая задана как график функция, у = ж(Икс). Чтобы найти касательную в точке п = (а, ж(а)), рассмотрим еще одну ближайшую точку q = (а + час, ж(а + час)) на кривой. В склон из секущая линия проходя через п и q равно коэффициент разницы
Как точка q подходы п, что соответствует выполнению час все меньше и меньше, коэффициент разницы должен приближаться к определенному предельному значению k, который представляет собой наклон касательной в точке п. Если k Как известно, уравнение касательной можно найти в форме точка-наклон:
Более точное описание
Чтобы сделать предыдущее рассуждение строгим, необходимо объяснить, что подразумевается под коэффициентом разности, приближающимся к определенному предельному значению. k. Точная математическая формулировка была дана Коши в 19 веке и основан на представлении о предел. Предположим, что граф не имеет излома или острого ребра в точке п И это не отвесно и не слишком близко п. Тогда есть уникальное значение k так что, как час приближается к 0, коэффициент разницы становится все ближе и ближе к k, и расстояние между ними становится ничтожным по сравнению с размером час, если час достаточно мала. Это приводит к определению наклона касательной к графику как предела разностных отношений для функции ж. Этот предел является производная функции ж в Икс = а, обозначенный ж ′(а). Используя производные, уравнение касательной можно сформулировать следующим образом:
Исчисление предоставляет правила для вычисления производных функций, которые задаются формулами, такими как степенная функция, тригонометрические функции, экспоненциальная функция, логарифм, и их различные комбинации. Таким образом, уравнения касательных к графикам всех этих функций, как и многих других, могут быть найдены методами исчисления.
Как метод может потерпеть неудачу
Расчет также показывает, что на их графиках есть функции и точки, для которых не существует предела, определяющего наклон касательной. Для этих точек функция ж является недифференцируемый. Есть две возможные причины того, что метод нахождения касательных на основе пределов и производных не сработает: либо геометрическая касательная существует, но это вертикальная линия, которую нельзя представить в форме точечного наклона, поскольку у нее нет slope, или график демонстрирует одно из трех поведений, исключающих геометрический касательный.
График у = Икс1/3 иллюстрирует первую возможность: здесь коэффициент разности при а = 0 равно час1/3/час = час−2/3, который становится очень большим при час стремится к 0. Эта кривая имеет вертикальную касательную в начале координат.
График у = Икс2/3 иллюстрирует другую возможность: этот график имеет куспид в происхождении. Это означает, что когда час стремится к 0, коэффициент разности при а = 0 приближается к плюс или минус бесконечности в зависимости от знака Икс. Таким образом, обе ветви кривой находятся рядом с полувертикальной линией, для которой у= 0, но нет рядом с отрицательной частью этой линии. По сути, в этом случае нет касательной в начале координат, но в некотором контексте можно рассматривать эту прямую как касательную, и даже в алгебраическая геометрия, как двойной касательный.
График у = |Икс| из абсолютная величина Функция состоит из двух прямых линий с разными наклонами, соединенных в начале координат. Как точка q приближается к началу координат справа, секущая всегда имеет наклон 1. Как точка q приближается к началу координат слева, секущая всегда имеет наклон −1. Следовательно, нет единственной касательной к графу в начале координат. Наличие двух разных (но конечных) уклонов называется угол.
Наконец, поскольку дифференцируемость предполагает непрерывность, контрапозитивный состояния прерывность подразумевает недифференцируемость. Любой такой скачок или точечный разрыв не будет иметь касательной. Это включает в себя случаи, когда один наклон приближается к положительной бесконечности, а другой — к отрицательной бесконечности, что приводит к бесконечному разрыву скачка.
Уравнения
Когда кривая задается у = ж(Икс), то наклон касательной равен 
куда (Икс, у) — координаты любой точки на касательной, и где производная вычисляется в 
Когда кривая задается у = ж(Икс) уравнение касательной также можно найти[11] используя полиномиальное деление делить 


Когда уравнение кривой задано в виде ж(Икс, у) = 0, то значение наклона можно найти по формуле неявное дифференцирование, давая
Уравнение касательной в точке (Икс,Y) такие, что ж(Икс,Y) = 0 тогда[10]
Это уравнение остается верным, если 


За алгебраические кривые, вычисления можно несколько упростить, преобразовав в однородные координаты. В частности, пусть однородное уравнение кривой имеет вид грамм(Икс, у, z) = 0 где грамм является однородной функцией степени п. Тогда, если (Икс, Y, Z) лежит на кривой, Теорема Эйлера подразумевает
Отсюда следует, что однородное уравнение касательной имеет вид
Уравнение касательной в декартовых координатах можно найти, задав z= 1 в этом уравнении.[12]
Чтобы применить это к алгебраическим кривым, напишите ж(Икс, у) в качестве
где каждый тыр это сумма всех членов степени р. Тогда однородное уравнение кривой имеет вид
Применение приведенного выше уравнения и установка z= 1 производит
как уравнение касательной.[13] Уравнение в этой форме часто проще использовать на практике, поскольку после его применения не требуется дальнейшего упрощения.[12]
Если кривая задана параметрически к
то наклон касательной равен
давая уравнение касательной в точке 
Если 
Нормальная линия к кривой
Прямая, перпендикулярная касательной к кривой в точке касания, называется прямой. нормальная линия к кривой в этой точке. Наклоны перпендикулярных прямых имеют произведение −1, поэтому, если уравнение кривой имеет вид у = ж(Икс), то наклон нормальной линии равен
и отсюда следует, что уравнение нормальной прямой в точке (X, Y) имеет вид
Аналогично, если уравнение кривой имеет вид ж(Икс, у) = 0, то уравнение нормальной прямой имеет вид[15]
Если кривая задана параметрически как
тогда уравнение нормальной линии имеет вид[14]
Угол между кривыми
Угол между двумя кривыми в точке их пересечения определяется как угол между их касательными в этой точке. Более конкретно, две кривые называются касательными в точке, если они имеют одинаковую касательную в точке, и ортогональными, если их касательные линии ортогональны.[16]
Множественные касательные в точке
Трисектриса лимака: кривая с двумя касательными в начале координат.
Формулы выше не работают, если точка особая точка. В этом случае через точку могут проходить две или более ветви кривой, каждая из которых имеет свою касательную линию. Когда точка является началом координат, уравнения этих линий могут быть найдены для алгебраических кривых путем факторизации уравнения, образованного путем исключения всех членов, кроме членов самой низкой степени из исходного уравнения. Поскольку любая точка может быть сделана началом координат заменой переменных (или Идет перевод кривая), что дает метод нахождения касательных в любой особой точке.
Например, уравнение Limaçon Triisectrix справа показано
Расширение этого и исключение всех, кроме членов степени 2, дает
который после факторинга становится
Итак, это уравнения двух касательных, проходящих через начало координат.[17]
Когда кривая не является самопересекающейся, касательная в контрольной точке все же может быть не определена однозначно, потому что кривая не дифференцируема в этой точке, хотя она дифференцируема в другом месте. В этом случае левая и правая производные определяются как пределы производной, поскольку точка, в которой она оценивается, приближается к контрольной точке соответственно слева (более низкие значения) или справа (более высокие значения). Например, кривая у = |Икс | не дифференцируема в Икс = 0: его левая и правая производные имеют наклоны -1 и 1 соответственно; касательные в этой точке с этими уклонами называются левой и правой касательной.[18]
Иногда наклоны левой и правой касательных равны, поэтому касательные совпадают. Это верно, например, для кривой у = Икс 2/3, для которого и левая, и правая производные при Икс = 0 бесконечны; и левая, и правая касательные имеют уравнение Икс = 0.
Касательные круги
Две пары касательных окружностей. Сверху внутри и снизу снаружи по касательной
Два круга неравного радиуса, оба в одной плоскости, называются касательными друг к другу, если они встречаются только в одной точке. Эквивалентно два круги, с радиусы из ря и центры в (Икся, уя), за я = 1, 2 называются касательными друг к другу, если
- Два круга внешне касательный если расстояние между их центрами равна сумме их радиусов.
- Два круга внутренне касательный если расстояние между их центрами равна разнице их радиусов.[19]
Поверхности и многомерные многообразия
В касательная плоскость к поверхность в данный момент п определяется аналогично касательной в случае кривых. Это наилучшее приближение поверхности плоскостью при п, и может быть получено как предельное положение плоскостей, проходящих через 3 различных точки на поверхности, близких к п поскольку эти точки сходятся к п. В более общем плане существует k-размерный касательное пространство в каждой точке k-размерный многообразие в п-размерный Евклидово пространство.
Смотрите также
- Метод Ньютона
- Нормальный (геометрия)
- Оскулирующий круг
- Оскулирующая кривая
- Перпендикуляр
- Подкасательная
- Линия поддержки
- Касательный конус
- Тангенциальный угол
- Тангенциальная составляющая
- Касательные линии к окружностям
- Кратность (математика) # Поведение полиномиальной функции около кратного корня
- Алгебраическая кривая # Касательная в точке
Рекомендации
- ^ Лейбниц, Г. «Nova Methodus pro Maximis et Minimis «, Acta Eruditorum, Октябрь 1684 г.
- ^ Евклид. «Элементы Евклида». Получено 1 июня 2015.
- ^ а б Шенк, Ал. «e-CALCULUS Раздел 2.8» (PDF). п. 2,8. Получено 1 июня 2015.
- ^ Кац, Виктор Дж. (2008). История математики (3-е изд.). Эддисон Уэсли. п. 510. ISBN 978-0321387004.
- ^ Вольфсон, Пол Р. (2001). «Кривое, сделанное прямо: Роберваль и Ньютон на касательных». Американский математический ежемесячник. 108 (3): 206–216. Дои:10.2307/2695381.
- ^ Кац, Виктор Дж. (2008). История математики (3-е изд.). Эддисон Уэсли. С. 512–514. ISBN 978-0321387004.
- ^ Ной Вебстер, Американский словарь английского языка (Нью-Йорк: С. Конверс, 1828), т. 2, стр. 733, г. [1]
- ^ Декарт, Рене (1954). Геометрия Рене Декарта. Курьер Дувр. п. 95. ISBN 0-486-60068-8.
- ^ Р. Э. Лангер (октябрь 1937 г.). «Рене Декарт». Американский математический ежемесячный журнал. Математическая ассоциация Америки. 44 (8): 495–512. Дои:10.2307/2301226. JSTOR 2301226.
- ^ а б Эдвардс Искусство. 191
- ^ Стрикленд-Констебль, Чарльз, «Простой метод нахождения касательных к полиномиальным графам», Математический вестник, Ноябрь 2005 г., 466–467.
- ^ а б Эдвардс Искусство. 192
- ^ Эдвардс Искусство. 193
- ^ а б Эдвардс Искусство. 196
- ^ Эдвардс Искусство. 194
- ^ Эдвардс Искусство. 195
- ^ Эдвардс Искусство. 197
- ^ Томас, Джордж Б. младший, и Финни, Росс Л. (1979), Исчисление и аналитическая геометрия, Addison Wesley Publ. Co .: p. 140.
- ^ Кружки для получения аттестата с отличием по математике Томаса О’Салливана 1997
Источники
- Дж. Эдвардс (1892). Дифференциальное исчисление. Лондон: MacMillan and Co., стр.143 ff.
внешняя ссылка
- «Касательная линия», Энциклопедия математики, EMS Press, 2001 [1994]
- Вайсштейн, Эрик В. «Касательная линия». MathWorld.
- По касательной к кругу С интерактивной анимацией
- Касательная и первая производная — Интерактивное моделирование
Касательная к окружности
Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.
Расскажем подробнее, что такое касательная и секущая.
Напомним, что расстояние от точки до прямой — это длина перпендикуляра, опущенного из точки на прямую.
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая является касательной к окружности. В этом случае она имеет с окружностью ровно одну общую точку. Такую прямую называют касательной к окружности.
Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая пересекает окружность в двух точках. Такую прямую называют секущей.
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая не имеет с окружностью общих точек.
Запишем основные теоремы о касательных. Они помогут нам при решении задач ЕГЭ и ОГЭ.
Теорема 1.
Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
На рисунке радиус OA перпендикулярен прямой m.
Теорема 2. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Доказательство:
Дана окружность с центром O.
Прямые AB и AC — касательные, точки B и C — точки касания. Докажем, что
AB = AC и
Проведем радиусы OB и OC в точки касания.
По свойству касательной, и
.
В прямоугольных треугольниках AOB и AOC катеты OB и OC равны как радиусы одной окружности, AO — общая гипотенуза. Следовательно, треугольники AOB и AOC равны по гипотенузе и катету. Отсюда AB = AC и
Теорема 3. Отрезки касательных, проведенных к окружности из одной точки, равны.
Доказательство:
Пусть из точки A к окружности проведены касательные AB и AC. Соединим точку A с центром окружности точкой O. Треугольники AOB и AOC равны по гипотенузе и катету, следовательно, AB = AC.
Теорема 4. Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
Угол ACМ на рисунке равен половине угловой величины дуги AC.
Доказательство теоремы здесь.
Теорема 5, о секущей и касательной.
Если из одной точки к окружности проведены секущая и касательная, то произведение всей секущей на ее внешнюю часть равно квадрату отрезка касательной.
Доказательство теоремы смотрите здесь.
Разберем задачи ЕГЭ и ОГЭ по теме: Касательная к окружности.
Задача 1.
Угол ACO равен , где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.
Решение:
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, угол CAO — прямой. Из треугольника ACO получим, что угол AOC равен 62 градуса. Bеличина центрального угла равна угловой величине дуги, на которую он опирается, значит, величина дуги AB— тоже 62 градуса.
Ответ: 62.
Задача 2.
Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна . Ответ дайте в градусах.
Решение:
Это чуть более сложная задача. Центральный угол AOD опирается на дугу AD, следовательно, он равен 116 градусов. Тогда угол AOC равен Касательная перпендикулярна радиусу, проведенному в точку касания, значит, угол OAC — прямой. Тогда угол ACO равен
Ответ: 26.
Задача 3.
Хорда AB стягивает дугу окружности в Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
Решение:
Проведем радиус OB в точку касания, а также радиус OA. Угол OBC равен Треугольник BOA — равнобедренный. Нетрудно найти, что угол OBA равен 44 градуса, и тогда угол CBA равен 46 градусов, то есть половине угловой величины дуги AB.
Мы могли также воспользоваться теоремой: Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
Задача 4.
К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
Решение:
Вспомним еще одно важное свойство касательных к окружности:
Отрезки касательных, проведенных из одной точки, равны.
Периметр треугольника — это сумма всех его сторон. Обратите внимание на точки на нашем чертеже, являющиеся вершинами шестиугольника. Из каждой такой точки проведены два отрезка касательных к окружности. Отметьте на чертеже такие равные отрезки. Еще лучше, если одинаковые отрезки вы будете отмечать одним цветом. Постарайтесь увидеть, как периметр треугольника ABC складывается из периметров отсеченных треугольников.
Ответ: 24.
Вот более сложная задача из вариантов ЕГЭ:
Задача 5.
Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.
Решение:
Обратите внимание — в условии даже не сказано, сколько сторон у этого многоугольника. Видимо, это неважно. Пусть их будет пять, как на рисунке.
Окружность касается всех сторон многоугольника. Отметьте центр окружности — точку O — и проведите перпендикулярные сторонам радиусы в точки касания.
Соедините точку O с вершинами A, B, C, D, E. Получились треугольники AOB, BOC, COD, DOE и EOA.
Очевидно, что площадь многоугольника
Треугольники АОВ, ВОС, COD, DOE и ЕОА имеют равные высоты, причем все эти высоты равны радиусу окружности.
где p — полупериметр многоугольника.
По условию, P = 10, S = 5, тогда
Ответ: 1
Задачи ЕГЭ
1. Угол ACO равен , где O — центр окружности. Его сторона CA касается окружности. Сторона CO пересекает окружность в точке B . Найдите величину меньшей дуги AB окружности. Ответ дайте в градусах.
Решение:
По условию, CA — касательная, A — точка касания.
. Треугольник ACO — прямоугольный,
.
Угол — центральный, и он равен угловой величине дуги AB, на которую опирается. Значит, градусная мера дуги AB равна
. Это меньшая дуга AB, а большая — с другой стороны от точек A и B, и она больше 180 градусов.
Ответ: 63.
2. Через концы A и B дуги окружности с центром O проведены касательные AC и BC. Меньшая дуга AB равна . Найдите угол ACB. Ответ дайте в градусах.
Решение:
Центральный угол AOB равен угловой величине дуги, на которую он опирается, то есть
AC и BC — касательные, поэтому , поскольку касательная перпендикулярна радиусу, проведенному в точку касания.
Сумма углов четырехугольника ACBO равна
Ответ: 122.
3. Хорда AB стягивает дугу окружности в . Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
Решение:
Применим теорему об угле между касательной и хордой.
Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.
Значит, угол ABC равен .
Ответ: 46.
4. Через концы A и B дуги окружности с центром О проведены касательные AC и BC. Угол CAB равен . Найдите угол AOB. Ответ дайте в градусах.
Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.
Поэтому меньшая дуга AB окружности равна . Центральный угол равен угловой величине дуги, на которую он опирается, значит, угол AOB равен
.
Мы могли бы решить задачу и по-другому, рассматривая четырехугольник ACBO, как в задаче 2.
Ответ: 64.
5. Через концы A, B дуги окружности в проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.
Решение:
Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними. В треугольнике ABC:
Ответ: 118.
6. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, сторона CO пересекает окружность в точках B и D, а дуга AD окружности, заключенная внутри этого угла, равна . Ответ дайте в градусах.
Решение:
По условию, DB — диаметр окружности, поэтому дуга AВ, не содержащая точки D, равна . На эту дугу опирается центральный угол AOB, он равен
. Треугольник AOC прямоугольный, так как касательная CA перпендикулярна радиусу ОA, проведенному в точку касания.
Ответ: 26.
Задачи ОГЭ по теме: Касательная к окружности
1. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.
Решение:
Отрезок OB — радиус, проведённый в точку касания, поэтому AB и OB перпендикулярны, треугольник AOB — прямоугольный. По теореме Пифагора:
Ответ: 5.
2. Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный . Найдите величину угла OMK. Ответ дайте в градусах.
Решение:
Касательная перпендикулярна радиусу, проведенному в точку касания, поэтому угол OКD — прямой. Тогда Треугольник OMK — равнобедренный, его стороны OК и OМ являются радиусами окружности, поэтому
Ответ: 7.
3. Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Решение:
Касательная перпендикулярна радиусу, проведенному в точку касания, значит, треугольник AOB — прямоугольный. Из прямоугольного треугольника AOB по теореме Пифагора найдём AO:
Ответ: 10.
4. На отрезке AB выбрана точка C так, что AC = 75 и BC = 10. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Решение:
Проведём радиус AH в точку касания. Касательная перпендикулярна радиусу, проведенному в точку касания, поэтому треугольник ABН — прямоугольный. Из прямоугольного треугольника ABH по теореме Пифагора найдём BH:
Ответ: 40.
5. Касательные в точках A и B к окружности с центром O пересекаются под углом . Найдите угол ABO. Ответ дайте в градусах.
Решение:
Касательные, проведённые к окружности из одной точки, равны, поэтому AC=BC и треугольник ABC — равнобедренный.
Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними, значит, дуга AB равна . Угол AOB — центральный, он равен дуге, на которую опирается, то есть
. Треугольник AOB равнобедренный,
Ответ: 36.
6. Из точки A проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен , а расстояние от точки A до точки O равно 8.
Решение:
Проведём радиусы OB и OC в точки касания. Треугольники AOB и AOC — прямоугольные. Эти треугольники равны по катету и гипотенузе.
OB — OC как радиусы окружности, гипотенуза общая. Значит,
Из треугольника AOB найдём OB, то есть радиус окружности.
Ответ: 4.
7. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 2, AC = 8. Найдите AK.
Решение:
По теореме о секущей и касательной,
Ответ: 4.
8. На окружности отмечены точки A и B так, что меньшая дуга AB равна . Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Решение:
Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними.
Ответ: 36.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Касательная к окружности» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.01.2023

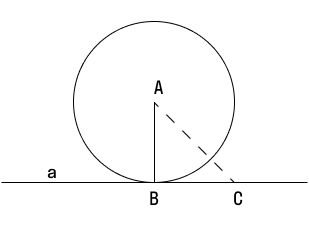
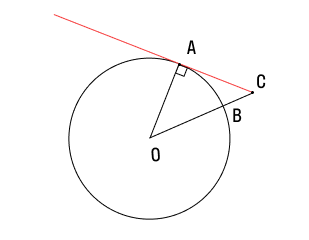
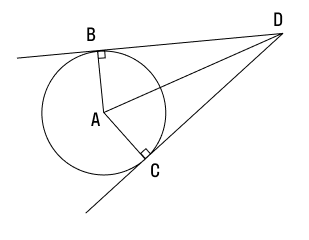
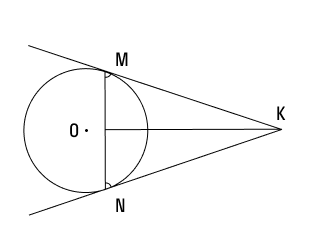
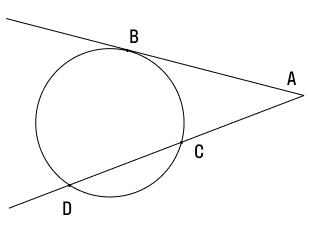
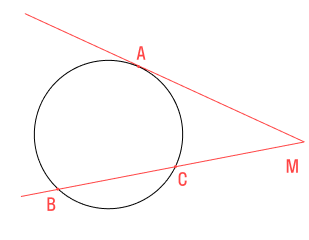
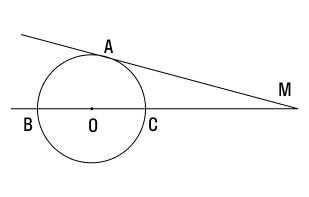































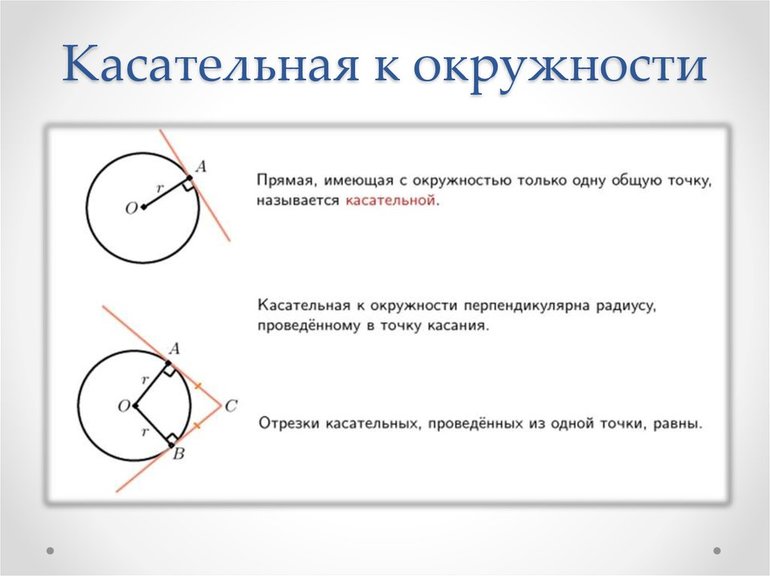
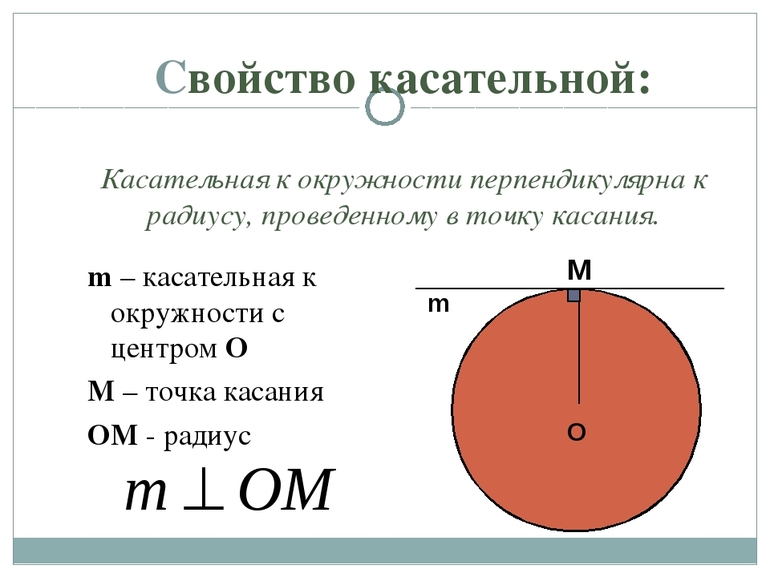

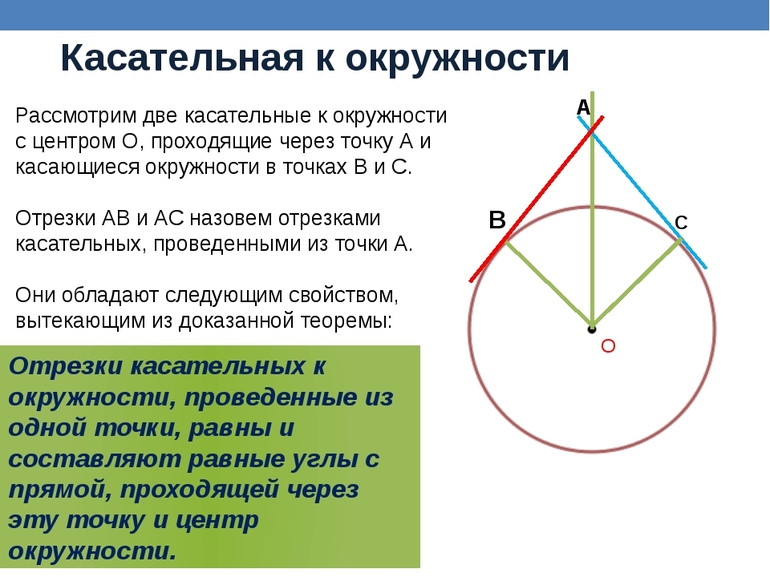

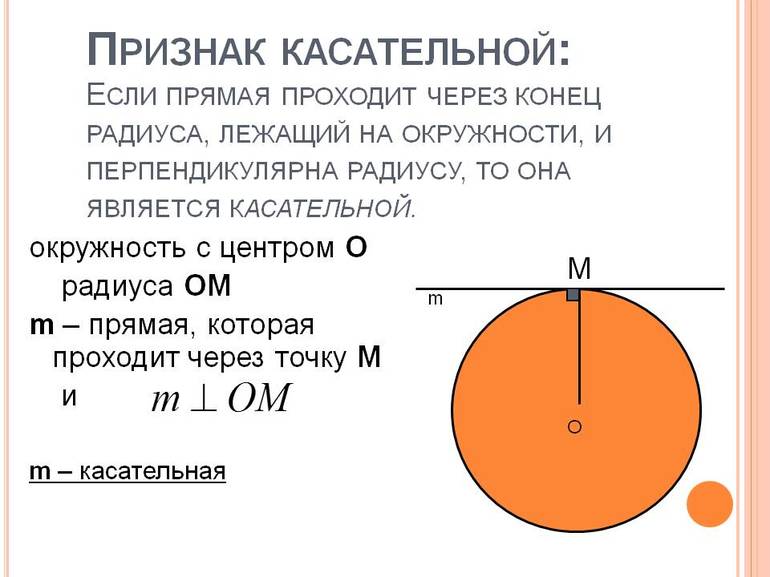

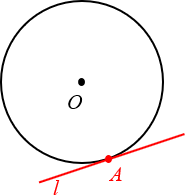
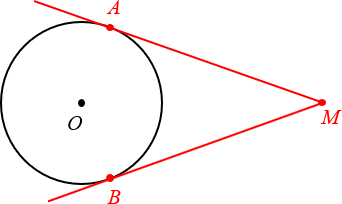
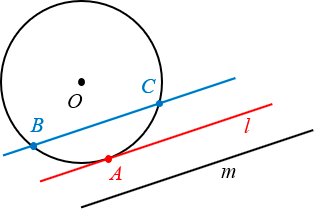
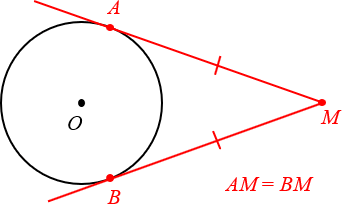
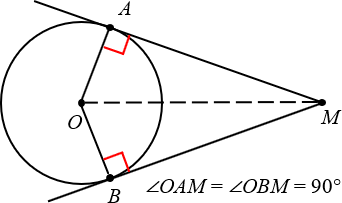
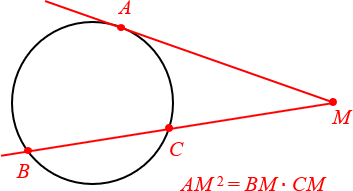
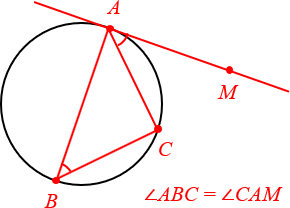


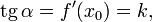
 обозначает тангенс, а
обозначает тангенс, а  — коэффициент наклона касательной. Производная в точке
— коэффициент наклона касательной. Производная в точке 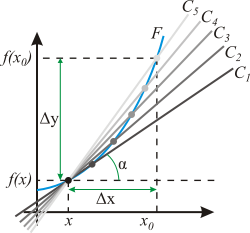
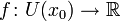 и
и 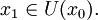 Тогда прямая линия, проходящая через точки
Тогда прямая линия, проходящая через точки 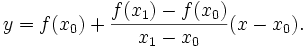
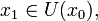 и её угол наклона
и её угол наклона 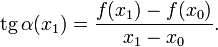
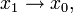 получаем, что существует предел
получаем, что существует предел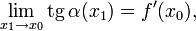

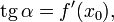 задаётся уравнением касательной:
задаётся уравнением касательной:
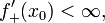 то пра́вой полукаса́тельной к графику функции
то пра́вой полукаса́тельной к графику функции 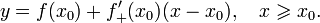
 то ле́вой полукаса́тельной к графику функции
то ле́вой полукаса́тельной к графику функции 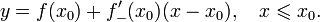
 то правой полукасательной к графику функции
то правой полукасательной к графику функции 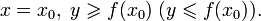
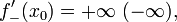 то правой полукасательной к графику функции
то правой полукасательной к графику функции