Со времен возникновения различных наук и математических расчетов ученые начали использовать множество символов и сокращений. Это вполне оправданное решение, ведь длинные формулы, записанные при помощи слов, отнимали бы много времени. По какому принципу выбираются эти обозначения, в частности буквы, указывающие на скорость и расстояние?
Как обозначают физические величины и понятия?
В физике существует общепринятый список обозначений. Он включает латинские и греческие буквы, кириллицу (редко), специальные символы, надстрочные и подстрочные знаки, скобки и др. В качестве самостоятельной науки физика зародилась в 17-м веке во время научной революции, но многие идеи, физические воззрения появились еще в античный период. Отсюда и использование латыни, греческого языка.
Количество физических величин довольно большое – букв в алфавитах недостаточно для обозначения их всех. Поэтому одни и те же буквы могут обозначать разные понятия. Важно различать и стиль написания.
Например, латинские символы обычно пишутся курсивом, греческие – обыкновенным прямым начертанием. Строчными буквами обозначают интенсивные величины (не зависят от размеров системы, например, температура), заглавными – экстенсивные.
Интересный факт: среди всех латинских букв для обозначения понятий из области физики реже всего встречается буква о.
Ввиду исторических причин множество обозначений с использованием латинских букв – это сокращения слов, которые указывают на данные понятия. Чаще всего это латинские, английские, немецкие и французские слова. Во избежание путаницы почти не используются греческие заглавные буквы, если они похожи на латинские по манере написания.
Почему в физике расстояние обозначается буквой s?
Расстояние в физике измеряется единицами длины (метр в международной системе единиц) и имеет два значения:
- степень удаленности объектов друг от друга;
- длина пути, которую прошел объект.
Расстояние – один из тех случаев, когда обозначающая буква является первой в слове-определении. Некоторые источники по-разному объясняют происхождение буквы s:
- От английского слова «space», которое означает расстояние, пространство, площадь.
- От латинского «spatium» – пространство между двумя предметами, протяжение в длину и ширину.
Фактически оба варианта являются правильными. Согласно этимологии слова «space», оно вошло в употребление в 1300-х годах и происходит от французского «espace», а оно, в свою очередь, от латинского «spatium». В значении космического пространства «space» начало употребляться лишь с конца 17-го века, после того как появилось в художественном произведении Джона Мильтона.
Почему в физике скорость обозначается буквой v?
Для обозначения скорости в физике используют строчную букву v тоже не случайно. Это первая буква в латинском слове «velocitas», французском «vitesse» и английском «velocity». Все они означают скорость, быстроту, стремительность.
Возникает другой вопрос: почему именно «velocity» стало определением скорости, а не другие английские слова с похожим значением, например, «speed»? Дело в том, что в физике скорость является векторной величиной, которая отображает быстроту и направление перемещения объекта относительно заданной системы отсчета.
Слово «speed» указывает на скалярную скорость – величину, которая не зависит от системы координат. Например, скорость света – постоянная величина, поэтому на английском данный термин будет выглядеть как «the speed of light».
Кроме того, скорость и расстояние – взаимосвязанные величины наряду со временем. Эта связь в физике выражается формулой. Зная две величины, можно рассчитать и третью. Использование одинаковых букв нецелесообразно.
Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Distance is a numerical or occasionally qualitative measurement of how far apart objects or points are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. «two counties over»). Since spatial cognition is a rich source of conceptual metaphors in human thought,[1] the term is also frequently used metaphorically to mean a measurement of the amount of difference between two similar objects (such as statistical distance between probability distributions or edit distance between strings of text) or a degree of separation (as exemplified by distance between people in a social network). Most such notions of distance, both physical and metaphorical, are formalized in mathematics using the notion of a metric space.
In the social sciences, distance can refer to a qualitative measurement of separation, such as social distance or psychological distance.
Distances in physics and geometry[edit]
The distance between physical locations can be defined in different ways in different contexts.
Straight-line or Euclidean distance[edit]
The distance between two points in physical space is the length of a straight line between them, which is the shortest possible path. This is the usual meaning of distance in classical physics, including Newtonian mechanics.
Straight-line distance is formalized mathematically as the Euclidean distance in two- and three-dimensional space. In Euclidean geometry, the distance between two points A and B is often denoted 
Similarly, given points (x1, y1, z1) and (x2, y2, z2) in three-dimensional space, the distance between them is:[2]
This idea generalizes to higher-dimensional Euclidean spaces.
Measurement[edit]
There are many ways of measuring straight-line distances. For example, it can be done directly using a ruler, or indirectly with a radar (for long distances) or interferometry (for very short distances). The cosmic distance ladder is a set of ways of measuring extremely long distances.
Shortest-path distance on a curved surface[edit]
Airline routes between Los Angeles and Tokyo approximately follow a direct great circle route (top), but use the jet stream (bottom) when heading eastwards. The shortest route appears as a curve rather than a straight line because the map projection does not scale all distances equally compared to the real spherical surface of the Earth.
The straight-line distance between two points on the surface of the Earth is not very useful for most purposes, since we cannot tunnel straight through the Earth’s mantle. Instead, one typically measures the shortest path along the surface of the Earth, as the crow flies. This is approximated mathematically by the great-circle distance on a sphere.
More generally, the shortest path between two points along a curved surface is known as a geodesic. The arc length of geodesics gives a way of measuring distance from the perspective of an ant or other flightless creature living on that surface.
Effects of relativity[edit]
In the theory of relativity, because of phenomena such as length contraction and the relativity of simultaneity, distances between objects depend on a choice of inertial frame of reference. On galactic and larger scales, the measurement of distance is also affected by the expansion of the universe. In practice, a number of distance measures are used in cosmology to quantify such distances.
Other spatial distances[edit]
Unusual definitions of distance can be helpful to model certain physical situations, but are also used in theoretical mathematics:
- In practice, one is often interested in the travel distance between two points along roads, rather than as the crow flies. In a grid plan, the travel distance between street corners is given by the Manhattan distance: the number of east–west and north–south blocks one must traverse to get between those two points.
- Chessboard distance, formalized as Chebyshev distance, is the minimum number of moves a king must make on a chessboard in order to travel between two squares.
Metaphorical distances[edit]
Many abstract notions of distance used in mathematics, science and engineering represent a degree of difference or separation between similar objects. This page gives a few examples.
Statistical distances[edit]
In statistics and information geometry, statistical distances measure the degree of difference between two probability distributions. There are many kinds of statistical distances, typically formalized as divergences; these allow a set of probability distributions to be understood as a geometrical object called a statistical manifold. The most elementary is the squared Euclidean distance, which is minimized by the least squares method; this is the most basic Bregman divergence. The most important in information theory is the relative entropy (Kullback–Leibler divergence), which allows one to analogously study maximum likelihood estimation geometrically; this is an example of both an f-divergence and a Bregman divergence (and in fact the only example which is both). Statistical manifolds corresponding to Bregman divergences are flat manifolds in the corresponding geometry, allowing an analog of the Pythagorean theorem (which holds for squared Euclidean distance) to be used for linear inverse problems in inference by optimization theory.
Other important statistical distances include the Mahalanobis distance and the energy distance.
Edit distances[edit]
In computer science, an edit distance or string metric between two strings measures how different they are. For example, the words «dog» and «dot», which differ by just one letter, are closer than «dog» and «cat», which have no letters in common. This idea is used in spell checkers and in coding theory, and is mathematically formalized in a number of different ways, including Levenshtein distance, Hamming distance, Lee distance, and Jaro–Winkler distance.
Distance in graph theory[edit]
In a graph, the distance between two vertices is measured by the length of the shortest edge path between them. For example, if the graph represents a social network, then the idea of six degrees of separation can be interpreted mathematically as saying that the distance between any two vertices is at most six. Similarly, the Erdős number and the Bacon number—the number of collaborative relationships away a person is from prolific mathematician Paul Erdős and actor Kevin Bacon, respectively—are distances in the graphs whose edges represent mathematical or artistic collaborations.
[edit]
In psychology, human geography, and the social sciences, distance is often theorized not as an objective numerical measurement, but as a qualitative description of a subjective experience.[4] For example, psychological distance is «the different ways in which an object might be removed from» the self along dimensions such as «time, space, social distance, and hypotheticality».[5] In sociology, social distance describes the separation between individuals or social groups in society along dimensions such as social class, race/ethnicity, gender or sexuality.
Mathematical formalization[edit]
Most of the notions of distance between two points or objects described above are examples of the mathematical idea of a metric. A metric or distance function is a function d which takes pairs of points or objects to real numbers and satisfies the following rules:
- The distance between an object and itself is always zero.
- The distance between distinct objects is always positive.
- Distance is symmetric: the distance from x to y is always the same as the distance from y to x.
- Distance satisfies the triangle inequality: if x, y, and z are three objects, then
This condition can be described informally as «intermediate stops can’t speed you up.»
As an exception, many of the divergences used in statistics are not metrics.
Distance between sets[edit]
The distances between these three sets do not satisfy the triangle inequality:
There are multiple ways of measuring the physical distance between objects that consist of more than one point:
- One may measure the distance between representative points such as the center of mass; this is used for astronomical distances such as the Earth–Moon distance.
- One may measure the distance between the closest points of the two objects; in this sense, the altitude of an airplane or spacecraft is its distance from the Earth. The same sense of distance is used in Euclidean geometry to define distance from a point to a line, distance from a point to a plane, or, more generally, perpendicular distance between affine subspaces.
- Even more generally, this idea can be used to define the distance between two subsets of a metric space. The distance between sets A and B is the infimum of the distances between any two of their respective points:
This does not define a metric on the set of such subsets: the distance between overlapping sets is zero, and this distance does not satisfy the triangle inequality for any metric space with two or more points (consider the triple of sets consisting of two distinct singletons and their union).
- The Hausdorff distance between two subsets of a metric space can be thought of as measuring how far they are from perfectly overlapping. Somewhat more precisely, the Hausdorff distance between A and B is either the distance from A to the farthest point of B, or the distance from B to the farthest point of A, whichever is larger. (Here «farthest point» must be interpreted as a supremum.) The Hausdorff distance defines a metric on the set of compact subsets of a metric space.
[edit]
Further information: Length
The word distance is also used for related concepts that are not encompassed by the description «a numerical measurement of how far apart points or objects are».
Distance travelled[edit]
The distance travelled by an object is the length of a specific path travelled between two points,[6] such as the distance walked while navigating a maze. This can even be a closed distance along a closed curve which starts and ends at the same point, such as a ball thrown straight up, or the Earth when it completes one orbit. This is formalized mathematically as the arc length of the curve.
The distance travelled may also be signed: a «forward» distance is positive and a «backward» distance is negative.
Circular distance is the distance traveled by a point on the circumference of a wheel, which can be useful to consider when designing vehicles or mechanical gears (see also odometry). The circumference of the wheel is 2π × radius; if the radius is 1, each revolution of the wheel causes a vehicle to travel 2π radians.
Displacement and directed distance[edit]
Distance along a path compared with displacement. The Euclidean distance is the length of the displacement vector.
The displacement in classical physics measures the change in position of an object during an interval of time. While distance is a scalar quantity, or a magnitude, displacement is a vector quantity with both magnitude and direction. In general, the vector measuring the difference between two locations (the relative position) is sometimes called the directed distance.[7] For example, the directed distance from the New York City Main Library flag pole to the Statue of Liberty flag pole has:
- A starting point: library flag pole
- An ending point: statue flag pole
- A direction: -38°
- A distance: 8.72 km
Signed distance[edit]
In mathematics and its applications, the signed distance function (or oriented distance function) is the orthogonal distance of a given point x to the boundary of a set Ω in a metric space, with the sign determined by whether or not x is in the interior of Ω. The function has positive values at points x inside Ω, it decreases in value as x approaches the boundary of Ω where the signed distance function is zero, and it takes negative values outside of Ω.[8] However, the alternative convention is also sometimes taken instead (i.e., negative inside Ω and positive outside).[9]
See also[edit]
Wikiquote has quotations related to Distance.
- Absolute difference
- Astronomical system of units
- Color difference
- Closeness (mathematics)
- Distance geometry problem
- Dijkstra’s algorithm
- Distance matrix
- Distance set
- Engineering tolerance
- Multiplicative distance
- Optical path length
- Orders of magnitude (length)
- Proper length
- Proxemics – physical distance between people
- Signed distance function
- Similarity measure
- Social distancing
- Vertical distance
Library support[edit]
- Python (programming language)
- Interspace -A package for finding the distance between two vectors, numbers and strings.
- SciPy -Distance computations (
scipy.spatial.distance)
- Julia (programming language)
- Julia Statistics Distance -A Julia package for evaluating distances (metrics) between vectors.
References[edit]
- ^ Schnall, Simone (2014). «Are there basic metaphors?». The power of metaphor: Examining its influence on social life. American Psychological Association. pp. 225–247. doi:10.1037/14278-010.
- ^ a b Weisstein, Eric W. «Distance». mathworld.wolfram.com. Retrieved 2020-09-01.
- ^ «Distance Between 2 Points». www.mathsisfun.com. Retrieved 2020-09-01.
- ^ «SOCIAL DISTANCES». www.hawaii.edu. Retrieved 2020-07-20.
- ^ Trope Y, Liberman N (April 2010). «Construal-level theory of psychological distance». Psychological Review. 117 (2): 440–63. doi:10.1037/a0018963. PMC 3152826. PMID 20438233.
- ^ «What is displacement? (article)». Khan Academy. Retrieved 2020-07-20.
- ^ «The Directed Distance» (PDF). Information and Telecommunication Technology Center. University of Kansas. Archived from the original (PDF) on 10 November 2016. Retrieved 18 September 2018.
- ^ Chan, T.; Zhu, W. (2005). Level set based shape prior segmentation. IEEE Computer Society Conference on Computer Vision and Pattern Recognition. doi:10.1109/CVPR.2005.212.
- ^ Malladi, R.; Sethian, J.A.; Vemuri, B.C. (1995). «Shape modeling with front propagation: a level set approach». IEEE Transactions on Pattern Analysis and Machine Intelligence. 17 (2): 158–175. CiteSeerX 10.1.1.33.2443. doi:10.1109/34.368173.
Bibliography[edit]
- Deza E, Deza M (2006). Dictionary of Distances. Elsevier. ISBN 0-444-52087-2.
Distance is a numerical or occasionally qualitative measurement of how far apart objects or points are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. «two counties over»). Since spatial cognition is a rich source of conceptual metaphors in human thought,[1] the term is also frequently used metaphorically to mean a measurement of the amount of difference between two similar objects (such as statistical distance between probability distributions or edit distance between strings of text) or a degree of separation (as exemplified by distance between people in a social network). Most such notions of distance, both physical and metaphorical, are formalized in mathematics using the notion of a metric space.
In the social sciences, distance can refer to a qualitative measurement of separation, such as social distance or psychological distance.
Distances in physics and geometry[edit]
The distance between physical locations can be defined in different ways in different contexts.
Straight-line or Euclidean distance[edit]
The distance between two points in physical space is the length of a straight line between them, which is the shortest possible path. This is the usual meaning of distance in classical physics, including Newtonian mechanics.
Straight-line distance is formalized mathematically as the Euclidean distance in two- and three-dimensional space. In Euclidean geometry, the distance between two points A and B is often denoted 
Similarly, given points (x1, y1, z1) and (x2, y2, z2) in three-dimensional space, the distance between them is:[2]
This idea generalizes to higher-dimensional Euclidean spaces.
Measurement[edit]
There are many ways of measuring straight-line distances. For example, it can be done directly using a ruler, or indirectly with a radar (for long distances) or interferometry (for very short distances). The cosmic distance ladder is a set of ways of measuring extremely long distances.
Shortest-path distance on a curved surface[edit]
Airline routes between Los Angeles and Tokyo approximately follow a direct great circle route (top), but use the jet stream (bottom) when heading eastwards. The shortest route appears as a curve rather than a straight line because the map projection does not scale all distances equally compared to the real spherical surface of the Earth.
The straight-line distance between two points on the surface of the Earth is not very useful for most purposes, since we cannot tunnel straight through the Earth’s mantle. Instead, one typically measures the shortest path along the surface of the Earth, as the crow flies. This is approximated mathematically by the great-circle distance on a sphere.
More generally, the shortest path between two points along a curved surface is known as a geodesic. The arc length of geodesics gives a way of measuring distance from the perspective of an ant or other flightless creature living on that surface.
Effects of relativity[edit]
In the theory of relativity, because of phenomena such as length contraction and the relativity of simultaneity, distances between objects depend on a choice of inertial frame of reference. On galactic and larger scales, the measurement of distance is also affected by the expansion of the universe. In practice, a number of distance measures are used in cosmology to quantify such distances.
Other spatial distances[edit]
Unusual definitions of distance can be helpful to model certain physical situations, but are also used in theoretical mathematics:
- In practice, one is often interested in the travel distance between two points along roads, rather than as the crow flies. In a grid plan, the travel distance between street corners is given by the Manhattan distance: the number of east–west and north–south blocks one must traverse to get between those two points.
- Chessboard distance, formalized as Chebyshev distance, is the minimum number of moves a king must make on a chessboard in order to travel between two squares.
Metaphorical distances[edit]
Many abstract notions of distance used in mathematics, science and engineering represent a degree of difference or separation between similar objects. This page gives a few examples.
Statistical distances[edit]
In statistics and information geometry, statistical distances measure the degree of difference between two probability distributions. There are many kinds of statistical distances, typically formalized as divergences; these allow a set of probability distributions to be understood as a geometrical object called a statistical manifold. The most elementary is the squared Euclidean distance, which is minimized by the least squares method; this is the most basic Bregman divergence. The most important in information theory is the relative entropy (Kullback–Leibler divergence), which allows one to analogously study maximum likelihood estimation geometrically; this is an example of both an f-divergence and a Bregman divergence (and in fact the only example which is both). Statistical manifolds corresponding to Bregman divergences are flat manifolds in the corresponding geometry, allowing an analog of the Pythagorean theorem (which holds for squared Euclidean distance) to be used for linear inverse problems in inference by optimization theory.
Other important statistical distances include the Mahalanobis distance and the energy distance.
Edit distances[edit]
In computer science, an edit distance or string metric between two strings measures how different they are. For example, the words «dog» and «dot», which differ by just one letter, are closer than «dog» and «cat», which have no letters in common. This idea is used in spell checkers and in coding theory, and is mathematically formalized in a number of different ways, including Levenshtein distance, Hamming distance, Lee distance, and Jaro–Winkler distance.
Distance in graph theory[edit]
In a graph, the distance between two vertices is measured by the length of the shortest edge path between them. For example, if the graph represents a social network, then the idea of six degrees of separation can be interpreted mathematically as saying that the distance between any two vertices is at most six. Similarly, the Erdős number and the Bacon number—the number of collaborative relationships away a person is from prolific mathematician Paul Erdős and actor Kevin Bacon, respectively—are distances in the graphs whose edges represent mathematical or artistic collaborations.
[edit]
In psychology, human geography, and the social sciences, distance is often theorized not as an objective numerical measurement, but as a qualitative description of a subjective experience.[4] For example, psychological distance is «the different ways in which an object might be removed from» the self along dimensions such as «time, space, social distance, and hypotheticality».[5] In sociology, social distance describes the separation between individuals or social groups in society along dimensions such as social class, race/ethnicity, gender or sexuality.
Mathematical formalization[edit]
Most of the notions of distance between two points or objects described above are examples of the mathematical idea of a metric. A metric or distance function is a function d which takes pairs of points or objects to real numbers and satisfies the following rules:
- The distance between an object and itself is always zero.
- The distance between distinct objects is always positive.
- Distance is symmetric: the distance from x to y is always the same as the distance from y to x.
- Distance satisfies the triangle inequality: if x, y, and z are three objects, then
This condition can be described informally as «intermediate stops can’t speed you up.»
As an exception, many of the divergences used in statistics are not metrics.
Distance between sets[edit]
The distances between these three sets do not satisfy the triangle inequality:
There are multiple ways of measuring the physical distance between objects that consist of more than one point:
- One may measure the distance between representative points such as the center of mass; this is used for astronomical distances such as the Earth–Moon distance.
- One may measure the distance between the closest points of the two objects; in this sense, the altitude of an airplane or spacecraft is its distance from the Earth. The same sense of distance is used in Euclidean geometry to define distance from a point to a line, distance from a point to a plane, or, more generally, perpendicular distance between affine subspaces.
- Even more generally, this idea can be used to define the distance between two subsets of a metric space. The distance between sets A and B is the infimum of the distances between any two of their respective points:
This does not define a metric on the set of such subsets: the distance between overlapping sets is zero, and this distance does not satisfy the triangle inequality for any metric space with two or more points (consider the triple of sets consisting of two distinct singletons and their union).
- The Hausdorff distance between two subsets of a metric space can be thought of as measuring how far they are from perfectly overlapping. Somewhat more precisely, the Hausdorff distance between A and B is either the distance from A to the farthest point of B, or the distance from B to the farthest point of A, whichever is larger. (Here «farthest point» must be interpreted as a supremum.) The Hausdorff distance defines a metric on the set of compact subsets of a metric space.
[edit]
Further information: Length
The word distance is also used for related concepts that are not encompassed by the description «a numerical measurement of how far apart points or objects are».
Distance travelled[edit]
The distance travelled by an object is the length of a specific path travelled between two points,[6] such as the distance walked while navigating a maze. This can even be a closed distance along a closed curve which starts and ends at the same point, such as a ball thrown straight up, or the Earth when it completes one orbit. This is formalized mathematically as the arc length of the curve.
The distance travelled may also be signed: a «forward» distance is positive and a «backward» distance is negative.
Circular distance is the distance traveled by a point on the circumference of a wheel, which can be useful to consider when designing vehicles or mechanical gears (see also odometry). The circumference of the wheel is 2π × radius; if the radius is 1, each revolution of the wheel causes a vehicle to travel 2π radians.
Displacement and directed distance[edit]
Distance along a path compared with displacement. The Euclidean distance is the length of the displacement vector.
The displacement in classical physics measures the change in position of an object during an interval of time. While distance is a scalar quantity, or a magnitude, displacement is a vector quantity with both magnitude and direction. In general, the vector measuring the difference between two locations (the relative position) is sometimes called the directed distance.[7] For example, the directed distance from the New York City Main Library flag pole to the Statue of Liberty flag pole has:
- A starting point: library flag pole
- An ending point: statue flag pole
- A direction: -38°
- A distance: 8.72 km
Signed distance[edit]
In mathematics and its applications, the signed distance function (or oriented distance function) is the orthogonal distance of a given point x to the boundary of a set Ω in a metric space, with the sign determined by whether or not x is in the interior of Ω. The function has positive values at points x inside Ω, it decreases in value as x approaches the boundary of Ω where the signed distance function is zero, and it takes negative values outside of Ω.[8] However, the alternative convention is also sometimes taken instead (i.e., negative inside Ω and positive outside).[9]
See also[edit]
Wikiquote has quotations related to Distance.
- Absolute difference
- Astronomical system of units
- Color difference
- Closeness (mathematics)
- Distance geometry problem
- Dijkstra’s algorithm
- Distance matrix
- Distance set
- Engineering tolerance
- Multiplicative distance
- Optical path length
- Orders of magnitude (length)
- Proper length
- Proxemics – physical distance between people
- Signed distance function
- Similarity measure
- Social distancing
- Vertical distance
Library support[edit]
- Python (programming language)
- Interspace -A package for finding the distance between two vectors, numbers and strings.
- SciPy -Distance computations (
scipy.spatial.distance)
- Julia (programming language)
- Julia Statistics Distance -A Julia package for evaluating distances (metrics) between vectors.
References[edit]
- ^ Schnall, Simone (2014). «Are there basic metaphors?». The power of metaphor: Examining its influence on social life. American Psychological Association. pp. 225–247. doi:10.1037/14278-010.
- ^ a b Weisstein, Eric W. «Distance». mathworld.wolfram.com. Retrieved 2020-09-01.
- ^ «Distance Between 2 Points». www.mathsisfun.com. Retrieved 2020-09-01.
- ^ «SOCIAL DISTANCES». www.hawaii.edu. Retrieved 2020-07-20.
- ^ Trope Y, Liberman N (April 2010). «Construal-level theory of psychological distance». Psychological Review. 117 (2): 440–63. doi:10.1037/a0018963. PMC 3152826. PMID 20438233.
- ^ «What is displacement? (article)». Khan Academy. Retrieved 2020-07-20.
- ^ «The Directed Distance» (PDF). Information and Telecommunication Technology Center. University of Kansas. Archived from the original (PDF) on 10 November 2016. Retrieved 18 September 2018.
- ^ Chan, T.; Zhu, W. (2005). Level set based shape prior segmentation. IEEE Computer Society Conference on Computer Vision and Pattern Recognition. doi:10.1109/CVPR.2005.212.
- ^ Malladi, R.; Sethian, J.A.; Vemuri, B.C. (1995). «Shape modeling with front propagation: a level set approach». IEEE Transactions on Pattern Analysis and Machine Intelligence. 17 (2): 158–175. CiteSeerX 10.1.1.33.2443. doi:10.1109/34.368173.
Bibliography[edit]
- Deza E, Deza M (2006). Dictionary of Distances. Elsevier. ISBN 0-444-52087-2.
Среди прочих обозначений наиболее часто школьников интересует вопрос о том, как в математике обозначается скорость, время, расстояние. Связано это с тем, что обозначения этих величин (особенно — скорости) в учебниках по математике и физике можно увидеть различные: с чертой над буквой v (читается: [вэ]), со стрелкой над буквой v, а также буквы v, выделенные курсивом или жирным шрифтом.
Скорость в математике обозначается буквой v, но её написание принято различным для рукописного и печатного текста.
В рукописном тексте скорость движения обычно обозначается строчной (т.е. маленькой) прописной (т.е. не печатной, как в тексте из газеты, а написанной от руки так, как если бы писали письмо) буквой v. В учебниках по математике (т.е. в печатном тексте) обычно скорость движения обозначается печатной буквой v, прямой или выделенной курсивом. Такое обозначение принимается практически во всех задачах по математике, исключение составляют лишь задачи, иллюстрирующие тему «Векторы» (в этом случае обозначение принимается таким же, как и в физике).
В физике (а точнее – в её разделе «механика») обозначение скорости зависит от того, нужно ли в данной задаче учитывать тот факт, что скорость – величина векторная. Там, где учитывать это не нужно, скорость обозначается строчной буквой v (печатной или прописной, так же, как и в математике). Если же необходимо учитывать то, что скорость характеризуется не только модулем (т.е. величиной), но и направлением, скорость изображается либо прописной буквой v с направленной слева направо стрелкой над этой буквой, либо той же прописной буквой v с горизонтальной чертой над этой буквой. В печатном тексте в этом случае обычно скорость обозначают либо печатной строчной буквой v со стрелкой или чертой над буквой, либо печатной буквой v, выделенной жирным шрифтом (т.е. так: v).
Буквой v обозначают скорость движения тел. Для обозначения скорости света и скорости звука принята другая, отличная от обозначения скорости движения тел, буква. Скорость света обозначается буквой «с» (скорость света в вакууме составляет с = 2,9979х108 м/с = 2,9979х105 км/с). Скорость звука так же обозначается буквой с (читается: [цэ]).
Ускорение обозначается буквой а (исключение составляет лишь ускорение свободного падения, эта величина обозначается буквой g (читается [жэ]), g = 9,81 м/с2). Если необходимо подчеркнуть, что эта величина – векторная (например, это часто требуется в физике), то над буквой «а» изображается либо горизонтальная черта, либо горизонтальная стрелка (так же, как и при обозначении скорости). В печатном тексте для обозначения ускорения как векторной величины может использоваться и буква «а», выделенная жирным шрифтом.
Если при решении задачи по физике или математике необходимо обозначить время, то это пишется буквой так: t (читается: [тэ]), а если расстояние — пишется буквой так: s (читается: [эс]). Для обозначения пути обычно используется строчная (маленькая) буква [эль], т.е. l, реже — заглавная (большая) буква [эль], т.е. L. Чтобы обозначение пути «l» не было похоже на «единицу», эту букву пишут курсивом, т.е. с наклоном.
Вообще, вопросы «как в математике пишется скорость», «как в математике пишется время», «как в математике пишется расстояние» некорректны. Лучше формулировать такой вопрос, употребляя не слово «пишется», а слово «обозначается».
Источники:
- Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике для инженеров и студентов вузов
- Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра/ Под ред. П.Ф. Фильчакова
- Каплан И.А. Практические занятия по высшей математике
Дополнительная информация:
- ru.wikipedia.org – Список обозначений в физике
- azbyka.kz — Урок математики «Скорость, время, расстояние»
В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.
Расстояние
Расстояние мы уже изучали в уроке единицы измерения. Говоря простым языком, расстояние это длина от одного пункта до другого. (Пример: расстояние от дома до школы 2 километра).
Имея дело с большими расстояниями, в основном они будут измеряться в метрах и километрах. Расстояние обозначается латинской буквой S. Можно обозначить и другой буквой, но буква S общепринята.
Скорость
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Предположим, что двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал бóльшее расстояние. Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Давайте найдём скорость первого школьника. Для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 м : 25 с = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит скорость измеряется в метрах в секунду (м/с)
100м : 25с = 4 (м/с)
Итак, скорость движения первого школьника составляет 4 метра в секунду (м/с).
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 м : 50 c = 2 (м/с)
Значит скорость движения второго школьника составляет 2 метра в секунду (м/с).
Скорость движения первого школьника — 4 (м/с)
Скорость движения второго школьника — 2 (м/с)
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.
Время
Иногда возникает ситуация, когда требуется узнать за какое время тело преодолеет то или иное расстояние.
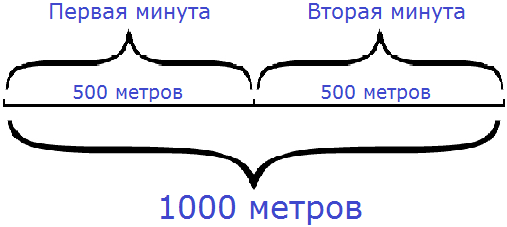
Например, от дома до спортивной секции 1000 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 500 метров в минуту (500м/мин). За какое время мы доедем до спортивной секции?
Если за одну минуту мы будем проезжать 500 метров, то сколько таких минут с пятью ста метрами будет в 1000 метрах?
Очевидно, что надо разделить 1000 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 500 метров. Тогда мы получим время, за которое доедем до спортивной секции:
1000 : 500 = 2 (мин)
Время движения обозначается маленькой латинской буквой t.
Взаимосвязь скорости, времени, расстояния
Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
s = v × t
Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Очевидно, что умножив 50 метров на 10, мы определим расстояние от дома до магазина:
v = 50 (м/мин)
t = 10 минут
s = v × t = 50 × 10 = 500 (метров до магазина)
Если известно время и расстояние, то можно найти скорость:
v = s : t
Например, расстояние от дома до школы 900 метров. Школьник дошел до этой школы за 10 минут. Какова была его скорость?
Скорость движения школьника это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот, нужно разделить расстояние на время движения школьника:
s = 900 метров
t = 10 минут
v = s : t = 900 : 10 = 90 (м/мин)
Если известна скорость и расстояние, то можно найти время:
t = s : v
Например, от дома до спортивной секции 500 метров. Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до спортивной секции:
s = 500 метров
v = 100 (м/мин)
t = s : v = 500 : 100 = 5 (минут до спортивной секции)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
- Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути
Чтобы найти расстояние, нужно умножить скорость на время движения:
s = v × t
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
- Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени
Чтобы найти время, нужно разделить расстояние на скорость:
t = s : v
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Как рассуждаем:
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:
v = 50 м/мин
t = 15 мин
s = v × t = 50 × 15 = 750 (м)
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Как рассуждаем:
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 : 25 = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
100 м : 25 с = 4 м/с
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 : 50 = 2
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Как рассуждаем:
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
s = 500 м
v = 100 м/мин
t = s : v = 500 : 100 = 5 (мин)
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
В физике расстояние и перемещение используются для обозначения длины между двумя точками. Однако эти понятия не одно и то же.
Расстояние
Это длина фактического пути между двумя точками.
Перемещение
Это длина кратчайшего пути между двумя точками.
Таким образом, расстояние говорит нам, сколько пути пройдено телом, во время движения, а перемещение дает нам представление о том, как далеко тело находится от своей начальной точки, и в каком направлении. Разница между расстоянием и перемещением часто путается или приравнивается, однако для решения физических задач, понимание сути этих двух терминов очень важно.
Сравнительная таблица расстояния и перемещения
| Параметры сравнений | Расстояние | Перемещение |
| Определение | Расстояние относится к количеству пространства между двумя точками, измеренного вдоль фактического пути, связывающего их. | Перемещение означает количество пространства между двумя точками, измеренное вдоль минимального пути, связывающего их. |
| Что это значит физически? | Длина всего проспекта, пройденного телом. | Наименьшее расстояние между начальной и конечной точкой. |
| Скаляр или вектор | Скалярная величина | Векторная величина |
| Информация | Дает полную информацию о маршруте, по которому следует тело. | Не дает полной информации о маршруте следования тела. |
| Время | Расстояние никогда не может уменьшиться со временем. | Перемещение может уменьшиться со временем. |
| Величина | Положительная | Положительная, Отрицательная или Ноль |
| Формула | Скорость × Время | Скорость × Время |
Определение перемещения
Перемещение означает изменение положения кого-либо или чего-либо в определенном направлении. Это самая короткая длина, измеренная от исходного положения до конечного положения движущегося тела. Это векторная величина, поэтому она учитывает как величину, так и направление объекта. Величина перемещения относится к линейному расстоянию между двумя точками.
Как правило, измерение перемещения выполняется по прямой линии, хотя его измерение также может быть выполнено по изогнутым траекториям. Кроме того, измерение выполняется с учетом контрольной точки.
Ссылки[ | ]
- Медиафайлы на Викискладе
- Stopudov.info: единицы длины метрические, национальных систем, древних государств;
- Белобров В. А.
Традиционная русская система мер длины. Краткое описание. - Белобров В. А.
Традиционные русские меры длины (книга) - Белобров В. А.
Меры длины Средиземноморья: от Древнего Египта к средневековой Византии (книга) - Белобров В. А.
Система русских саженей: мифы и загадки. - Белобров В. А.
Кто ты, русский аршин? - Белобров В. А.
Из чего сверстаны версты?. - Белобров В. А.
О протяжённости древнерусских дорог. - Белобров В. А.
Роль Петра I в развитии русской системы мер длины
Ключевые различия между расстоянием и перемещением
Следующие пункты объясняют разницу между расстоянием и перемещением:
- Количество пространства между двумя точками, измеренное вдоль фактического пути, соединяющего две точки, называется расстоянием. Количество пространства между двумя точками, измеренное вдоль минимального пути, который их соединяет, называется перемещением.
- Расстояние – это не что иное, как длина всего маршрута, пройденного объектом во время движения. С другой стороны, перемещение – это наименьшее расстояние между начальной и конечной точкой.
- Расстояние дает полную информацию о пути, по которому идет тело. В отличие от этого, перемещение не дает полной информации о пути, пройденном объектом.
- Перемещение уменьшается со временем, тогда как расстояние не уменьшается со временем.
- Значение перемещения может быть положительным, отрицательным или даже нулевым, но значение расстояния всегда положительное.
- Расстояние – это скалярная мера, которая учитывает только величину, то есть нам нужно указать только числовое значение. В отличие от перемещения, которое является векторной мерой и учитывает как величину, так и направление.
- Пройденное расстояние не является уникальным путем, но перемещение между двумя точками является уникальным путем.
Как обозначают физические величины и понятия?
В физике существует общепринятый список обозначений. Он включает латинские и греческие буквы, кириллицу (редко), специальные символы, надстрочные и подстрочные знаки, скобки и др. В качестве самостоятельной науки физика зародилась в 17-м веке во время научной революции, но многие идеи, физические воззрения появились еще в античный период. Отсюда и использование латыни, греческого языка.
Количество физических величин довольно большое – букв в алфавитах недостаточно для обозначения их всех. Поэтому одни и те же буквы могут обозначать разные понятия. Важно различать и стиль написания.
Например, латинские символы обычно пишутся курсивом, греческие – обыкновенным прямым начертанием. Строчными буквами обозначают интенсивные величины (не зависят от размеров системы, например, температура), заглавными – экстенсивные.
Интересный факт: среди всех латинских букв для обозначения понятий из области физики реже всего встречается буква о.
Ввиду исторических причин множество обозначений с использованием латинских букв – это сокращения слов, которые указывают на данные понятия. Чаще всего это латинские, английские, немецкие и французские слова. Во избежание путаницы почти не используются греческие заглавные буквы, если они похожи на латинские по манере написания.
Интересно: Как обрабатывают корпус самолета для снижения сопротивления?
Ход урока
Организационный момент
Психологический настрой
Прозвенел заливистый школьный звонок. Начинается новый урок. Мы готовы считать и задачи решать.
Учитель
: Я улыбнулась вам, и вы улыбнитесь друг другу, и подумайте, как хорошо, что мы сегодня все вместе. Мы спокойны, добры и приветливы. Глубоко вдохните и выдохните. Выдохните вчерашнюю обиду и злость, беспокойство. Забудьте о них. Я желаю вам хорошего настроения.
Сообщение темы и цели урока
Сегодня на уроке мы с вами вспомним о величинах, с которыми познакомились на предыдущих уроках и решали с ними задачи на движение и ставить свои ответы на листах самооценки.
(Ответы учащихся) Верно, это скорость, время, расстояние. Какими латинскими буквами они обозначаются. (s, v, t).
Слайд № 1
Девиз нашего урока: «Один за всех, все за одного»
Работа в парах
На партах карточки с примерами:
Увеличь произведение чисел 805 и 5 на 1025 (5050) Из 10000 вычти частное число 40025 и 5 (1995) Увеличь частное чисел 4025 и 5 в 100 раз (80500) Прибавь к числу 1207 частное чисел 51300 и 9 (6907) Из произведения чисел 480 и 7 вычти число 1406 (1954) Произведение чисел 4070 и 6 уменьши на 4420 (20000) Записать ответы в порядке возрастания (ответ записан на интерактивной доске)
Минутка чистописания
Слайд № 2
2 4 6 8 10 (образец в тетради)
Прочитайте числа. Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Индивидуальная работа по карточкам
(4 ученика решают № 7)
Устная работа с остальными учениками:
В саду растут груши и ивы. На груше росло 69 груш, а на иве на 100 груш больше. Сколько груш росло на иве?
Мама варила одно яйцо 5 минут. Сколько времени будет варить 3 яйца?
Масса 1 мешка сахара 50 кг. Сколько кг в 4 таких мешках?
За 1 с человек делает 2 шага. Сколько шагов он сделает за 5 с.? За 10 с?
Слайд № 3
Физминутка
Слайд № 4
Качу, лечу во весь опор. (Выполняют ходьбу на месте.) Я сам — шофер (Имитируют управление автомобильным рулем.) И сам — мотор. (Круговые движения плечами вперед-назад.) Нажимаю на педаль, (Имитируют нажимание на педаль.) И машина мчится вдаль! (Бег на месте.)
Первичное закрепление
Слайд № 5
Орел летел со скоростью 20 км/ч. За сколько часов он пролетит 80 км?
Cкорость полета космического спутника 8 км/сек. Сколько км он пролетит за 10 сек?
Слайд № 6
Решение задачи № 2
Автобус
S — 90 км 90: 45= 2 часа T — ? V — 45 км/ч
Легковая машина
S — 270 км 270: 90 = 3 часа T — ? V — 90 км/ч
Самостоятельная работа по учебнику
Итог урока
Давайте подведем итог урока
Чем занимались на уроке?
Что запомнили?
Рефлексия
Окрасьте сегодняшний урок (Дети рисуют сердечко своего настроения от урока) Учитель объясняет значении выбранного цвета.
- Красный — радость
- Жёлтый — приятное
- Зелёный — спокойное
- Синий — грустное
- Фиолетовый — тревожный
- Оранжевый — удовлетворение
- Чёрный — неудовлетворение
И на память об уроке солнышко дарит вам частичку своего тепла и хорошего настроения.
Наш закончен урок — Спасибо за внимание, Будем рады новой встрече, Всем Вам до свидания!
Однажды случайный прохожий спросил Эзопа: «Как скоро я доберусь до города?» Эзоп ответил: «Не знаю». Прохожему ничего не оставалось, как только пойти дальше своей дорогой – и тогда Эзоп крикнул ему вслед: «Ты дойдёшь до города к полудню!» Прохожий удивился: «Почему же ты не ответил мне сразу, если знал ответ?» И Эзоп сказал: «Как же я мог сказать это, не зная, как ты ходишь?»
Действительно, о том, что время, расстояние и скорость – величины взаимосвязанные, известно давно. Из этого логически следует, что зная две из них, можно вычислить третью. Формула тоже представляется предельно логичной: если скорость равна, например, 60 км/ч (возьмём для примера разрешённую скорость автомобиля в городе) – т.е. за час он проезжает 60 километров, то для нахождения расстояния, которое он преодолеет за два часа, нам надо всего лишь умножить шестьдесят на два – в результате мы получаем 120 километров.
Представим это в виде формулы. Расстояние в физике принято обозначать латинской буквой S – почему так, с точностью сказать нельзя, это связывают и с немецким словом «Spur», что переводится как «колея» или «след», и с латинскими словами «sulcus» – что значит «борозда» – и «semita», переводимом как «тропинка» или «путь». Яснее происхождение обозначений для других составляющих этой формулы. Время обозначается латинской буквой t – от латинского слова «tempus», которое, собственно и означает – «время» (к нему же восходит музыкальный термин «темп» – хотя в этом можно усмотреть некоторую «путаницу»: темп в музыке – это всё-таки ближе к понятию скорости, чем времени). Время же – латинская буква v – что опять же связано с латынью: «скорость» на этом языке именуется «velocitas».
Итак, формула расстояния выглядит следующим образом: v×t=s
Исходя из этого – и зная правила умножения и деления, разумеется, которые изучают во втором классе, когда и начинают решать такие задачи – мы легко можем найти и другие составляющие. Как мы помним из начальной школы, чтобы вычислить один из множителей, необходимо разделить произведение (т.е. результат умножения) на другой из них. Иными словами, делим расстояние (s) на время (t) – получаем скорость (v), если же нам нужно вычислить время(v) – поступаем наоборот, т.е. делим расстояние на время.
Ничего сложного в таких вычислениях нет – так что с ними с лёгкостью справляются уже второклассники… правда, такая формула предполагает, что объект, с которым мы имеем дело, постоянно движется с одной и той же скоростью (такое движение в физике называется равномерным) – что далеко не всегда имеет место в реальности. Что делать, если скорость движущегося тела изменяется – как бывает, например, когда автомобиль трогается с места?
Тут мы уже имеем дело с более сложной формулой – а именно, с формулой равноускоренного движения, для которого приходится ввести новую величину – ускорение, традиционно обозначаемое латинской буквой a. Чтобы вычислить расстояние при равноускоренном движении (при условии, что тело стартует из состояния покоя), нам придётся умножить ускорение на возведённое в квадрат время, а результат разделить на два.
Остаётся один вопрос – как вычислить ускорение? Для этого надо знать начальную скорость и конечную, соотношение между которыми характеризуется такой формулой:
(v – это конечная скорость, а v0 – начальная). «Вытащить» ускорение из этой формулы – не проблема: из конечной скорости вычитаем начальную и делим результат на время.
Остаётся только добавить, что формулами, характеризующими равноускоренное движение, мы обязаны Г.Галилею, который изучал это явление на примере ускорения при свободном падении.
Как решать задачи на движение? Формула зависимости между скоростью, временем и расстоянием. Задачи и решения.
Содержание
- 1 Единицы измерения расстояния
- 2 Метрическая система
- 3 Британская/американская система
- 4 Старорусская система
- 5 Японская система
- 6 Древнегреческая система
- 7 Типографическая система
- 8 Флотская система
- 9 Единицы, применяемые в астрономии
- 10 Единицы, применяемые в физике
- 11 Единицы, применяемые в технике
- 12 Ссылки
- 13 Примечания
Единицы измерения расстояния
Метрическая система
Единицей измерения расстояния и одной из основных единиц в Международной системе единиц (СИ) является метр. Метр также является единицей измерения расстояния и относится к числу основных единиц в метрических системах МКС, МКСА, МКСК, МКСГ, МСК, МКСЛ, МСС, МКГСС и МТС[1].
В системе СГС единицей измерения расстояния служит сантиметр.
На практике применяются также кратные и дольные единицы метра, образуемые с помощью стандартных приставок СИ:
| Кратные | Дольные | ||||||
| величина | название | обозначение | величина | название | обозначение | ||
| 101 м | декаметр | дам | dam | 10−1 м | дециметр | дм | dm |
| 102 м | гектометр | гм | hm | 10−2 м | сантиметр | см | cm |
| 103 м | километр | км | km | 10−3 м | миллиметр | мм | mm |
| 106 м | мегаметр | Мм | Mm | 10−6 м | микрометр | мкм | µm |
| 109 м | гигаметр | Гм | Gm | 10−9 м | нанометр | нм | nm |
| 1012 м | тераметр | Тм | Tm | 10−12 м | пикометр | пм | pm |
| 1015 м | петаметр | Пм | Pm | 10−15 м | фемтометр | фм | fm |
| 1018 м | эксаметр | Эм | Em | 10−18 м | аттометр | ам | am |
| 1021 м | зеттаметр | Зм | Zm | 10−21 м | зептометр | зм | zm |
| 1024 м | иоттаметр | Им | Ym | 10−24 м | иоктометр | им | ym |
| применять не рекомендуется не применяются или редко применяются на практике |
Британская/американская система
- Лига (лье) = 4,828032 км
- Миля = 1,609344 км
- Фурлонг = 201,16 м
- Чейн = 20,1168 м
- Род = 5,0292 м
- Ярд = 91,44 см
- Инспекционный фут = 1,000002 фута = 30,48006096 см
- Фут = 30,48 см
- Линк = 20,1168 см
- Хэнд = 10,16 см
- Дюйм = 2,54 см
- Линия большая = 0,254 см
- Линия малая = 0,2116 см
- Мил = 0,0254 мм
Старорусская система
- 1 пядь = 17,78 см
- 2 пяди = 1 стопа (35,56 см)
- 3 пяди = 1 локоть (53,34 см)
- 4 пяди = 1 аршин (71,12 см)
- 5 пядей = 1 шаг (88,9 см)
- 6 пядей = 1 мера или полсаженя (106,68 см)
- 7 пядей = 1 лоб (124,46см) (7 пядей во лбу)
- 8 пядей = 1 столбец (142,24 см)
- 9 пядей = 1 посох (160,02 см)
- 10 пядей = 1 витой посох (177,8 см)
- 12 пядей = 1 сажень (213,36 см) (катет)
- 16 пядей = 1 круг (284,48 см)
- 17 пядей = 1 косая сажень (302,26 см) (гипотенуза)
- 1/2 пяди = 1 пясть (8,89 см)
- 1/4 пяди = 1 вершок (4,445 см)
- 1/16 пяди = 1 нокоть (1,11125 см)
- 1/256 пяди (1/16 ноктя) = 1 линия (0,069453 см)
- 1/4096 пяди (1/16 линии) = 1 волос (0,00434 см)
- 1/65536 пяди (1/16 волоса) = 1 волосок (0,00027 см)
- 1 верста = 6000 пядей (1066,8 метров)
- 1 столбовая верста = 1517,41632 метра
- 1 мерная верста = 1000 саженей (2133,6 метра)
- 1 миля = 7 вёрст (7,4676 км)
- Великая сажень ≈ 244,0 см
- Городовая сажень ≈ 284,8 см
- Греческая сажень ≈ 230,4 см позже приравняли аттический стадий = 6 английских футов 1 дюйм = 185,42 см
- Казённая (мерная, трёхаршинная) сажень. В XVI веке сажень была приравнена к 3 аршинам и стала называться казённой, или трёхаршинной (213,36 см)
- Кладочная сажень ≈ 159,7 см
- Косая сажень — расстояние от пальцев ноги до конца пальцев руки, вытянутой над головой по диагонали ≈ 248 см
- Малая сажень — расстояние от поднятой на уровень плеча руки до пола ≈ 142,4 см
- Маховая сажень — расстояние между вытянутыми пальцами раскинутых (размахнутых) рук. В таких маховых саженях, которые легко отсчитывать, выражена, например, высота колокольни Ивана Великого в Кремле. Эта наиболее древняя мера начиная с XVI века перешла в разряд неофициальных, бытовых. = 2,5 аршина = 152—177,8 см
- Морская сажень = 6 английским футам = 182,88 см
- Народная сажень ≈ 176,0 см
- Простая сажень ≈ 150,8 см
- Сажень без чети — наибольшее расстояние между подошвой левой ноги и концом большого пальца поднятой вверх правой руки ≈ 197,2 см
- Трубная сажень — мерили только длину труб на соляных промыслах ≈ 187 см
- Царская сажень ≈ 197,4 см
- Церковная сажень ≈ 186,4 см
- Четырёхаршинная сажень = 4 аршина = 284,48 см
| : неверное или отсутствующее изображение | В этом разделе не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 16 сентября 2012 года . |
К:Википедия:Статьи без источников (тип: не указан)
Японская система
- Мо = 0.003030303 см
- Рин = 0.03030303 см
- Бу = 0.3030303 см
- Сун = 3.030303 см
- Сяку = 30.30303 см
- Кэн = 181.8182 см
- Хиро = 181.8182 см
- Дзё = 303.0303 см
- Тё = 10909.09 см
- Ри = 392727.3 см
Древнегреческая система
- Палайста = 7 см
- Плетр = 31 м
- Миля = 1,388 км
- Стадий = 185,136 м
- Плетр = 30,856 м
- Амма = 18,514 м
- Акена (декапод) = 3,086 м
- Оргия (гексапод) = 1,851 м
- Бема (шаг) = 77,14 см
- Пехис (локоть) греческий = 61,712 см
- Пехис (локоть) короткий = 46,284 см
- Пус (фут) = 30,856 см
- Спитам = 23,142 см
- Дихас = 15,428 см
- Палестра (ладонь) = 7,714 см
- Кондиль = 3,857 см
- Дактиль (палец) = 1,928 см
- Стадий олимпийский = 192,27 м
- Стадий аттический = 184,98 м
- Стадий птолемеевский = 185 м
Типографическая система
- твип = 1/20 пункта
- пункт = 0,352777… мм (пункт Adobe) или 0,3759 мм (пункт Дидо) или 0,3515 мм (пункт Хоукса) или 0,375 мм (метрический пункт) или 0,3473 мм (пункт Фурнье)
- цицеро = 12 пунктам (= 4,2333… мм в системе Adobe)
- нонпарель = 5,708 пунктов
Флотская система
- Морская миля = 1852,000 м (международная) или 1853,184 м (британская)
- Кабельтов = 185,2000 м (международный) или 182,88 м = 100 морским саженям
- Морская сажень, фатом = 1,8288 м = 6 футам
Единицы, применяемые в астрономии
- радиус Луны (R
☾) = 1737,10 км; - радиус Земли (R
⊕) = 6371,0 км; - радиус Юпитера (R
♃ или
R
J) = 69 911 км; - световая секунда = 299 792 458 м ;
- радиус Солнца (R
☉) = 6,9551·105 км; - световой месяц = 783934206048416.66… м
- световая минута = 17 987 547 480 м ;
- астрономическая единица = 149 597 870,700 км [2];
- спат (единица длины) (англ.
) = 1·1012 м; - световой час = 1 079 252 848 800 м ;
- световые сутки = 25 902 068 371 200 м ;
- световая неделя = 181 314 478 598 400 м ;
- световой год = 9 460 730 472 581 000 м ;
- парсек = (648 000/π) а.е. (точно) ≈ 206264,806247 а.е. = 3,08567758491·1016 м;
- сириометр = 106 а.е. = 149 597 870 700 000 000 м[3];
Единицы, набранные малым шрифтом, практически не используются или устарели.
Единицы, применяемые в физике
- планковская длина ≈ 1,616199(97)·10−35[4][5][6];
- ферми = 1 фм = 1·10−15 м;
- классический радиус электрона = 2,8179402894(58)·10−15 м;
- икс-единица = 1,00207·10−13 м;
- комптоновская длина волны электрона = 2,4263102175(33)·10−12 м;
- боровский радиус = 5,2917720859(36)·10−11 м;
- ангстрем = 1·10−10 м;
Единицы, применяемые в технике
- юнит = 44,45 мм = 1,75 дюйма;
Таблица 4 класс: скорость, время, расстояние
В таблице ниже приведены данные для которых нужно придумать задачи, а потом их решить.
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Вы можете пофантазировать и придумать задачи к таблице сами. Ниже наши варианты условия задач:
- Мама отправила Красную Шапочку к бабушке. Девочка постоянно отвлекалась и шла по лесу медленно, со скоростью 5 км/час. На путь она потратила 2 часа. Какое расстояние за это время прошла Красная Шапочка?
- Почтальон Печкин вез на велосипеде посылку со скоростью 12 км/час. Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу?
- Папа Ксюши купил автомобиль и решил отвезти семью на море. Машина ехала со скоростью 60 км/час и на дорогу было потрачено 4 часа. Какое расстояние между домом Ксюши и морским побережьем?
- Утки собрались в клин и полетели в теплые края. Птицы махали крыльями без устали 3 часа и преодолели за это время 300 км. Какой была скорость птиц?
- Самолет АН-2 летит со скоростью 220 км/час. Он вылетел из Москвы и летит в Нижний Новгород, расстояние между этими двумя городами 440 км. Сколько времени самолет будет в пути?
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Примечания[ | ]
- Деньгуб В. М., Смирнов В. Г.
Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 77—82. — 240 с. — ISBN 5-7050-0118-5. - Согласно новому определению астрономической единицы, принятому МАС в сентябре 2012 г.
- WolframAlpha (неопр.)
. Архивировано 10 апреля 2013 года. - В скобках указано стандартное отклонение. Таким образом, значение планковской длины можно представить в следующих формах: ℓ P {displaystyle ell _{P}} ≈ 1,616199(97) · 10−35 м = = (1,616199 ± 0,000097) · 10−35 м = = [1,616102 ÷ 1,616296] · 10−35 м
- NIST, «Planck length» (англ.), NIST’s published CODATA constants
- Fundamental Physical Constants — Complete Listing
Общая формула
Скорость, время, расстояние — это 3 фундаментальных величины, связанные друг с другом. Исследуя одну характеристику, обязательно нужно учитывать две других. Фактически скорость — это физическая величина, определяющая, какую длину преодолеет физическое тело за единицу времени. Например, значение 120 км/ч показывает, что объект сможет преодолеть 120 километров за один час. В математическом виде связь между тремя характеристиками может быть записана в виде следующей формулы:
S = V * t, где:
- S — пройденное объектом расстояние;
- V — средняя скорость тела;
- t — время, затраченное на преодоление пути.
Зная это равенство и любых 2 параметра, можно выполнить расчёт третьего, так для времени она будет иметь вид t = S / V, а скорости V = S / t. Проверить правильность формулы для скорости времени и расстояния можно путём анализа размерности. Если в выражение подставить единицы измерения, то после сокращения должна получиться величина, соответствующая определяемой. S = V * t = (м / с) * с = м (метр). Что и требовалось получить. Аналогично можно проверить и 2 оставшиеся формулы: t = s / v = м / (м/с) = м * с / м = с (секунда) и V = S / t = м / с (метр на секунду).
Действительно, пусть имеется физическое тело, находящееся в каком-то месте. Через некоторое время, неважно по каким причинам, оно переместилось в другую точку, при этом не выходя за пределы установленного пространства. Если тело представить в декартовой плоскости, причём за начало принять координату (0, 0), через время объект изменит своё положение, определяющееся значением (x1, y2). В двухмерном же пространстве это изменение можно описать как переход из точки A в Б.
Значит, чтобы тело достигло второй координаты, ему необходимо затратить время. При этом пройденный путь будет находиться в прямой зависимости от него. Расстояние и время должны связываться третьей величиной, которой как раз и является скорость. То есть параметр, определяющий, за сколько тело сможет преодолеть определённую длину.
Как видно, выражение, связывающее 3 величины, довольно простое. Но оно не учитывает, что скорость может быть непостоянной, поэтому если объект проходит свой путь неравномерно, в выражение подставляют среднее значение. Находится оно как сумма всех отдельных скоростей на неравномерных участках: Vср = ΔS / Δt.