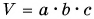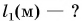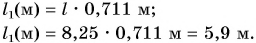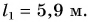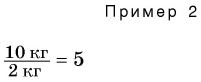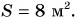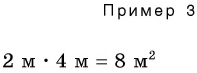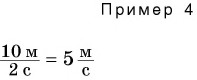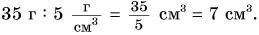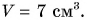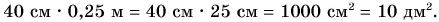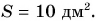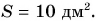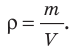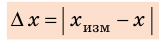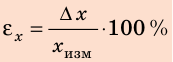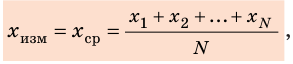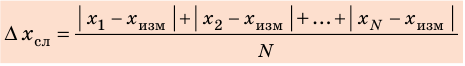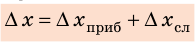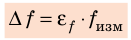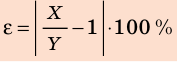Найди верный ответ на вопрос ✅ «Как пишется буквами: Масса, путь, скорость, перемещение, объем, плотность, время. И в чем они измеряются? (м, м3, м/с, км/м3, с, кг,) …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » ⭐️ Физика » Как пишется буквами: Масса, путь, скорость, перемещение, объем, плотность, время. И в чем они измеряются? (м, м3, м/с, км/м3, с, кг,)
Как пишется буквами: Масса, путь, скорость, перемещение, объем, плотность, время.
И в чем они измеряются? (м, м3, мс, кмм3, с, кг, )
как пишется буквами: Масса, путь, скорость, перемещение, объем, плотность, время.
И в чем
Задать свой вопрос
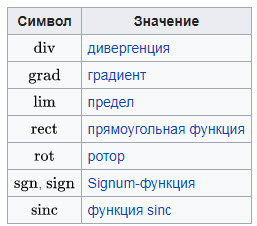
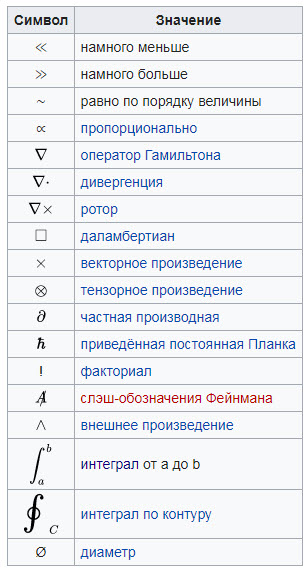
Символ Значение и происхождение Площадь (лат. area), векторный потенциал[1], работа (нем. Arbeit), амплитуда (лат. amplitudo), параметр вырождения, Работа выхода (нем. Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число Ускорение (лат. acceleratio), амплитуда (лат. amplitudo), активность (лат. activitas), коэффициент температуропроводности, вращательная способность, радиус Бора, натуральный показатель поглощения света Вектор магнитной индукции[1], барионный заряд (англ. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы Вектор магнитной индукции[1], красивый кварк (англ. beauty/bottom quark), постоянная Вина, ширина распада (нем. Breite) Электрическая ёмкость (англ. capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), очарование (чарм, шарм; англ. charm), коэффициенты Клебша — Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона — Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura) Скорость света (лат. celeritas), скорость звука (лат. celeritas), Теплоёмкость (англ. heat capacity), очарованный кварк (англ. charm quark), концентрация (англ. concentration), первая радиационная постоянная, вторая радиационная постоянная, удельная теплоёмкость Вектор электрической индукции[1] (англ. electric displacement field), Коэффициент диффузии (англ. diffusion coefficient), Оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, D-мезон (англ. D meson), Диаметр (лат. diametros, др.-греч. διάμετρος) Расстояние (лат. distantia), Диаметр (лат. diametros, др.-греч. διάμετρος), дифференциал (лат. differentia), нижний кварк (англ. down quark), дипольный момент (англ. dipole moment), период дифракционной решётки, толщина (нем. Dicke) Энергия (лат. energīa), напряжённость электрического поля[1] (англ. electric field), Электродвижущая сила (англ. electromotive force), магнитодвижущая сила, освещенность (фр. éclairement lumineux), излучательная способность тела, модуль Юнга Основание натуральных логарифмов (2,71828…), электрон (англ. electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия Сила (лат. fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор электромагнитного поля, магнитодвижущая сила, модуль сдвига, фокусное расстояние (англ. focal length) Частота (лат. frequentia), функция (лат. functia), летучесть (нем. Flüchtigkeit), сила (лат. fortis), фокусное расстояние (англ. focal length), сила осциллятора, коэффициент трения Гравитационная постоянная (англ. gravitational constant), тензор Эйнштейна, свободная энергия Гиббса (англ. Gibbs free energy), метрика пространства-времени, вириал, парциальная мольная величина, поверхностная активность адсорбата, модуль сдвига, полный импульс поля, Глюон (англ. gluon), константа Ферми, квант проводимости, электрическая проводимость, Вес (нем. Gewichtskraft) Ускорение свободного падения (англ. gravitational acceleration), Глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, Гравитон (англ. graviton), метрический тензор Напряжённость магнитного поля[1], эквивалентная доза, энтальпия (англ. heat contents или от греческой буквы «эта», H — ενθαλπος[2]), гамильтониан (англ. Hamiltonian), функция Ганкеля (англ. Hankel function), функция Хевисайда (англ. Heaviside step function), бозон Хиггса (англ. Higgs boson), экспозиция, полиномы Эрмита (англ. Hermite polynomials) Высота (нем. Höhe), постоянная Планка (нем. Hilfsgröße[3]), спиральность (англ. helicity) сила тока (фр. intensité de courant), интенсивность звука (лат. intēnsiō), интенсивность света (лат. intēnsiō), сила излучения, сила света, момент инерции, вектор намагниченности Мнимая единица (лат. imaginarius), единичный вектор (координатный орт) Плотность тока (также 4-вектор плотности тока), момент импульса, функция Бесселя, момент инерции, полярный момент инерции сечения, вращательное квантовое число, сила света, J/ψ-мезон Мнимая единица (в электротехнике и радиоэлектронике), плотность тока (также 4-вектор плотности тока), единичный вектор (координатный орт) Каона (англ. kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона, кинетическая энергия Коэффициент (нем. Koeffizient), постоянная Больцмана, теплопроводность, волновое число, единичный вектор (координатный орт) Момент импульса, дальность полёта, удельная теплота парообразования и конденсации, индуктивность, функция Лагранжа (англ. Lagrangian), классическая функция Ланжевена (англ. Langevin function), число Лоренца (англ. Lorenz number), уровень звукового давления, полиномы Лагерра (англ. Laguerre polynomials), орбитальное квантовое число, энергетическая яркость, яркость (англ. luminance) Длина (англ. length), длина свободного пробега (англ. length), орбитальное квантовое число, радиационная длина Момент силы, масса (лат. massa, от др.-греч. μᾶζα, кусок теста), вектор намагниченности (англ. magnetization), крутящий момент, число Маха, взаимная индуктивность, магнитное квантовое число, молярная масса Масса, магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка Количество (лат. numerus), постоянная Авогадро, число Дебая, полная мощность излучения, увеличение оптического прибора, концентрация, мощность, сила нормальной реакции Показатель преломления, количество вещества, нормальный вектор, единичный вектор, нейтрон (англ. neutron), количество (англ. number), основное квантовое число, частота вращения, концентрация, показатель политропы, постоянная Лошмидта Начало координат (лат. origo) Мощность (лат. potestas), давление (лат. pressūra), полиномы Лежандра, вес (фр. poids), сила тяжести, вероятность (лат. probabilitas), поляризуемость, вероятность перехода, импульс (также 4-импульс, обобщённый импульс; лат. petere) Импульс (также 4-импульс, обобщённый импульс; лат. petere), протон (англ. proton), дипольный момент, волновой параметр, давление, число полюсов, плотность. Электрический заряд (англ. quantity of electricity), количество теплоты (англ. quantity of heat), объёмный расход, обобщённая сила, хладопроизводительность, энергия излучения, световая энергия, добротность (англ. quality factor), нулевой инвариант Аббе, квадрупольный электрический момент (англ. quadrupole moment), энергия ядерной реакции Электрический заряд, обобщённая координата, количество теплоты (англ. quantity of heat), эффективный заряд, добротность Электрическое сопротивление (англ. resistance), универсальная газовая постоянная, постоянная Ридберга (англ. R ydberg constant), постоянная фон Клитцинга, коэффициент отражения, сопротивление излучения (англ. resistance), разрешение (англ. resolution), светимость, пробег частицы, расстояние Радиус (лат. radius), радиус-вектор, радиальная полярная координата, удельная теплота фазового перехода, удельная рефракция (лат. rēfractiō), расстояние Площадь поверхности (англ. surface area), энтропия[4], действие, спин (англ. spin), спиновое квантовое число (англ. spin quantum number), странность (англ. strangeness), главная функция Гамильтона, матрица рассеяния (англ. scattering matrix), оператор эволюции, вектор Пойнтинга, крутизна передаточной характеристики Перемещение (итал. spostamento), странный кварк (англ. strange quark), путь, пространственно-временной интервал (англ. spacetime interval), оптическая длина пути Температура (лат. temperātūra), период (лат. tempus), кинетическая энергия, критическая температура, терм, период полураспада, критическая энергия, изоспин Время (лат. tempus), истинный кварк (англ. true quark), правдивость (англ. truth), планковское время Внутренняя энергия, потенциальная энергия, вектор Умова, потенциал Леннард-Джонса, потенциал Морзе, 4-скорость, электрическое напряжение Верхний кварк (англ. up quark), скорость, подвижность, удельная внутренняя энергия, групповая скорость Объём (фр. volume), электрическое напряжение (англ. voltage), потенциальная энергия, видность полосы интерференции, постоянная Верде (англ. Verdet constant) Скорость (лат. vēlōcitās), фазовая скорость, удельный объём Механическая работа (англ. work), работа выхода, W-бозон, энергия, энергия связи атомного ядра, мощность Скорость, плотность энергии, коэффициент внутренней конверсии, ускорение Реактивное сопротивление, продольное увеличение, X-бозон Переменная, перемещение, абсцисса (декартова координата), молярная концентрация, постоянная ангармоничности, расстояние Гиперзаряд, силовая функция, линейное увеличение, сферические функции, Y-бозон ордината (декартова координата) Импеданс, Z-бозон, атомный номер или зарядовое число ядра (нем. Ordnungszahl), статистическая сумма (нем. Zustandssumme), вектор Герца, валентность, полное электрическое сопротивление (импеданс), угловое увеличение, волновое сопротивление вакуума аппликата (декартова координата)
Среди прочих обозначений наиболее часто школьников интересует вопрос о том, как в математике обозначается скорость, время, расстояние. Связано это с тем, что обозначения этих величин (особенно — скорости) в учебниках по математике и физике можно увидеть различные: с чертой над буквой v (читается: [вэ]), со стрелкой над буквой v, а также буквы v, выделенные курсивом или жирным шрифтом.
Скорость в математике обозначается буквой v, но её написание принято различным для рукописного и печатного текста.
В рукописном тексте скорость движения обычно обозначается строчной (т.е. маленькой) прописной (т.е. не печатной, как в тексте из газеты, а написанной от руки так, как если бы писали письмо) буквой v. В учебниках по математике (т.е. в печатном тексте) обычно скорость движения обозначается печатной буквой v, прямой или выделенной курсивом. Такое обозначение принимается практически во всех задачах по математике, исключение составляют лишь задачи, иллюстрирующие тему «Векторы» (в этом случае обозначение принимается таким же, как и в физике).
В физике (а точнее – в её разделе «механика») обозначение скорости зависит от того, нужно ли в данной задаче учитывать тот факт, что скорость – величина векторная. Там, где учитывать это не нужно, скорость обозначается строчной буквой v (печатной или прописной, так же, как и в математике). Если же необходимо учитывать то, что скорость характеризуется не только модулем (т.е. величиной), но и направлением, скорость изображается либо прописной буквой v с направленной слева направо стрелкой над этой буквой, либо той же прописной буквой v с горизонтальной чертой над этой буквой. В печатном тексте в этом случае обычно скорость обозначают либо печатной строчной буквой v со стрелкой или чертой над буквой, либо печатной буквой v, выделенной жирным шрифтом (т.е. так: v).
Буквой v обозначают скорость движения тел. Для обозначения скорости света и скорости звука принята другая, отличная от обозначения скорости движения тел, буква. Скорость света обозначается буквой «с» (скорость света в вакууме составляет с = 2,9979х108 м/с = 2,9979х105 км/с). Скорость звука так же обозначается буквой с (читается: [цэ]).
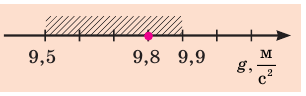
Ускорение обозначается буквой а (исключение составляет лишь ускорение свободного падения, эта величина обозначается буквой g (читается [жэ]), g = 9,81 м/с2). Если необходимо подчеркнуть, что эта величина – векторная (например, это часто требуется в физике), то над буквой «а» изображается либо горизонтальная черта, либо горизонтальная стрелка (так же, как и при обозначении скорости). В печатном тексте для обозначения ускорения как векторной величины может использоваться и буква «а», выделенная жирным шрифтом.
Если при решении задачи по физике или математике необходимо обозначить время, то это пишется буквой так: t (читается: [тэ]), а если расстояние — пишется буквой так: s (читается: [эс]). Для обозначения пути обычно используется строчная (маленькая) буква [эль], т.е. l, реже — заглавная (большая) буква [эль], т.е. L. Чтобы обозначение пути «l» не было похоже на «единицу», эту букву пишут курсивом, т.е. с наклоном.
Вообще, вопросы «как в математике пишется скорость», «как в математике пишется время», «как в математике пишется расстояние» некорректны. Лучше формулировать такой вопрос, употребляя не слово «пишется», а слово «обозначается».
Источники:
- Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике для инженеров и студентов вузов
- Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра/ Под ред. П.Ф. Фильчакова
- Каплан И.А. Практические занятия по высшей математике
Дополнительная информация:
- ru.wikipedia.org – Список обозначений в физике
- azbyka.kz — Урок математики «Скорость, время, расстояние»
Содержание:
Явления природы и свойства тел в физике описывают с помощью терминов, например: движение, траектория, состояние спокойствия. Описывая движение (рис. 4.1), можно указать, куда движется тело (вперед, назад или вверх), большое оно или маленькое; движется по пря-мой или поворачивает (влево или вправо), а может, вообще не движется. Такая характеристика движения является качественной.
Нас интересуют и количественные характеристики: с какой скоростью двигался автомобиль, какое расстояние он проехал. Количественной характеристикой тела или явления является физическая величина. Физическая величина описывает определенное свойство тела или явления. Она характеризуется числовым значением и единицей измерения. Например: автомобиль проехал путь в 30 километров. Сокращенно можно записать S = 30 км.
Каждая физическая величина имеет свое на-звание и символ, которым она обозначается.
Чтобы описать явление падения определенного тела, можно применить такие физические величины, как масса тела, высота, время падения. Физические величины обычно обозначают латинскими или греческими буквами. Массу тела обозначают буквой «m», высоту – буквой «h», время – буквой «t». Например, если тело массой 2 килограмма упало с высоты 5 метров за одну секунду, то пишут: m = 2 кг, h = 5 м, t = 1 с, употребляя общепринятые сокращения: кг – килограмм, м – метр, с – секунда.
Если нас интересует единица измерения физической величины, а не ее числовое значение, то эту величину пишут в квадратных скобках. Например, диаметр трубы составляет d = 3,2 см, а название единицы измерения (размерность): [d] =см.
Почему нужно измерять:
Начертите на листе бумаги горизонтальный отрезок. Потом проведите от середины этого отрезка перпендикулярный к нему отрезок такой же длины «на глаз». Измерьте длину отрезков линейкой, и вы убедитесь, что вертикальный отрезок короче. Вот почему нужно проводить измерения.
Средства измерения
Прямые измерения физических величин осуществляют с помощью приборов. Длину измеряют линейкой, время – с помощью часов, массу – на весах. Для определения размеров очень малых тел или больших расстояний используют более сложные приборы. Измерить физическую величину – значит сравнить ее с определенной мерой, которая является копией общепринятого образца-эталона. Эталонов немного, и хранятся они в специальных метрологических лабораториях.
История:
Для измерения времени использовали вытекание или капанье воды в сосуд с делениями или пересыпание песка – водяные или песочные часы (рис. 4.2). Движение Солнца по небу давало возможность измерять время с помощью солнечных часов (рис. 4.3). Такими часами люди пользовались несколько тысячелетий, однако они имели существенный недостаток – были довольно неточными.
Рис. 4.3. Солнечные часы
В настоящее время появились очень точные кварцевые часы, которые отсчитывают время в на-ручных часах, мобильном телефоне или компьютере. Для потребностей навигации и науки используют атомные часы, которые «ходят» настолько точно, что допускают ошибку в одну секунду за 500 000 лет!
Для измерения длины надо иметь образец, дли-на которого соответствует общепринятым единицам измерения. Сейчас это 1 м. Эталон (образец) метра хранится в метрологических лабораториях, главная из которых находится в г. Севре (Франция). Измерить длину можно еще и в других единицах измерения – канцелярскими скрепками, например, или спичками и сказать: мой рост составляет 80 скрепок или 36 спичечных коробков. Однако у других людей скрепки или спички могут оказаться другого размера, что усложнит обмен информацией. В давние времена так и было: пользовались футами (длина ступни – 30 см), дюймами (длина последней фаланги большого пальца, приблизительно 2,5 см), ярдами, пядями, саженями, локтями.
Инициаторами перехода на метрическую систему единиц были французы. Согласно договоренности, один метр определили как одну сорокамиллионную часть длины меридиана, который проходит через Париж. Для определения длины меридиана достаточно было измерять его часть, которая простирается от юга Испании до севера Норвегии. Начался этот процесс во время Великой французской революции. Днем рождения метрической системы мер считают 10 декабря 1799 г.
На территории нашей страны метрическая система мер была введена специальным декретом 14 сентября в 1918 г. Переход на новые стандарты измерений связан с изменением привычек, необходимостью переиздания справочников, переоборудования метрических лабораторий, с переподготовкой персонала и тому подобным. Все это стоит довольно дорого. США, например, переход на новые стандарты обошелся в 11 млрд. долларов.
Международная система единиц измерения – СИ
В связи с потребностью международного сотрудничества в 1960 году большинство стран мира подписали соглашение о единой Международной системе еди-ниц измерения SI – Systeme International (на русском языке – СИ).
Рис. 4.4. Эталон метра хранится в Международном бюро мер и весов в Париже
Рис. 4.5. Эталон килограмма
В СИ есть 7 основных единицы измерения, которые обеспечены соответствующими эталонами. Остальные единицы измерения могут быть выражены через основные единицы. Для начала нам понадобятся три основные единицы: метр, килограмм и секунда.
Эталон метра изображен на рис. 4.4. Это рельс определенного профиля, длина которого составляет одну сорокамиллионную часть меридиана, проходящего через Париж. Первый эталон метра был изготовлен во Франции в 1795 году.
В 1983 году эталон длины был изменен: теперь метр определен как расстояние, которое проходит свет в вакууме за 1/299 792 458 долю секунды.
Эталон килограмма – цилиндр из платиново-иридиевого сплава, высота которого равна его диаметру и составляет 39 мм (рис. 4.5).
С эталоном секунды вы ознакомитесь в 11 классе.
Таблица 4.1
| Величина | Символ | Размерность | |
| рус. | междунар. | ||
| Длина | l | м | m |
| Масса | m | кг | kg |
| Время | t | с | s |
| Площадь | S, | м2 | m2 |
| Объем | V | м3 | m3 |
| Скорость | v | м/с | m/s |
Площадь в СИ измеряют в м2 (квадратные метры), объем – в м3 (кубические метры).
В таблице 4.1 единицы площади, объема и скорости являются производны-ми единицами, их размерности происходят от основных единиц измерения.
В расчетах используют также кратные и дольные единицы.
Кратные единицы – это единицы, которые больше основных единиц в 10, 100, 1000 и больше раз. Например: 1 дм = 10 см = 101 см, 1 м = 100 см = 102 см, 1 км = 1000 м = 103 м, 1 кг = 1000 г = 103 г.
Дольные единицы – это единицы, которые меньше основных единиц в 10, 100, 1000 и больше раз: 1 см = 0,01 м = 10–2 м, 1 мм = 0,1 см = 10–1 см.
С единицами времени несколько иначе: 1 мин. = 60 с, 1 час = 3600 с. Дольными являются лишь 1 мс (миллисекунда) = 0,001 с = 10–3 с и 1 мкс (микросекунда)= = 0,000001 с = 10–6 с.
Для обозначения кратных и дольных единиц используют приставки (табл. 4.2).
Таблица 4.2 Приставки для обозначения кратных и дольных единиц
| Кратность | Приставка | Обозначение | Пример | ||
| русское | международное | русское | международное | ||
| 102 | гекто | hecto | г | h | 5 гПа (гектопаскаль) = = 500 Па |
| 103 | кило | kilo | к | k | 6 кг (килограмм) = 6000 г |
| 106 | мега | mega | М | M | 2 МДж (мегаджоуль) = = 2 000 000 Дж |
| 109 | гига | giga | Г | G | 1 ГГц (гигагерц) = = 1 000 000 000 Гц |
| Дольность | |||||
| 10–1 | деци | deci | д | d | дм – дециметр |
| 10–2 | санти | centi | с | c | см – сантиметр |
| 10–3 | милли | milli | м | м | мл – миллилитр |
| 10–6 | микро | micro | мк | µ | мкм – микрометр, микрон |
| 10–9 | нано | nano | н | n | нм – нанометр |
Итоги
- Физические величины количественно описывают свойства тел и явлений.
- Физические величины характеризуются названием, символом, числовым значением и единицей измерения.
- В международной системе единиц измерения (СИ) основные механические единицы измерения физических величин – метр, килограмм и секунда.
- Измерить физическую величину – значит сравнить ее с мерой-эталоном.
Физические величины
Физические тела и явления характеризуют физическими величинами. Некоторые из них вам уже знакомы из курса природоведения: это длина, площадь, объем, масса, сила. Рассмотрим их подробнее.
В науке используют единицы физических величин, определенные Международной системой единиц, которую сокращенно называют1 SI — от английских слов System International, что означает «международная система».
Длина, Площадь, Объем
Длиной характеризуют физические тела и, например, путь, пройденный телом за время его движения. За единицу длины в SI принят2 I метр (м).
На линейках и мерных лентах (рулетках) нанесены деления, обозначающие сотые и тысячные доли метра — сантиметры и миллиметры (рис. 3.1).
Единицы площади и объема определяют с помощью единицы длины: единицей площади является I м2 (площадь квадрата со стороной I м), а единицей объема — I м3 (объем куба с ребром I м).
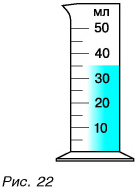
Объем жидкости измеряют с помощью измерительных цилиндров, называемых часто мензурками (рис. 3.2). Длину, площадь и объем задают их числовыми значениями. Физические величины, которые задают только числовыми значениями, называют скалярными.
Время
Всякое физическое явление длится в течение определённого промежутка времени. За единицу времени в S1 принята 1 секунда (с), 60 с составляют 1 минуту (мун), а 60 минут — 1 час (ч).
Время измеряют часами (рис. 3.3). Они представляют собой обычно устройства, в которых повторяется определенный процесс. Например, в маятниковых часах повторяются колебания маятника. Сегодня чаще используют кварцевые часы, в которых колеблются крошечные кристаллы кварца.
Перемещение и скорость
При движении тело изменяет свое положение в пространстве.
Перемещением тела называют направленный отрезок, проведенный из начального положения тела в его конечное положение.
Перемещение задают числовым значением (длиной указанного отрезка) и направлением. Физические величины, которые характеризуют числовым значением и направлением, называют векторными:
Значение векторной величины называют ее модулем.
Векторную величину обозначают буквой со стрелкой, а модуль — той же буквой без стрелки. Так, перемещение обычно обозначают 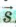

Скоростью тела называют физическую величину, равную отношению перемещения тела к промежутку времени, в течение которого произошло это перемещение.
Скорость, как и перемещение, является векторной величиной, то есть ее характеризуют модулем и направлением. Например, скорости двух встречных автомобилей могут быть равными по модулю, но направлены они противоположно. Скорость обозначают обычно 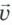
Единицей скорости в SI является 1 метр в секунду (м/с). Тело, которое движется с такой скоростью, за 1 с перемещается на 1 м, — это скорость прогулки. Рекорд скорости в беге — чуть больше 10 м/с.
Скорость современных реактивных самолетов достигает почти километра в секунду (км/с), а космических кораблей — даже больше 10 км/с. Но ни одно тело не может двигаться со скоростью, превышающей скорость света в вакууме, которая равна примерно 300 000 км/с.
Для измерения скорости автомобилей и мотоциклов используют спидометры1 (рис. 3.4-3.6). Они показывают обычно скорость в километрах в час (км/ч). Вы, наверное, замечали, что во время движения автомобиля стрелка спидомстра обычно «покачивается». Дело в том, что скорость автомобиля при движении обычно изменяется.
Масса
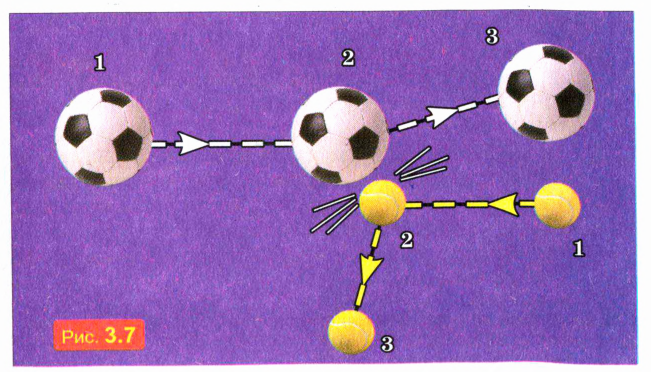
Каждое физическое тело имеет определенную массу. Массы двух тел можно сравнить, измерив, как изменяются их скорости при взаимодействии друг с другом: скорость тела большей массы изменяется меньше, чем скорость тела меньшей массы.
Например, на рис. 3.7 схематически показано столкновение, футбольного и теннисного мячей (цифры обозначают положение мячей в три последовательных момента времени). Мы видим, что при столкновении скорость футбольного мяча изменилась намного меньше, чем скорость теннисного. Значит, масса футбольного мяча намного больше массы теннисного мяча.
Далее мы расскажем о намного более простом способе измерения массы тел, который обычно и используют на практике.
Единицей массы в S1 является 1 килограмм (кг). Это примерно масса одного литра воды. Международный эталон килограмма представляет собой металлический цилиндр из специального сплава.
Сила
Мерой взаимодействия тел является сила: чем больше сила, действующая на тело, тем больше изменяется скорость этого тела за 1 с. Сила является векторной величиной: ее задают числовым значением и направлением. На рисунках силу обозначают стрелкой, начало которой находится в точке приложения силы.
Единицу силы в честь Ньютона назвали ньютоном (Н)1. Сила в 1 Н, приложенная к движущемуся телу массой 1 кг в направлении движения тела, увеличивает его скорость за каждую секунду на 1 м/с,
Чтобы вы представили себе, что такое сила в 1 Н, приведем пример: когда вы держите полное ведро воды, то прикладываете к нему силу, равную примерно 100 Н. При этом приложенная вами сила уравновешивает силу, с которой Земля притягивает то же самое ведро с водой.
Силу, с которой Земля притягивает предметы, называют силой тяжести. В многочисленных опытах было установлено, что сила тяжести, действующая на тело, пропорциональна его массе.
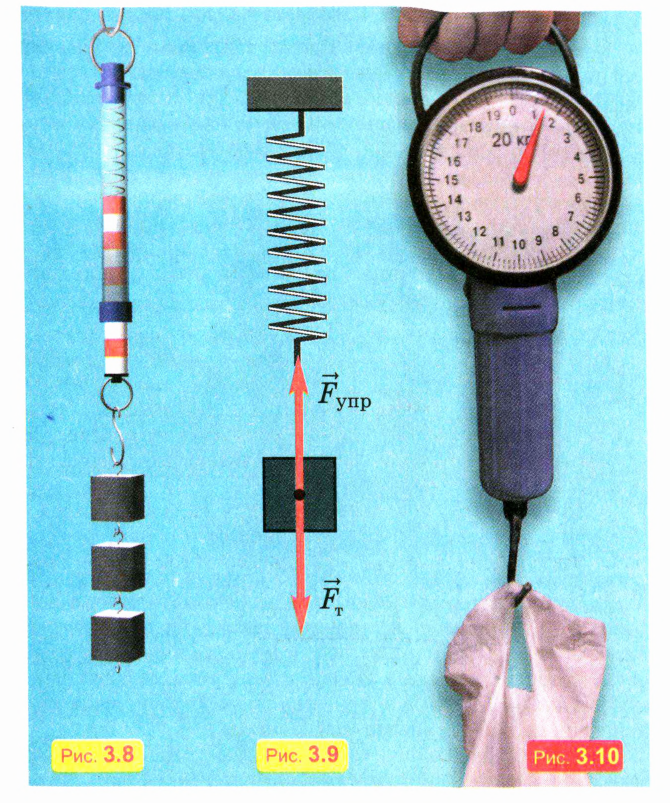
Силу измеряют динамометром2. На рис. 3.8 показан пружинный динамометр, действие которого основано на том, что удлинение пружины пропорционально значению растягивающей ее силы.
На рис. 3.9 схематически изображены силы, действующие на тело, подвешенное к динамометру: это сила тяжести со стороны Земли и сила упругости со стороны пружины. Если тело находится в покое, сила упругости уравновешивает силу тяжести, то есть направлена противоположно ей и равна ей по модулю.
Значит, по удлинению пружины в этом случае можно найти значение силы тяжести. А это, в свою очередь, позволяет рассчитать массу тела, поскольку сила тяжести пропорциональна массе тела.
Таким образом, массу тела можно найти с помощью взвешивания. Пружинные весы (рис. 3.10) — это динамометр, шкала которого размечена (проградуирована) так, что она показывает массу подвешенного груза.
Что называется физической величиной
Издавна люди для более точного описания каких-нибудь событий, явлений, свойств тел и веществ используют их характеристики. Например, сравнивая тела, которые нас окружают, мы говорим, что книга меньше, чем книжный шкаф, а конь больше кошки. Это означает, что объем коня больше объема кошки, а объем книги меньше объема шкафа.
Объем — пример физической величины, которая характеризует общее свойство тел занимать ту или иную часть пространства (рис. 1.15, а). При этом числовое значение объема каждого из тел индивидуально.
Рис. 1.15. Для характеристики свойства тел занимать ту или иную часть пространства мы используем физическую величину объем (а, б), для характеристики движения — скорость (б, в)
Общая характеристика многих материальных объектов или явлений, которая может приобретать индивидуальное значение для каждого из них, называется физической величиной.
Еще одним примером физической величины может служить известное вам понятие «скорость*. Все движущиеся тела изменяют свое положение в пространстве с течением времени, однако быстрота этого изменения для каждого тела различна (рис. 1.15, б, в). Так, самолет за 1 с полета успевает изменить свое положение в пространстве на 250 м, автомобиль — на 25 м, человек — на 1 м, а черепаха — всего на несколько сантиметров. Поэтому физики и говорят, что скорость — это физическая величина, которая характеризует быстроту движения.
Нетрудно догадаться, что объем и скорость,— это далеко не все физические величины, которыми оперирует физика. Масса, плотность, сила, температура, давление, напряжение, освещенность — это лишь малая часть тех физических величин, с которыми вы познакомитесь, изучая физику.
Что означает измерить физическую величину
Для того чтобы количественно описать свойства какого-либо материального объекта или физического явления, необходимо установить значение физической величины, которая характеризует данный объект или явление.
Значение физических величин получают путем измерений (рис. 1.16— 1.19) или вычислений.
Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу.
Приведем пример из художественной литературы: «Пройдя шагов триста по берегу реки, маленький отряд вступил под своды дремучего леса, извилистыми тропами которого им надо было странствовать на протяжении десяти дней*. (Ж. Верн «Пятнадцатилетний капитан*)
Герои романа Ж. Верна измеряли пройденный путь, сравнивая его с шагом, то есть единицей измерения служил шаг. Таких шагов оказалось триста. В результате измерения было получено числовое значение (триста) физической величины (пути) в избранных единицах (шагах).
Рис. 1.20. Если бабушка и внук будут измерять расстояние в шагах. то они всегда будут получать разные результаты
Очевидно, что выбор такой единицы не позволяет сравнивать результаты измерений, полученные разными людьми, поскольку длина шага у всех разная (рис. 1.20). Поэтому ради удобства и точности люди давным-давно начали договариваться о том, чтобы измерять одну и ту же физическую величину одинаковыми единицами. Ныне в большинстве стран мира действует принятая в I960 году Международная система единиц измерения, которая носит название «Система Интернациональная* (СИ) (рис. 1.21).
В этой системе единицей длины является метр (м), времени — секунда (с); объем измеряется в метрах кубических (м3), а скорость — в метрах в секунду (м/с). Об остальных единицах СИ вы узнаете позже.
Кратные и дольные единицы
Из курса математики вы знаете, что для сокращения записи больших и малых значений разных величин пользуются кратными и дольными единицами.
Кратные единицы — это единицы, которые больше основных единиц в 10, 100, 1000 и более раз.
Дольные единицы — это единицы, которые меньше основных в 10, 100, 1000 и более раз.
Для записи кратных и дольных единиц используют приставки. Например, единицы
Рис. 1.21. Основные единицы Международной системы (СИ)
длины, кратные одному метру,— это километр (1000 м), декаметр (10 м). Единицы длины, дольные одному метру,— это дециметр (0,1 м), сантиметр (0,01 м), микрометр (0,000001 м) и так далее.
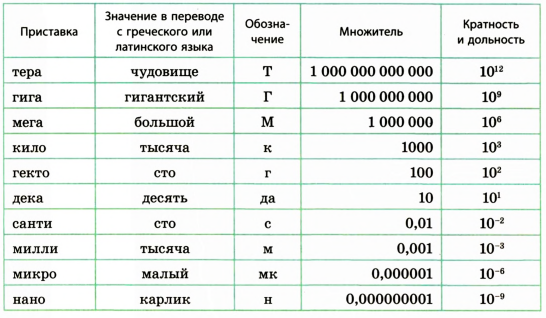
В таблице приведены наиболее часто употребляемые приставки.
Приставки, служащие для образования кратных и дольных единиц
Измерительные приборы
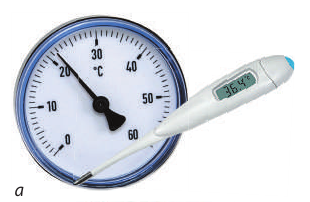
Измерение физических величин ученые проводят с помощью измерительных приборов. Простейшие из них — линейка, рулетка — служат для измерения расстояния и линейных размеров тела. Вам также хорошо известны такие измерительные приборы, как часы — прибор для измерения времени, транспортир — прибор для измерения углов на плоскости, термометр — прибор для измерения температуры и некоторые другие (рис. 1.22, с. 20). Со многими измерительными приборами вам еще предстоит познакомиться.
Большинство измерительных приборов имеют шкалу, которая обеспечивает возможность измерения. Кроме шкалы, на приборе указывают единицы, в которых выражается измеренная данным прибором величина*.
По шкале можно установить две наиболее важные характеристики прибора: пределы измерения и цену деления.
Пределы измерения — это наибольшее и наименьшее значения физической величины, которые можно измерить данным прибором.

————————————————
Цена деления — это значение наименьшего деления шкалы измерительного прибора.
Например, верхний предел измерений медицинского термометра (рис. 1.23) равен 42 °С, нижний — 34 °С, а цена деления шкалы этого термометра составляет 0,1 °С.
Напоминаем: чтобы определить цену деления шкалы любого прибора, необходимо разность двух любых значений величин, указанных на шкале, разделить на количество делений между ними.
Итоги:
Общая характеристика материальных объектов или явлений, которая может приобретать индивидуальное значение для каждого из них, называется физической величиной.
Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу.
В результате измерений мы получаем значение физических величин.
Говоря о значении физической величины, следует указать ее числовое значение и единицу.
Для измерения физических величин пользуются измерительными приборами.
Для сокращения записи числовых значений больших и малых физических величин используют кратные и дольные единицы. Они образуются с помощью приставок.
Точность измерений
Теперь вы знаете, что означает измерить физическую величину. И в повсе дневной жизни вам уже приходилось выполнять множество простейших измерений. Но насколько точными были ваши измерения? Можно ли получить абсолютно точное значение физической величины?
Попробуем разобраться в этих непростых вопросах.
Оцениваем размеры и проверяем результат:
Начнем с проверки вашего глазомера.
Оцените на глаз длину иглы, изображенной на рис 1.24. А теперь давайте проверим, насколько результат вашей оценки соответствует действительности, то есть измерим длину той же иглы с помощью линейки. Для этого:
- — приложим линейку к игле так, чтобы «ноль» на ее шкале совпал с одним концом иглы (рис. 1.25);
- — определим значение деления шкалы, напротив которого расположен ее другой конец.
Мы видим, что он расположен возле отметки 5 см. Отсюда делаем вывод, что длина иглы около 5 см. Если результат вашей предварительной оценки совпадает с этим значением, то у вас хороший глазомер. Определить на глаз размер более точно нам не удастся.
Результат измерений:
Если нам нужен более точный результат, придется обратить внимание на то, что кончик иглы немного более чем на два миллиметра выступает за отметку 5 см. Итак, более точная длина иглы — 5,2 см, или 52 мм.
Вы можете возразить, что это тоже неточно.
Да, неточно! Именно поэтому принято всегда указывать точность, с которой выполнено измерение.
В первом случае наше измерение выполнено с точностью до 1 см, а во втором — с точностью до 0,1 см.
Чтобы произвести еще более точное измерение, необходимо учесть длину той части иглы, которая выступает за отметку 52 мм, и тогда точность повысится до 0,01 см. Но для этого нам придется использовать измерительный прибор с еще меньшей ценой деления, то есть более точный, но даже тогда мы не можем утверждать, что измерили иглу совершенно точно.
Причин для этого достаточно: это и несовершенство конструкции прибора, и погрешности, которые возникают при проведении опыта (например, начало иглы невозможно абсолютно точно совместить с «нулем» линейки). Таким образом, даже если измерение проводится более тщательно и с помощью более совершенного прибора, точность возрастает, но погрешностей все равно не избежать.
Чтобы уменьшить погрешность, измерение можно выполнить несколько раз, а затем вычислить среднее значение всех полученных результатов (наити их среднее арифметическое).
Точность измерений
Однако не следует думать, что чем точнее измерение, тем лучше: излишняя точность не всегда целесообразна.
Предположим, что вместо длины иглы вам необходимо измерить длину крышки стола. В этом случае нет необходимости учитывать десятые и сотые доли миллиметра, поскольку, измеряя длину стола в разных местах, мы получим величины, отличающиеся на несколько миллиметров. Поэтому долями миллиметра в этом случае можно пренебречь. Также нет смысла измерять длину стены с точностью до одного миллиметра (рис. 1.26).
Из этого можно сделать вывод, что необходимую точность измерения определяет цель эксперимента.
Чаще всего важно не значение погрешности, а то, какую часть от всей измеренной величины составляет возможная погрешность.
Если портной, выкраивая брюки, ошибется на 1 мм, вы этого даже не заметите. А вот если, втягивая нить в ушко иглы, он всякий раз будет ошибаться на 1 мм (рис. 1.27), то едва ли брюки вообще когда-либо будут сшиты.
Роль измерений в физике. Прямые и косвенные измерения
Наука начинается с тех пор, как начинают измерять… Д. И. Менделеев
Вдумайтесь в слова известного ученого. Из них ясна роль измерений в любой науке, особенно в физике. Но, кроме того, измерения важны в практической жизни. Можете ли вы представить свою жизнь без измерений времени, массы, длины, скорости движения, расхода электроэнергии и т. д.?
Как измерить физическую величину? Для этой цели используются измерительные приборы. Некоторые из них вам уже известны. Это разного вида линейки, часы, термометры, весы, транспортиры и др.
Измерительные приборы бывают цифровые и шкальные. В цифровых приборах результат измерений определяется цифрами. Это электронные приборы — часы, термометр, счетчик электроэнергии (рис. 19) и др.
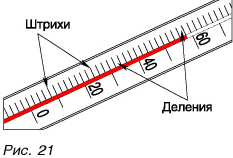
Линейка, стрелочные часы, термометр бытовой, весы, транспортир (рис. 20) — это шкальные приборы. Они имеют шкалу. По ней определяется результат измерений. Вся шкала расчерчена штрихами на деления (рис. 21). Одно деление это не один штрих, как иногда ошибочно считают некоторые учащиеся, а промежуток между двумя ближайшими штрихами. На рисунке 22 на шкале мензурки от значения 10 мл до значения 20 мл два деления, но три штриха. Приборы, которые мы будем использовать в лабораторных работах, в основном шкальные.
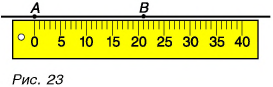
Что значит измерить физическую величину? Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу. Например, чтобы измерить длину отрезка прямой между точками A и В, нужно приложить линейку и по ее шкале (рис. 23) определить, сколько миллиметров укладывается между точками А и В. Однородной величиной, с которой проводилось сравнение длины отрезка АВ, в данном случае была длина, равная 1 мм.
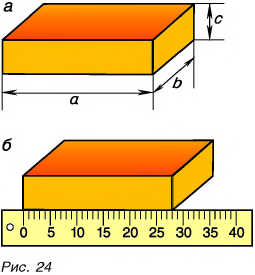
Если физическая величина измеряется непосредственно путем снятия данных со шкалы прибора, то такое измерение называют прямым. Например, приложив линейку к разным ребрам бруска, мы определим его длину а, ширину b и высоту с (рис. 24, а). Значение длины, ширины и высоты мы определили непосредственно, сняв данные со шкалы линейки. Из рисунка 24, б следует: a = 28 мм. Это прямое измерение.
А как определить объем бруска? Надо провести прямые измерения его длины а, ширины b и высоты с, а затем по формуле
вычислить объем бруска.
В этом случае мы говорим, что объем бруска определили по формуле, т. е. косвенно, и измерение объема называется косвенным измерением.
В физике измерения физических величин чаще всего косвенные. В дальнейшем вы убедитесь в этом сами.
Главные выводы:
- Измерительные приборы бывают цифровые и шкальные.
- При прямых измерениях физическая величина определяется непосредственно по шкале прибора.
- При косвенных измерениях физическая величина определяется по формуле.
Для любознательных:
Изучая строение человеческого тела и работу его органов, ученые проводят множество измерений. Оказывается, в человеке массой примерно 70 кг около 6 л крови. Сердце человека в спокойном состоянии сокращается 60—80 раз в минуту. За одно сокращение оно выбрасывает в среднем 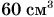
В течение суток кровь человека около 360 раз проходит через почки, очищаясь там от вредных веществ. Общая протяженность почечных кровеносных сосудов составляет приблизительно 18 км. Ведя здоровый образ жизни, мы помогаем нашему организму работать без сбоев!
Единицы измерения физических величин
Чтобы решить, как быстрее доехать до вокзала — на трамвае или на такси, сравнивают скорости движения этих транспортных средств. Скорость — физическая величина. Она количественно описывает физическое явление — движение. Если скорость автомобиля 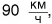
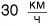
В физике для описания физических явлений и свойств используется множество физических величин: длина, сила, давление и др. Каждая физическая величина имеет символическое обозначение, числовое значение и единицу измерения. Например, длина бруска 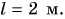
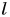
Исторически сложилось так, что у разных народов и государств единицы измерения одних и тех же физических величин различались. Часто это были единицы, соответствующие размерам частей тела человека, массе семени бобов и т. д. Пользоваться такими единицами было неудобно, особенно в торговле между разными государствами.
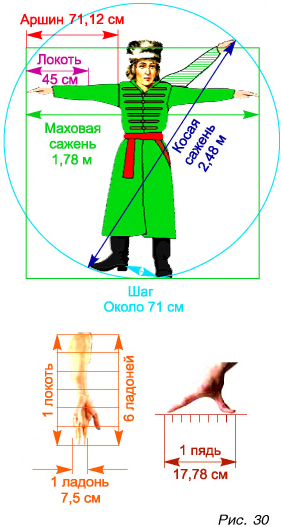
Например, в Англии для измерения длины использовался фут (1 фут = 30,5 см), а на Руси — аршин (1 аршин = 71,1 см) (рис. 30). Нужно было упорядочить систему единиц, сделать ее удобной в использовании всеми странами. В 1960 г. ввели единую Международную систему единиц (сокращенно СИ — Систему Интернациональную). Ею пользуется большинство стран. Основными единицами в СИ являются: метр (м) — для длины, килограмм (кг) — для массы, секунда (с) — для промежутка времени, Кельвин (К) — для температуры.
Но всегда ли удобно измерять время в секундах, а длину — в метрах? Оказывается, нет. Например, время движения поезда из Минска в Москву измеряют в часах (ч), а путь — в километрах (км). Единицы 1 ч и 1 км — это неосновные (кратные) единицы СИ. Между основными и неосновными единицами существует связь. Так, 1 км = 1000 м, 1 ч = 3600 с.
Основные единицы измерения имеют эталоны. Эталоны хранятся в г. Севре (Франция) в Международном бюро мер и весов. На рисунке 31 приведен эталон килограмма — цилиндр из плати но-иридиевого сплава. По эталону делают копии, которыми пользуются разные страны. Позже вы познакомитесь с эталонами других единиц измерения.
Для любознательных
Эталонная база страны обеспечивает единство измерений и является частью национального достояния. В Беларуси, как и в других странах, ведется работа по исследованию и созданию эталонных комплексов. В Белорусском государственном институте метрологии созданы эталоны массы, времени (см. рис.), температуры и др.
Главные выводы
- Каждая физическая величина имеет символическое обозначение, числовое значение и единицу измерения.
- Основными единицами СИ являются: метр, килограмм, секунда, Кельвин и др.
- Основные единицы измерения имеют свои эталоны.
Пример №1
В одной из книг немецкого путешественника XVII в. есть такие строки: «Шелковая материя, привозимая с Востока, называется русскими «китайкой», и каждый кусок содержит ни больше ни меньше как восемь с четвертью аршин». Сколько метров в куске материи?
Дано:
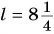
1 аршин = 71,1 см = 0,711 м
Решение
Так как 1 аршин = 71,1 см = 0,711 м, то длина восьми с четвертью аршин в метрах будет равна:
Ответ:
- Заказать решение задач по физике
Действия над физическими величинами
В математике можно складывать, вычитать и сравнивать любые числа. А какие действия можно производить над физическими величинами?
Действия сложения, вычитания и сравнения над физическими величинами можно производить только в том случае, если они однородны, т. е. представляют одну и ту же физическую величину.
Мы можем складывать длину с длиной, вычитать из массы массу, сравнивать промежуток времени с промежутком времени (пример 1). Смешно и нелепо было бы складывать 4 м и 5 кг или вычитать 30 с из 9 кг. А вот умножать и делить можно как однородные, так и разные физические величины.
В примере 2 делятся не только числовые значения (10 : 2 = 5), но и единицы физических величин (кг : кг = 1). Результат показывает, во сколько раз одна физическая величина (масса) больше другой.
В примере 3 умножаются числовые значения 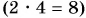
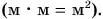
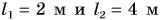
В примере 4 в результате деления двух разных физических величин — длины 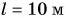
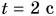
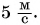
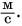
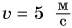
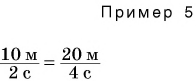
В примере 5 знак равенства относится не только к числовым значениям, но и к единицам. Знак равенства поставить нельзя, если сравнить 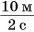
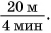
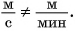
Для любознательных:
Большие единицы времени — год и сутки — дала нам сама природа. Но час, минута и секунда появились благодаря человеку.
Принятое в настоящее время деление суток восходит к глубокой древности. В Вавилоне применялась не десятичная, а шестидесятеричная система счисления. Поскольку 60 делится без остатка на 12, сутки у вавилонян состояли из 12 равных частей. В Древнем Египте было введено деление суток на 24 часа. Позже появились минуты и секунды. То, что в 1 часе 60 минут, а в 1 минуте 60 секунд, — наследие шестидесятеричной системы счисления Вавилона.
Главные выводы:
- Складывать, вычитать и сравнивать можно только однородные физические величины.
- Умножение и деление разнородных величин приводит к появлению новой физической величины.
Пример №2
Выберите значения физических величин, которые можно складывать: 120 г, 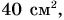
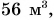
Решение
Однородными физическими величинами в данном случае являются массы тел: 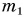
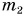
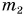
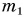
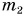
Следовательно, m = 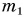
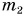
Ответ: результатом сложения является масса m = 168 г.
Пример №3
Определите физические величины, получившиеся в результате
выполнения следующих действий: 1) 35 г : 5 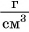
Решение
1) Найдем отношение двух физических величин, разделив их числовые значения и единицы:
Мы получили физическую величину — объем
2) Чтобы умножить две однородные физические величины, необходимо выразить их в одних единицах, например в сантиметрах (см):
Мы получили физическую величину — площадь
Ответ: 1) в результате деления двух физических величин разного рода (массы и плотности) получена третья физическая величина — объем 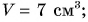
физические величины и их измерение
Чем отличается язык физики (и любой другой точной науки) от обычного? язык физики интернационален: он создавался лучшими умами человечества, его однозначно понимают в любом уголке нашей планеты. язык физики объективен: каждое его понятие однозначно, оно имеет один смысл, который может измениться (чаще всего — расшириться) только благодаря опытам. Как и методы научного познания, язык физики родился из практики.
Что такое физическое исследование и каковы его методы
Вспомним, с чего начинается исследовательская работа ученых. Прежде всего — это наблюдение за определенным явлением (телом или материалом) и размышления над его сущностью.
Наблюдение — это восприятие природы с целью получения первичных данных для последующего анализа. Далеко не всегда наблюдения приводят к правильным выводам. Поэтому, чтобы опровергнуть или подтвердить собственные выводы, ученые проводят физические исследования.
Физическое исследование — это целенаправленное изучение явлений и свойств природы средствами физики.
| Методы физических исследований | |
|---|---|
| экспериментальный | теоретический |
| Эксперимент — исследование физического явления в условиях, находящихся под контролем исследователя. В своей основе физика является экспериментальной наукой: большинство ее законов основаны на фактах, установленных опытным путем. | Анализ данных, полученных в результате экспериментов, формулирование законов природы, объяснение конкретных явлений и свойств на основе этих законов, а главное — предвидение и теоретическое обоснование (с широким использованием математики) еще не известных явлений и свойств. |
Какие наблюдения, теоретические и экспериментальные исследования вы провели бы, чтобы исследовать свечение обычной лампы накаливания?
Теоретические исследования проводят не с конкретным физическим телом, а с его идеализированным аналогом — физической моделью, которая должна учитывать только некоторые основные свойства исследуемого тела. Так, изучая движение автомобиля, мы иногда используем его физическую модель — материальную точку (рис. 2.1, а).
Эту модель используют, если размеры тела не существенны для теоретического описания, то есть в модели «материальная точка» учитывается только масса тела, а его форма и размеры во внимание не принимаются. А вот если нужно выяснить, как на движение автомобиля влияет сопротивление воздуха, целесообразно применить уже другую физическую модель — она должна учитывать и форму, и размеры автомобиля (рис. 2.1, б), но может не учитывать, например, размещение пассажиров в салоне. Чем больше выбрано соответствующих параметров для исследования физической системы «автомобиль», тем точнее можно предвидеть «поведение» этой системы.
Рис. 2.1. Определяя скорость и время движения автомобиля, можно применять физическую модель «материальная точка» (а); выясняя аэродинамические свойства автомобиля, эту физическую модель применять нельзя (б)
Целесообразно ли использовать физическую модель «материальная точка», если инженеры должны рассчитать устойчивость автомобиля?
Как измерить физическую величину
Описывая, например, движение автомобиля, мы используем определенные количественные характеристики: скорость, ускорение, время движения, силу тяги, мощность и т. п.
Из предыдущего курса физики вы знаете, что количественную меру свойства тела, физического процесса или явления называют физической величиной. Значение физической величины устанавливают в ходе измерений, которые, в свою очередь, бывают прямые и косвенные. При прямых измерениях величину сравнивают с ее единицей (метром, секундой, килограммом, ампером и т. п.) с помощью измерительного прибора, проградуированного в соответствующих единицах (рис. 2.2).
Рис. 2.2. Современные приборы для прямого измерения температуры (а); массы (б); скорости движения (в)
Назовите несколько физических величин, значения которых вы находили с помощью прямых измерений. В каких единицах измеряют эти величины? какими приборами? При косвенных измерениях величину вычисляют по результатам прямых измерений других величин, связанных с измеряемой величиной некоторой функциональной зависимостью. Так, чтобы найти среднюю плотность ρ тела, нужно с помощью весов измерить массу m тела, с помощью, например, мензурки измерить его объем V, а затем массу разделить на объем:
Построение системы единиц
В конце XVIII в., после Великой французской революции, перед французскими учеными была поставлена задача создать систему единиц на научной основе. В результате появилась метрическая система единиц. В 1960 г. была создана Международная система единиц CИ, которая со временем стала в мире доминирующей.
Основные единицы СИ
- килограмм (1 кг, 1 kg) единица массы
- метр (1 м, 1 m) единица длины
- секунда (1 с, 1 s) единица времени
- ампер (1 А, 1 А) единица силы тока
- моль (1 моль, 1 mol) единица количества вещества
- кельвин (1 К, 1 K) единица температуры
- кандела (1 кд, 1 kd) единица силы света
Исторически единицы физических величин связывали с определенными телами или природными процессами. Так, 1 метр был связан с размерами планеты Земля, 1 килограмм — с определенным объемом воды, 1 секунда — с суточным вращением Земли. Позже для каждой единицы был создан эталон — средство (или комплекс средств) для воспроизведения и хранения единицы физической величины. Основные эталоны хранились (и хранятся сейчас) в Международном бюро мер и весов (г. Севр, Франция).
Сейчас все большее распространение получают методы построения системы единиц, основанные на особенностях излучения и распространения электромагнитных волн, а также на фундаментальных физических константах. Рассмотрим основные этапы создания системы единиц на примерах метра и килограмма.
Напомним, что для удобства записи больших и малых значений физических величин используют кратные и дольные единицы. Кратные единицы больше основных единиц в 10, 100, 1000 и более раз. Дольные единицы меньше основных единиц в 10, 100, 1000 и более раз.
Названия кратных и дольных единиц включают в себя специальные префиксы. Например, километр (1000 м, или 103 м) — кратная единица длины, миллиметр (0,001 м, или 10–3 м) — дольная единица длины (см. табл. 1).
Таблица 1. Префиксы для образования названий кратных и дольных единиц
| Префикс | Символ | Множитель |
| атто- | а | 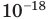 |
| фемто- | ф | 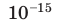 |
| пико- | п | 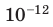 |
| нано- | н | 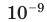 |
| микро- | мк | 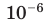 |
| милли- | м | 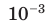 |
| санти- | с | 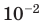 |
| кило- | к | 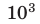 |
| мега- | М | 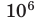 |
| гига- | Г | 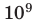 |
| тера- | Т | 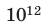 |
| пета | п | 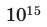 |
| экса | е | 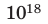 |
Погрешности измерений
При измерении любой физической величины обычно выполняют три последовательные операции: 1) выбор, проверка и установка прибора (приборов); 2) снятие показаний прибора (приборов); 3) вычисление искомой величины по результатам измерений (при косвенных измерениях); 4) оценка погрешности.
Например, нужно измерить на местности расстояние около 5 м. Разумеется, что для этого не следует брать ученическую линейку, — удобнее воспользоваться рулеткой. Все приборы имеют определенную точность. Расстояние в 5 м, как правило, не требуется определять с точностью до миллиметра, поэтому шкала рулетки может и не содержать соответствующих делений.
Рис. 2.3. Штангенциркуль. Точность измерения изображенным прибором — сотые доли миллиметра
А вот если для ремонта лабораторного крана необходимо определить размер шайбы, целесообразно воспользоваться штангенциркулем (см. рис. 2.3). Однако даже с помощью сверхточного прибора нельзя выполнить измерения абсолютно точно. Всегда есть погрешности измерений — отклонение значения измеренной величины от ее истинного значения. Модуль разности между измеренным (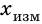
Отношение абсолютной погрешности к измеренному значению измеряемой величины называют относительной погрешностью измерения 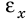
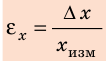
Погрешности при измерениях бывают случайные и систематические.
Случайные погрешности
Случайные погрешности связаны с процессом измерения: измеряя расстояние рулеткой, невозможно проложить ее идеально ровно; отсчитывая секундомером время, прибор невозможно мгновенно включить и выключить и т. д. Чтобы результаты были более точными, измерения проводят несколько раз и определяют среднее значение измеряемой величины:
где 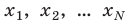
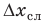
Если измерение проводилось один раз, будем считать, что случайная погрешность равна половине цены деления шкалы прибора.
Систематические погрешности
Систематические погрешности связаны прежде всего с выбором прибора: невозможно найти рулетку с идеально точной шкалой, идеально равноплечие рычаги и т. п. Систематические погрешности определяются классом точности прибора, поэтому их часто называют погрешностями прибора. В процессе эксплуатации точность приборов может снижаться, поэтому их необходимо периодически калибровать при помощи специального оборудования. Абсолютные погрешности некоторых приборов, используемых в школе, приведены в табл. 2. Если используются другие приборы, будем считать, что абсолютная погрешность прибора равна половине цены деления его шкалы.
Абсолютная погрешность прямого измерения (∆x) учитывает как систематическую погрешность, связанную с прибором (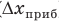
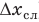
Обратите внимание! Приведенные формулы очень упрощены. Ученые используют более сложные методы расчетов погрешностей.
Таблица 2. Абсолютные погрешности некоторых физических приборов
| Физический прибор | Цена деления шкалы прибора | Абсолютная погрешность прибора |
| Линейка ученическая | 1 мм | ±1 мм |
| Лента измерительная | 0,5 см | ±0,5 см |
| Штангенциркуль | 0,1 мм | ±0,05 мм |
| Цилиндр измерительный | 1 мл | ±1 мл |
| Секундомер | 0,2 с | ±1 с за 30 мин |
| Динамометр учебный | 0,1 Н | ±0,05 Н |
| Термометр лабораторный | 1 °С | ±1 °С |
Как определить погрешности косвенных измерений
Многие физические величины невозможно измерить непосредственно. Их косвенное измерение включает два этапа: 1) методом прямых измерений находят значения определенных величин, например x, y; 2) по соответствующей формуле вычисляют искомую величину f. Как в таком случае определить абсолютную ∆f и относительную 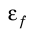
- Относительную погрешность определяют по специальным формулам (см. табл. 3).
- Абсолютную погрешность определяют по относительной погрешности:
- Если эксперимент проводят, чтобы выяснить, выполняется ли некое равенство (например, X Y= ), то относительную погрешность экспериментальной проверки равенства X Y= можно оценить по формуле:
Таблица 3. Некоторые формулы для определения относительной погрешности
| Функциональная зависимость | Относительная погрешность |
|---|---|
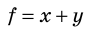 |
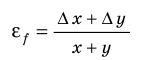 |
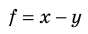 |
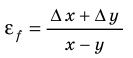 |
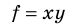 |
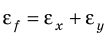 |
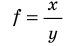 |
|
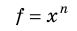 |
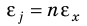 |
Как правильно записать результаты
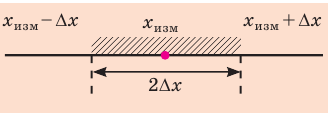
Абсолютная погрешность эксперимента определяет точность, с которой имеет смысл вычислять измеряемую величину. Абсолютную погрешность ∆x обычно округляют до одной значащей цифры с завышением, а результат измерения xизм — до величины разряда, оставшегося после округления в абсолютной погрешности. Окончательный результат х записывают в виде:
Абсолютная погрешность — положительная величина, поэтому 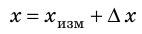
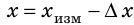
Рис. 2.4. Абсолютная погрешность измерения определяет интервал, в котором находится истинное значение измеряемой величины
Пример. Пусть измеряли ускорение свободного падения (g). После обработки экспериментальных данных получили: 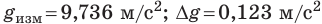
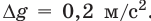
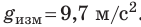
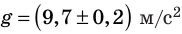
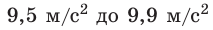
Рис. 2.5. Табличное значение: 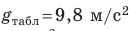
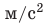
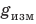
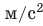
- Точность измерений и погрешности
- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Что изучает физика
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс
Со времен возникновения различных наук и математических расчетов ученые начали использовать множество символов и сокращений. Это вполне оправданное решение, ведь длинные формулы, записанные при помощи слов, отнимали бы много времени. По какому принципу выбираются эти обозначения, в частности буквы, указывающие на скорость и расстояние?
Как обозначают физические величины и понятия?
В физике существует общепринятый список обозначений. Он включает латинские и греческие буквы, кириллицу (редко), специальные символы, надстрочные и подстрочные знаки, скобки и др. В качестве самостоятельной науки физика зародилась в 17-м веке во время научной революции, но многие идеи, физические воззрения появились еще в античный период. Отсюда и использование латыни, греческого языка.
Количество физических величин довольно большое – букв в алфавитах недостаточно для обозначения их всех. Поэтому одни и те же буквы могут обозначать разные понятия. Важно различать и стиль написания.
Например, латинские символы обычно пишутся курсивом, греческие – обыкновенным прямым начертанием. Строчными буквами обозначают интенсивные величины (не зависят от размеров системы, например, температура), заглавными – экстенсивные.
Интересный факт: среди всех латинских букв для обозначения понятий из области физики реже всего встречается буква о.
Ввиду исторических причин множество обозначений с использованием латинских букв – это сокращения слов, которые указывают на данные понятия. Чаще всего это латинские, английские, немецкие и французские слова. Во избежание путаницы почти не используются греческие заглавные буквы, если они похожи на латинские по манере написания.
Почему в физике расстояние обозначается буквой s?
Расстояние в физике измеряется единицами длины (метр в международной системе единиц) и имеет два значения:
- степень удаленности объектов друг от друга;
- длина пути, которую прошел объект.
Расстояние – один из тех случаев, когда обозначающая буква является первой в слове-определении. Некоторые источники по-разному объясняют происхождение буквы s:
- От английского слова «space», которое означает расстояние, пространство, площадь.
- От латинского «spatium» – пространство между двумя предметами, протяжение в длину и ширину.
Фактически оба варианта являются правильными. Согласно этимологии слова «space», оно вошло в употребление в 1300-х годах и происходит от французского «espace», а оно, в свою очередь, от латинского «spatium». В значении космического пространства «space» начало употребляться лишь с конца 17-го века, после того как появилось в художественном произведении Джона Мильтона.
Почему в физике скорость обозначается буквой v?
Для обозначения скорости в физике используют строчную букву v тоже не случайно. Это первая буква в латинском слове «velocitas», французском «vitesse» и английском «velocity». Все они означают скорость, быстроту, стремительность.
Возникает другой вопрос: почему именно «velocity» стало определением скорости, а не другие английские слова с похожим значением, например, «speed»? Дело в том, что в физике скорость является векторной величиной, которая отображает быстроту и направление перемещения объекта относительно заданной системы отсчета.
Слово «speed» указывает на скалярную скорость – величину, которая не зависит от системы координат. Например, скорость света – постоянная величина, поэтому на английском данный термин будет выглядеть как «the speed of light».
Кроме того, скорость и расстояние – взаимосвязанные величины наряду со временем. Эта связь в физике выражается формулой. Зная две величины, можно рассчитать и третью. Использование одинаковых букв нецелесообразно.
Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Единицы физических величин (единицы измерения), метрические системы, соотношения и переводы единиц измерения
Единицы физических величин. Общая информация
Единица физической величины (единица величины, единица, единица измерения) (англ. Measurement unit, unit of measurement, unit) — физическая величина фиксированного размера, которой условно по соглашению присвоено числовое значение, равное 1.
С единицей физической величины можно сравнить любую другую величину того же рода и выразить их отношение в виде числа. Применяется для количественного выражения однородных с ней физических величин.
Единицы измерения имеют присвоенные им по соглашению наименования и обозначения.
Различают основные и производные единицы.
Основные единицы в данной системе единиц устанавливаются для тех физических величин, которые выбраны в качестве основных в соответствующей системе физических величин. Так, Международная система единиц (СИ) основана на Международной системе величин (англ. International System of Quantities, ISQ), в которой основными являются семь величин: длина, масса, время, электрический ток, термодинамическая температура, количество вещества и сила света.
Соответственно, в СИ основными единицами являются единицы указанных величин.
Размеры основных единиц устанавливаются по соглашению в рамках соответствующей системы единиц и фиксируются либо с помощью эталонов (прототипов), либо путём фиксации численных значений фундаментальных физических постоянных.
Производные единицы определяются через основные путём использования тех связей между физическими величинами, которые установлены в системе физических величин.
Существует большое количество различных систем единиц, которые различаются как системами величин, на которых они основаны, так и выбором основных единиц.
Государство, как правило, законодательно устанавливает какую-либо систему единиц в качестве предпочтительной или обязательной для использования в стране.
Соотношение единиц измерения
|
Меры длины |
Меры площади |
|
Меры объема |
Меры веса |
|
Меры времени |
Меры давления |
|
Меры тока |
Меры напряжения и э.д.с. |
|
Меры мощности |
Меры сопротивления |
|
Меры частоты |
Меры количества информации 1 байт = 8 бит |
Для единиц измерения информации степени двойки (210, 220 и т.д.) являются точными значениями килобайт, мегабайт, гигабайт. А степени числа 10 (103, 106 и т.п.) — приблизительные значения, округленные в сторону уменьшения.
Такое приближение (или округление) вполне допустимо и является общепринятым
Системы единиц измерения
Метрические системы
Метрическая система — общее название международной десятичной системы единиц, основанной на использовании метра и килограмма.
На протяжении двух последних веков существовали различные варианты метрической системы, различающиеся выбором основных единиц.
В настоящее время повсеместно признанной является Международная система единиц (СИ).
Метрическая система официально принята во всех государствах мира, кроме США, Либерии и Мьянмы (Бирма).
НУЖЕН АНГЛИЙСКИЙ?
6 лучших онлайн-школ и сервисов
Инглекс
englex.ru
обучение английскому языку по скайпу- живое общение с преподавателем
Skyeng
skyeng.ru
одна из крупнейших онлайн школ английского для аудитории СНГ
Фоксфорд
foxford.ru
эффективные курсы с погружением в англоязычную среду
Skillbox
eng.skillbox.ru
все программы английского языка
Puzzle English
puzzle-english.com
популярный онлайн-сервис для изучения английского языка
Lingualeo
lingualeo.com/ru
эффективный сервис для увлекательной практики языков
Основное отличие метрической системы от применявшихся ранее традиционных систем заключается в использовании упорядоченного набора единиц измерения. Для любой физической величины существует лишь одна главная единица и набор дольных и кратных единиц, образуемых стандартным образом с помощью десятичных приставок.
Тем самым устраняется неудобство от использования большого количества разных единиц (таких, например, как дюймы, футы, фадены, мили и т. д.) со сложными правилами преобразования между ними. В метрической системе преобразование сводится к умножению или делению на степень числа 10, то есть к простой перестановке запятой в десятичной дроби.
Основная используемая система
СИ
Неиспользуемые или малоиспользуемые системы
СГС
МКС
МКГСС
МТС
МСК
МКСЛ
Системы естественных единиц измерения
Атомная система единиц
Планковские единицы
Геометризованная система единиц
Единицы Лоренца — Хевисайда
Традиционные системы мер
Русская система мер
Английская система мер
Французская система мер
Китайская система мер
Японская система мер
Давно устаревшие (древнегреческая, древнеримская, древнеегипетская, древневавилонская, древнееврейская)
Международная система единиц СИ
Международная система единиц СИ (фр. Système international d’unités, SI) — система единиц физических величин, современный вариант метрической системы.
СИ принята в качестве основной системы единиц большинством стран мира и почти всегда используется в области техники, даже в тех странах, в которых в повседневной жизни используются традиционные единицы.
В этих немногих странах (например, в США) определения традиционных единиц были изменены таким образом, чтобы связать их фиксированными коэффициентами с соответствующими единицами СИ.
Полное официальное описание СИ вместе с её толкованием содержится в действующей редакции Брошюры СИ (фр. Brochure SI, англ. The SI Brochure) и в дополнении к ней, опубликованных Международным бюро мер и весов (МБМВ) и представленных на сайте МБМВ — bipm.org
Брошюра СИ издаётся с 1970 года, с 1985 года выходит на французском и английском языках, переведена также на ряд других языков, однако официальным считается текст только на французском языке.
Основные единицы СИ
|
Величина |
Единица |
||||
|
Наименование |
Символ |
Наименование |
Обозначение |
||
|
русское |
французское/ |
русское |
между |
||
|
Длина |
L |
метр |
mètre/metre |
м |
m |
|
Масса |
M |
килограмм |
kilogramme/kilogram |
кг |
kg |
|
Время |
T |
секунда |
seconde/second |
с |
s |
|
Сила электрического тока |
I |
ампер |
ampère/ampere |
А |
A |
|
Термодинамическая температура |
Θ |
кельвин |
kelvin |
К |
K |
|
Количество вещества |
N |
моль |
mole |
моль |
mol |
|
Сила света |
J |
кандела |
candela |
кд |
cd |
Наименования единиц СИ пишутся со строчной буквы, после обозначений единиц СИ точка не ставится, в отличие от обычных сокращений.
У этого правила есть исключение: обозначения единиц, названных фамилиями учёных, пишутся с заглавной буквы (например, ампер обозначается символом А).
Производные единицы
Остальные единицы СИ являются производными и образуются из основных с помощью уравнений, связывающих друг с другом физические величины используемой в СИ Международной системы величин.
Основная единица может использоваться и для производной величины той же размерности. Например, количество осадков определяется как частное от деления объёма на площадь и в СИ выражается в метрах. В этом случае метр используется в качестве когерентной производной единицы.
Определение СИ через фиксацию констант, в принципе не требует различать основные и производные единицы. Тем не менее, это разделение сохраняется по историческим причинам и для удобства.
Примеры производных единиц СИ, наименования и обозначения которых образованы с использованием наименований и обозначений основных единиц СИ
|
Величина |
Единица |
||
|
Наименование |
Наименование |
Обозначение |
|
|
между |
русское |
||
|
Площадь |
квадратный метр |
m |
м |
|
Объем, вместимость |
кубический метр |
m |
м |
|
Скорость |
метр в секунду |
m/s |
м/с |
|
Ускорение |
метр на секунду в квадрате |
m/s |
м/с |
|
Волновое число |
метр в минус первой степени |
m |
м |
|
Плотность |
килограмм на кубический метр |
kg/m |
кг/м |
|
Удельный объем |
кубический метр на килограмм |
m/kg |
м/кг |
|
Плотность электрического тока |
ампер на квадратный метр |
А/m |
А/м |
|
Напряженность магнитного поля |
ампер на метр |
А/m |
А/м |
|
Молярная концентрация компонента |
моль на кубический метр |
mol/m |
моль/м |
|
Яркость |
кандела на квадратный метр |
cd/m |
кд/м |
Производные единицы, имеющие специальные наименования и обозначения
Производные единицы могут быть выражены через основные с помощью математических операций — умножения и деления. Некоторым из производных единиц для удобства присвоены собственные наименования, такие единицы тоже можно использовать в математических выражениях для образования других производных единиц.
|
Величина |
Единица измерения |
Обозначение |
Выражение через |
||
|
русское |
международное |
русское |
между |
||
|
Плоский угол |
радиан |
radian |
рад |
rad |
м·м−1 = 1 |
|
Телесный угол |
стерадиан |
steradian |
ср |
sr |
м2·м−2 = 1 |
|
Температура по шкале Цельсия |
градус Цельсия |
degree Celsius |
°C |
°C |
K |
|
Частота |
герц |
hertz |
Гц |
Hz |
с−1 |
|
Сила |
ньютон |
newton |
Н |
N |
кг·м·c−2 |
|
Энергия |
джоуль |
joule |
Дж |
J |
Н·м = кг·м2·c−2 |
|
Мощность |
ватт |
watt |
Вт |
W |
Дж/с = кг·м2·c−3 |
|
Давление |
паскаль |
pascal |
Па |
Pa |
Н/м2 = кг·м−1·с−2 |
|
Световой поток |
люмен |
lumen |
лм |
lm |
кд·ср |
|
Освещённость |
люкс |
lux |
лк |
lx |
лм/м² = кд·ср/м² |
|
Электрический заряд |
кулон |
coulomb |
Кл |
C |
А·с |
|
Разность потенциалов |
вольт |
volt |
В |
V |
Дж/Кл = кг·м2·с−3·А−1 |
|
Сопротивление |
ом |
ohm |
Ом |
Ω |
В/А = кг·м2·с−3·А−2 |
|
Электроёмкость |
фарад |
farad |
Ф |
F |
Кл/В = с4·А2·кг−1·м−2 |
|
Магнитный поток |
вебер |
weber |
Вб |
Wb |
кг·м2·с−2·А−1 |
|
Магнитная индукция |
тесла |
tesla |
Тл |
T |
Вб/м2 = кг·с−2·А−1 |
|
Индуктивность |
генри |
henry |
Гн |
H |
кг·м2·с−2·А−2 |
|
Электрическая проводимость |
сименс |
siemens |
См |
S |
Ом−1 = с3·А2·кг−1·м−2 |
|
Активность (радиоактивного источника) |
беккерель |
becquerel |
Бк |
Bq |
с−1 |
|
Поглощённая доза |
грей |
gray |
Гр |
Gy |
Дж/кг = м²/c² |
|
Эффективная доза |
зиверт |
sievert |
Зв |
Sv |
Дж/кг = м²/c² |
|
Активность катализатора |
катал |
katal |
кат |
kat |
моль/с |
Существуют другие внесистемные единицы, такие как литр, которые не являются единицами СИ, но принимаются для использования вместе с СИ.
Единицы измерения по измеряемым величинам. Википедия
ru.wikipedia.org/wiki
Единицы измерения по отраслям науки. Википедия
- Единицы измерения в астрономии
- Единицы измерения в информатике
- Единицы измерения в медицине
- Единицы измерения в физике
- Единицы измерения в химии
Приставки СИ
Приставки СИ (десятичные приставки) — приставки перед названиями или обозначениями единиц измерения физических величин, применяемые для формирования кратных и дольных единиц, отличающихся от базовой в определённое целое, являющееся степенью числа 10, число раз.
Десятичные приставки служат для сокращения количества нулей в численных значениях физических величин.
Рекомендуемые для использования приставки и их обозначения установлены Международной системой единиц (СИ), однако их использование не ограничено СИ, а многие из них восходят к моменту появления метрической системы (1790-е годы).
Приставки для кратных единиц
Кратные единицы — единицы, которые в целое число раз (10 в какой-либо степени) превышают основную единицу измерения некоторой физической величины. Международная система единиц (СИ) рекомендует следующие десятичные приставки для обозначений кратных единиц:
|
Десятичный множитель |
Приставка |
Обозначение |
Пример |
||
|
русская |
между |
русское |
между |
||
|
101 |
дека |
deca |
да |
da |
дал — декалитр |
|
102 |
гекто |
hecto |
г |
h |
гПа — гектопаскаль |
|
103 |
кило |
kilo |
к |
k |
кН — килоньютон |
|
106 |
мега |
mega |
М |
M |
МПа — мегапаскаль |
|
109 |
гига |
giga |
Г |
G |
ГГц — гигагерц |
|
1012 |
тера |
tera |
Т |
T |
ТВ — теравольт |
|
1015 |
пета |
peta |
П |
P |
Пфлопс — петафлопс |
|
1018 |
экса |
exa |
Э |
E |
Эм — эксаметр |
|
1021 |
зетта |
zetta |
З |
Z |
ЗэВ — зеттаэлектронвольт |
|
1024 |
иотта |
yotta |
И |
Y |
Иг — иоттаграмм |
Приставки для дольных единиц
Дольные единицы составляют определённую долю (часть) от установленной единицы измерения некоторой величины.
Международная система единиц (СИ) рекомендует следующие приставки для обозначений дольных единиц:
|
Десятичный множитель |
Приставка |
Обозначение |
Пример |
||
|
русская |
между |
русское |
между |
||
|
10−1 |
деци |
deci |
д |
d |
дм — дециметр |
|
10−2 |
санти |
centi |
с |
c |
см — сантиметр |
|
10−3 |
милли |
milli |
м |
m |
мH — миллиньютон |
|
10−6 |
микро |
micro |
мк |
µ |
мкм — микрометр |
|
10−9 |
нано |
nano |
н |
n |
нм — нанометр |
|
10−12 |
пико |
pico |
п |
p |
пФ — пикофарад |
|
10−15 |
фемто |
femto |
ф |
f |
фл — фемтолитр |
|
10−18 |
атто |
atto |
а |
a |
ас — аттосекунда |
|
10−21 |
зепто |
zepto |
з |
z |
зКл — зептокулон |
|
10−24 |
иокто |
yocto |
и |
y |
иг — иоктограмм |
Семь основных единиц измерения (СИ)+площадь и объем
Базовые единицы СИ. Международное бюро мер и весов — bipm.org/en/measurement-units
1
Единицы измерения массы (масса)
В настоящее время в Международной системе единиц (СИ) в качестве единицы измерения массы принят килограмм, являющийся одной из семи основных единиц СИ.
XXVI Генеральная конференция по мерам и весам c 20 мая 2019г. одобрила новое определение килограмма, основанное на фиксации численного значения постоянной Планка
Теперь килограмм измеряется не весом эталонного цилиндра, а энергией, необходимой для того, чтобы сдвинуть этот килограмм.
Тонна — 106 (1 000 000) граммов, или 1000 килограммов.
Центнер — 105 (100 000) граммов, или 100 килограммов.
Карат — 0,2 грамма.
Единицы массы в науке
Атомная единица массы (а. е. м., дальтон) = 1,660 538 921(73)⋅10−27 кг = 1,660 538 921(73)⋅10−24 г (в химии высокомолекулярных соединений и биохимии применяются также кратные единицы килодальтон, мегадальтон).
Солнечная масса M☉ = 1.98847(7)⋅1030 кг.
Электронвольт, 1 эВ = 1,782 661 845(39)⋅10−36 кг; применяются также кратные (килоэлектронвольт, кэВ; мегаэлектронвольт, МэВ, гигаэлектронвольт, ГэВ; тераэлектронвольт, ТэВ) и дольные (миллиэлектронвольт, мэВ) единицы.
Масса электрона me = 9,109 382 91(40)⋅10−31 кг.
Масса протона mp = 1,672 621 777(74)⋅10−27 кг.
Планковская единица массы MPl = 2,176 51(13)⋅10−8 кг.
2
Единицы измерения расстояния (расстояние)
Единицей измерения расстояния и одной из основных единиц в Международной системе единиц (СИ) является метр.
На практике применяются также кратные и дольные единицы метра, образуемые с помощью стандартных приставок СИ:
|
Кратные |
Дольные |
||||||
|
величина |
название |
обозначение |
величина |
название |
обозначение |
||
|
101 м |
декаметр |
дам |
dam |
10−1 м |
дециметр |
дм |
dm |
|
102 м |
гектометр |
гм |
hm |
10−2 м |
сантиметр |
см |
cm |
|
103 м |
километр |
км |
km |
10−3 м |
миллиметр |
мм |
mm |
|
106 м |
мегаметр |
Мм |
Mm |
10−6 м |
микрометр |
мкм |
µm |
|
109 м |
гигаметр |
Гм |
Gm |
10−9 м |
нанометр |
нм |
nm |
|
1012 м |
тераметр |
Тм |
Tm |
10−12 м |
пикометр |
пм |
pm |
|
1015 м |
петаметр |
Пм |
Pm |
10−15 м |
фемтометр |
фм |
fm |
|
1018 м |
эксаметр |
Эм |
Em |
10−18 м |
аттометр |
ам |
am |
|
1021 м |
зеттаметр |
Зм |
Zm |
10−21 м |
зептометр |
зм |
zm |
|
1024 м |
иоттаметр |
Им |
Ym |
10−24 м |
иоктометр |
им |
ym |
Единицы, применяемые в астрономии
- радиус Луны (R☾) = 1737,10 км;
- радиус Земли (R⊕) = 6371,0 км;
- радиус Юпитера(R♃или RJ) = 69 911 км;
- световая секунда = 299 792 458 м ;
- радиус Солнца (R⊙) = 6,9551⋅105км;
- световой месяц = 783934206048416.66… м
- астрономическая единица = 149 597 870,700 км;
- спат (единица длины)(англ.)= 1⋅1012 м;
- световой год = 9 460 730 472 581 000 м ;
- парсек= (648 000/π) а.е. (точно) ≈ 206264,806247 а.е. = 3,08567758491⋅1016м;
- сириометр = 106а.е. = 149 597 870 700 000 000 м;
Единицы, применяемые в физике
- планковская длина ≈ 1,616199(97)⋅10−35м;
- ферми = 1 фм = 1⋅10−15м;
- классический радиус электрона = 2,8179402894(58)⋅10−15м;
- икс-единица = 1,00207⋅10−13м;
- комптоновская длина волны электрона= 2,4263102175(33)⋅10−12м;
- боровский радиус = 5,2917720859(36)⋅10−11м;
- ангстрем = 1⋅10−10м;
Единицы измерения площади (площадь)
Квадратный метр (русское обозначение: м², международное: m²) — единица измерения площади в Международной системе единиц (СИ), а также в системах МТС и МКГСС.
1 м² равен площади квадрата со стороной в 1 метр.
1 м² = 1 са (сантиар);
Квадратный километр, 1 км² = 1 000 000 м²;
Гектар, 1 га = 10 000 м²;
Ар (сотка), 1 а = 100 м²:
Квадратный дециметр, 100 дм² = 1 м²;
Квадратный сантиметр, 10 000 см² = 1 м²;
Квадратный миллиметр, 1 000 000 мм² = 1 м²;
Барн, 1 б = 10−28 м².
Единицы измерения объёма (объём)
Объём — количественная характеристика пространства, занимаемого телом или веществом.
Кубический метр (кубометр) — единица объёма, производная в Международной системе единиц (СИ), а также в системах единиц МКГСС и МТС.
Одному кубическому метру равен объём куба с длиной ребра 1 метр.
От неё образуются производные единицы — кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма — галлон, баррель и др.
В формулах для обозначения объёма традиционно используется заглавная латинская буква V, являющаяся сокращением от лат. volume — «объём», «наполнение».
Единицы объёма жидкости
1 литр = 1 кубический дециметр = 1,76 пинты = 0,23 галлона
Русские
Ведро = 12,3 литра
Бочка = 40 вёдер = 492 литра
Английские
1 пинта = 0,568 литра
1 кварта (жидкостная) = 2 пинтам = 1,136 литра
1 галлон = 8 пинтам = 4,55 литра
1 галлон (амер.) = 3,785 литра
3
Единицы измерения температуры (температура)
Существует несколько различных единиц измерения температуры. Они делятся на относительные (градус Цельсия, градус Фаренгейта…) и абсолютные (Кельвин, градус Ранкина…).
Наиболее известными являются следующие:
Градус Цельсия (°C)
Градус Фаренгейта (°F)
Кельвин (K)
Градус Реомюра (°Ré, °Re, °R)
Градус Рёмера (°Rø)
Градус Ранкина (°Ra)
Градус Делиля (°Д или °D)
Градус Гука (°H)
Градус Дальтона (°Dа)
Градус Ньютона (°N)
Лейденский градус (°L или ÐL)
Планковская температура (TP)
Кельвин (русское обозначение: К; международное: K) — единица термодинамической температуры в Международной системе единиц (СИ), одна из семи основных единиц СИ. Определяется через значение постоянной Больцмана: 1,380649 × 10-23 Дж / К. Начало шкалы (0 К) совпадает с абсолютным нулём.
Градус Цельсия (обозначение: °C) —единица температуры, применяемая в Международной системе единиц (СИ) наряду с кельвином.
Используется всеми странами, кроме США, Багамских Островов, Белиза, Каймановых Островов и Либерии.
Согласно современному определению, один градус Цельсия равен одному кельвину (K), а ноль шкалы Цельсия установлен таким образом, что температура тройной точки воды равна 0,01 °C. В итоге шкалы Цельсия и Кельвина сдвинуты на 273,15 единиц:
Пересчёт в градусы Цельсия:
t_{C}=t_{K}-273,15}t_{C}=t_{K}-273,15 (температура тройной точки воды +0,01 °C).
Основные международные и российские документы, содержащие описание единиц СИ и регламентирующие их использование, называют градус Цельсия не единицей температуры, а единицей температуры Цельсия (фр. température Celsius, англ. Celsius temperature). Этот термин используется в Брошюре СИ (фр. Brochure SI, англ. The SI Brochure), опубликованной Международным бюро мер и весов (МБМВ)
В свою очередь температуру Цельсия (обозначение t) Брошюра СИ и ГОСТ 8.417-2002 определяют выражением t = T — T0, где T — термодинамическая температура, выражаемая в кельвинах, а T0 = 273,15 К.
В соответствии со сказанным градус Цельсия относится к производным единицам СИ, имеющим специальные наименования и обозначения.
Пересчёт температуры между основными шкалами
|
Шкала |
Условное |
из Цельсия (°C) |
в Цельсий |
|
Фаренгейт |
(°F) |
[°F] = [°C] × 9⁄5 + 32 |
[°C] = ([°F] − 32) × 5⁄9 |
|
Кельвин |
(K) |
[K] = [°C] + 273,15 |
[°C] = [K] − 273,15 |
|
Ранкин (Rankin) |
(°R) |
[°R] = ([°C] + 273,15) × 9⁄5 |
[°C] = ([°R] − 491,67) × 5⁄9 |
|
Делиль (Delisle) |
(°Д или °De) |
[°De] = (100 − [°C]) × 3⁄2 |
[°C] = 100 − [°De] × 2⁄3 |
|
Ньютон (Newton) |
(°N) |
[°N] = [°C] × 33⁄100 |
[°C] = [°N] × 100⁄33 |
|
Реомюр (Réaumur) |
(°Re, °Ré, °R) |
[°Ré] = [°C] × 4⁄5 |
[°C] = [°Ré] × 5⁄4 |
|
Рёмер (Rømer) |
(°Rø) |
[°Rø] = [°C] × 21⁄40 + 7,5 |
[°C] = ([°Rø] − 7,5) × 40⁄21 |
Сравнение температурных шкал
|
Описание |
Кельвин |
Цельсий |
Фаренгейт |
|
Абсолютный нуль |
0 |
−273,15 |
−459,67 |
|
Температура таяния смеси Фаренгейта (соль,лёд и хлорид аммония) |
255,37 |
−17,78 |
0 |
|
Температура замерзания воды (Нормальные условия) |
273,15 |
0 |
32 |
|
Средняя температура человеческого тела |
309,75 |
36,6 |
98,2 |
|
Температура кипения воды (Нормальные условия) |
373,15 |
100 |
212 |
|
Плавление титана |
1941 |
1668 |
3034 |
|
Солнце |
5800 |
5526 |
9980 |
4
Единицы измерения времени (время)
Современные единицы измерения времени основаны на периодах вращения Земли вокруг своей оси и обращения вокруг Солнца, а также обращения Луны вокруг Земли. Такой выбор единиц обусловлен как историческими, так и практическими соображениями: необходимостью согласовывать деятельность людей со сменой дня и ночи или сезонов.
Исторически основной единицей для измерения средних интервалов времени были сутки (часто говорят «день»), отсчитываемые по минимальным полным циклам смены солнечной освещённости (день и ночь).
В результате деления суток на меньшие временны́е интервалы одинаковой длины возникли часы, минуты и секунды.
Сутки делили на два равных последовательных интервала (условно день и ночь). Каждый из них делили на 12 часов. Дальнейшее деление часа восходит к шестидесятеричной системе счисления. Каждый час делили на 60 минут. Каждую минуту — на 60 секунд.
Таким образом, в часе 3600 секунд; в сутках — 24 часа, или 1440 минут, или 86 400 секунд.
Секунда (русское обозначение: с; международное: s) — единица измерения времени, является одной из семи основных единиц в Международной системе единиц (СИ) и одной из трёх основных единиц в системе СГС.
Представляет собой интервал времени, равный 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133, находящегося в покое при 0 К.
В астрономии используют обозначения ч, м, с (или h, m, s) в верхнем индексе: например, 13ч20м10с (или 13h20m10s).
Кратные и дольные единицы
С единицей измерения «секунда», как правило, используются только дольные приставки СИ (кроме деци- и санти-). Для измерения больших интервалов времени используются единицы минута, час, сутки, и т. д.
|
Кратные |
Дольные |
||||||
|
величина |
название |
обозначение |
величина |
название |
обозначение |
||
|
101 с |
декасекунда |
дас |
das |
10−1 с |
децисекунда |
дс |
ds |
|
102 с |
гектосекунда |
гс |
hs |
10−2 с |
сантисекунда |
сс |
cs |
|
103 с |
килосекунда |
кс |
ks |
10−3 с |
миллисекунда |
мс |
ms |
|
106 с |
мегасекунда |
Мс |
Ms |
10−6 с |
микросекунда |
мкс |
µs |
|
109 с |
гигасекунда |
Гс |
Gs |
10−9 с |
наносекунда |
нс |
ns |
|
1012 с |
терасекунда |
Тс |
Ts |
10−12 с |
пикосекунда |
пс |
ps |
|
1015 с |
петасекунда |
Пс |
Ps |
10−15 с |
фемтосекунда |
фс |
fs |
|
1018 с |
эксасекунда |
Эс |
Es |
10−18 с |
аттосекунда |
ас |
as |
|
1021 с |
зеттасекунда |
Зс |
Zs |
10−21 с |
зептосекунда |
зс |
zs |
|
1024 с |
иоттасекунда |
Ис |
Ys |
10−24 с |
иоктосекунда |
ис |
ys |
Эквивалентность другим единицам измерения времени
1 секунда равна:
• 1/60 минуты
• 1/3 600 часа
• 1/86 400 суток (система единиц МАС)
• 1/31 557 600 юлианского года (система единиц МАС)
5
Сила электрического тока
Средняя сила тока I — физическая величина , равная отношению заряда, прошедшего через поперечное сечение проводника за промежуток времени, к величине этого промежутка времени: I=△q/△t
Если сила тока со временем не меняется, то ток называется постоянным.
Сила тока в данный момент времени определяется так же по этой формуле, но промежуток времени должен быть очень малым.
Обычно обозначается символом I, от фр. intensité du courant.
Сила тока в Международной системе единиц (СИ) измеряется в амперах ((русское обозначение: А; международное: A), ампер является одной из семи основных единиц СИ.
1 А = 1 Кл/с.
В амперах измеряется также магнитодвижущая сила и разность магнитных потенциалов (устаревшее наименование — ампер-виток). Кроме того, ампер является единицей силы тока и относится к числу основных единиц в системе единиц МКСА.
На XXVI Генеральной конференции мер и весов было принято новое определение ампера, основанное на использовании численного значения элементарного электрического заряда. Формулировка вступила в силу 20 мая 2019 года.
В соответствии с данной формулировкой, Ампер, символ А, есть единица электрического тока в СИ. Она определена путём фиксации численного значения элементарного заряда равным 1,602 176 634⋅10−19, когда он выражен единицей Кл, которая равна А·с, где секунда определена через .△νCs
△νCs — частота излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.
6
Количество вещества
Количество вещества́ — физическая величина, характеризующая количество однотипных структурных единиц, содержащихся в веществе. Под структурными единицами понимаются любые частицы, из которых состоит вещество (атомы, молекулы, ионы, электроны или любые другие частицы).
Моль (русское обозначение: моль; международное: mol; устаревшее название грамм-молекула (по отношению к количеству молекул); от лат. moles — количество, масса, счётное множество) — единица измерения количества вещества в Международной системе единиц (СИ), одна из семи основных единиц СИ.
Значение одного моля определяется через число Авогадро, один моль — количество вещества, содержащее 6,022 140 76⋅1023 частиц (атомов, молекул, ионов, электронов или любых других объектов).
6,022 140 76 x 10 23 элементарных сущностей. Это число представляет собой фиксированное числовое значение постоянной Авогадро, N A , выраженное в единицах моль –1, и называется числом Авогадро.
Количество вещества (символ n ) в системе является мерой количества определенных элементарных сущностей. Элементарным объектом может быть атом, молекула, ион, электрон, любая другая частица или определенная группа частиц.
Кратные и дольные единицы
Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ. Причём, единица измерения «иоктомоль» может использоваться лишь формально, так как столь малые количества вещества должны измеряться отдельными частицами (1 имоль формально равен 0,602 частицы).
|
Кратные |
Дольные |
||||||
|
величина |
название |
обозначение |
величина |
название |
обозначение |
||
|
101 моль |
декамоль |
дамоль |
damol |
10−1 моль |
децимоль |
дмоль |
dmol |
|
102 моль |
гектомоль |
гмоль |
hmol |
10−2 моль |
сантимоль |
смоль |
cmol |
|
103 моль |
киломоль |
кмоль |
kmol |
10−3 моль |
миллимоль |
ммоль |
mmol |
|
106 моль |
мегамоль |
Ммоль |
Mmol |
10−6 моль |
микромоль |
мкмоль |
µmol |
|
109 моль |
гигамоль |
Гмоль |
Gmol |
10−9 моль |
наномоль |
нмоль |
nmol |
|
1012 моль |
терамоль |
Тмоль |
Tmol |
10−12 моль |
пикомоль |
пмоль |
pmol |
|
1015 моль |
петамоль |
Пмоль |
Pmol |
10−15 моль |
фемтомоль |
фмоль |
fmol |
|
1018 моль |
эксамоль |
Эмоль |
Emol |
10−18 моль |
аттомоль |
амоль |
amol |
|
1021 моль |
зеттамоль |
Змоль |
Zmol |
10−21 моль |
зептомоль |
змоль |
zmol |
|
1024 моль |
иоттамоль |
Имоль |
Ymol |
10−24 моль |
иоктомоль |
имоль |
ymol |
Молярная масса — характеристика вещества, отношение массы вещества к количеству молей этого вещества, то есть масса одного моля вещества.
7
Сила света
Сила света Iν — физическая величина, одна из основных световых фотометрических величин. Характеризует величину световой энергии, переносимой в некотором направлении в единицу времени.
Количественно равна отношению светового потока, распространяющегося внутри элементарного телесного угла, к этому углу.
Понятие «сила света» возможно применять лишь для расстояний от источника света, существенно превышающих его линейные размеры.
Единица измерения в Международной системе единиц (СИ): кандела.
Канде́ла (от лат. candela — свеча; русское обозначение: кд; международное: cd) — единица силы света, одна из семи основных единиц Международной системы единиц (СИ).
Определена как «сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540⋅1012 Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср».
Принята в качестве единицы СИ в 1979 году XVI Генеральной конференцией по мерам и весам.
Из определения следует, что значение спектральной световой эффективности монохроматического излучения для частоты 540⋅1012 Гц равно 683 лм/Вт = 683 кд·ср/Вт точно.
Выбранная частота соответствует длине волны 555,016 нм в воздухе при стандартных условиях и находится вблизи максимума чувствительности человеческого глаза, располагающегося на длине волны 555 нм. Если излучение имеет другую длину волны, то для достижения той же силы света требуется бо́льшая энергетическая сила света.
Световые фотометрические величины СИ
ru.wikipedia.org
Преобразование единиц измерения.
Таблицы пересчета физических величин
Преобразование единиц — перевод физической величины, выраженной в одной системе единиц, в другую систему, обычно через коэффициент пересчёта.
ru.wikipedia.org
Длина
|
1 дюйм |
= 2,54 см |
1 миллиметр |
= 0,03937 дюйма |
|
1 фут |
= 0,3048 м |
1 сантиметр |
= 0,3937 дюйма |
|
1 ярд |
= 0,9144 м |
1 дециметр |
= 0,3281 фута |
|
1 род |
= 5,0292 м |
1 метр |
= 3,281 фута |
|
1 чейн |
= 20,117 м |
1 метр |
= 1,094 ярда |
|
1 фурлонг |
= 201,17 м |
1 декаметр |
= 10,94 ярда |
|
1 миля |
= 1,6093 м |
1 километр |
= 0,6214 мили |
|
1 морская миля |
= 1,8532 м |
1 километр |
= 0,539 морской мили |
Площадь
|
1 кв. дюйм |
= 6,4516 кв. см |
1 кв. сантиметр |
= 0,1550 кв. дюйма |
|
1 кв. фут |
= 929,03 кв. см |
1 кв. метр |
= 1,550 кв. дюйма |
|
1 кв. ярд |
= 0,8361 кв. м |
1 ар |
= 119,60 кв. ярда |
|
1 акр |
= 4046,9 кв. м |
1 гектар |
= 2,4711 акра |
|
1 кв. миля |
= 259,0 га |
1 кв. километр |
= 0,3861 кв. мили |
Объем
|
1 куб. дюйм |
= 16,387 куб. см |
1 куб. сантиметр |
= 0,061 куб. дюйма |
|
1 куб. фут |
= 0,0283 куб. м |
1 куб. дециметр |
= 0,035 куб. фута |
|
1 куб. ярд |
= 0,7646 куб. м |
1 куб. метр |
= 1,308 куб. ярда |
Меры сыпучих тел и жидкостей
|
Британия |
США |
||
|
1 пинта |
= 0,5506 л |
1 пинта |
= 0,473 л |
|
1 кварта |
= 1,136 л |
1 кварта |
= 0,9463 л |
|
1 галлон |
= 4,546 л |
1 галлон |
= 3,785 л |
|
1 пек |
= 9,092 л |
1 пек |
= 8,809 л |
|
1 бушель |
= 36,369 л |
1 бушель |
= 35,24 л |
Вес
|
1 унция |
= 28,35 г |
1 грамм |
|
1 фунт |
= 453,59 г |
1 гектограмм |
|
1 центнер |
= 45,36 г |
1 килограмм |
|
1 короткая тонна |
= 907,18 г |
1 тонна |
Энергия, тепло, работа
|
Единица |
Эквивалентные единицы |
|||
|
кДж |
ккал |
кВт ч |
кГс м |
|
|
кДж |
1 |
0,239 |
0,00278 |
102,0 |
|
ккал |
4,19 |
1 |
0,00116 |
427 |
|
кВт ч |
3600 |
860 |
1 |
367200 |
|
кГс м |
0,00981 |
0,00234 |
2,72 х 106 |
1 |
Давление
|
Пересчет |
В |
||||||
|
Па |
Бар |
мм рт. ст. |
мм вод. ст. |
кгс/см2 |
атм |
||
|
Из |
1 Па |
1 |
10-5 |
7,5 10-3 |
0,102 |
1,02 10-5 |
0,99 10-5 |
|
1 бар |
105 |
1 |
750,1 |
10 200 |
1,02 |
0,987 |
|
|
1 мм рт. ст. |
133 |
13,33 10-4 |
1 |
13,6 |
0,00136 |
0,001316 |
|
|
1 мм вод. ст. |
9,81 |
0,9806 10-4 |
0,07355 |
1 |
0,0001 |
9,68 10-5 |
|
|
1 кгс/см2 |
98 100 |
0,9807 |
735,6 |
10 000 |
1 |
0,968 |
|
|
1 атм |
101 300 |
1,013 |
760 |
10 330 |
1,033 |
1 |
ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ
Общероссийский классификатор единиц измерения (ОКЕИ) ОК 015-94 (МК 002-97)
normativ.kontur.ru
Калькулятор перевода единиц измерения физических величин
calc.ru
❑ ПОМОЩЬ В УЧЕБЕ. ПОПУЛЯРНЫЕ СЕРВИСЫ И УСЛУГИ
TutorOnline
tutoronline.ru
репетиторы м онлайн-курсы для школьников и студентов
Фоксфорд
foxford.ru
онлайн-школа, поможет улучшить оценки, сдать ЕГЭ, ОГЭ
Автор24
a24help.ru
преподаватели и эксперты помогают учиться лучше
Напишем
napishem.ru
помощь в учебе для студентов
Всё сдал
vsesdal.com
онлайн-сервис помощи студентам
Kampus
kampus.ai
получение ответа на любой учебный вопрос в течение 30 минут
Инглекс
englex.ru
занятия по английскому с сильными преподавателями
Ваш Репетитор
repetitors.info
профессиональные репетиторы по всем предметам
Здравствуйте, дорогие друзья! Сегодня мы рассмотрим основные понятия физики и формулы, которые входят в программу учебника Физика 7 класс. Мы пройдем вкратце весь путь познания в области физики от таких базовых понятий, как объем и масса, до коэффициента полезного действия….
Количественные характеристики тела

Объем представляет собой показатель того, сколько место занимает тело в пространстве. Уточним, что, если, к примеру, полая сфера и шар одинакового радиуса находятся в пространстве, то это не означает, что обе фигуры занимают в пространстве одинаковое количество места. Поясним это подробнее.
Полая сфера только на первый взгляд занимает столько же места, сколько шар, на деле их объемы различны – внутри сферы пустота, поэтому, рассчитывая объем, необходимо понимать, что объем воздуха внутри не входит в общую формулу.
Важно! Объем – величина, которая характеризует исключительно место, занимаемое телом. Объем не отражает суть влияние тела на само пространство и на другие тела. Тела одинаковой формы и размеров из совершенно различных материалов будут иметь одинаковые объемы. Формула объема также будет одинакова, как и его численное значение.
Для того чтобы характеризовать понятие объема, вспомним о том, каким образом мы измеряли размеры фигур на плоскости. Для этого мы пользовались понятием площадь. У плоских фигур не может быть объема, у объемных фигур может быть площадь, она называется площадью поверхности. Роль объема в физике очень велика, так как она отражает суть его размеров.
Приведем формулы некоторых фигур:
Формула объема параллелепипеда:
V = abc,
где abc – стороны.
Пирамиды:
,
где S – основание, Н – высота.
Конуса:
,
где R – радиус основания, Н – высота.
Цилиндра:
?=?,
где R – радиус основания, Н – высота.
Говоря о массе, необходимо помнить, что эта физическая величина, в отличие от объема, как раз отражает влияние тела на окружающие тела. Масса представляет собой меру инерции тела, это физическая величина, которая определяет его гравитационные характеристики.
Не следует путать вес с массой, поскольку вес – это сила, и она зависит от гравитационных условий, в котором тело взвешивается.
Путь, время, скорость, ускорение
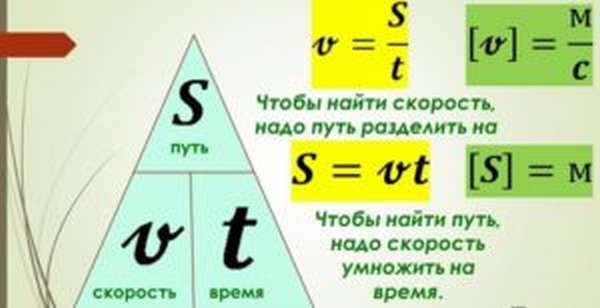
При движении с постоянной скоростью тело проходит за равные промежутки времени равные отрезки пути. Его путь можно отметить формулой:
S = vt, где:
v – скорость тела, t – время его пути. Понятие скорости в физике является одним из самых базовых, поскольку отражает общую тенденцию движущегося тела.
Если в течение времени t1 тело прошло расстояние S1, затем, изменив свою скорость, прошло расстояние S2 за время t2, то есть смысл говорить о таком понятии, как средняя скорость.
Явление средней скорости в общем понимании можно рассматривать как среднее арифметическое двух его скоростей:
.
Если тело обе части пути проходило одно и то же расстояние S, то формула времени принимает вид:
.
Запишем время как отношение расстояния к скорости:
.
Тогда из этого соотношения можно получить выражение для средней скорости:
.
Если тело движется не с постоянной скоростью, но в течение одинаковых промежутков времени, его скорость одинаково меняется, то есть смысл говорить о равноускоренном движении (либо равнозамедленном, если скорость снижается, т.е. тело тормозит).
Важно! Именно равноускоренно двигаются все падающие тела. Ускорение соответствует ускорению свободного падения.
Введем понятие ускорения. Если тело двигалось со скоростью v0, спустя время t оно начало двигаться со скоростью v, то ускорением называется величина, равная:
В математике подобное отношение также называют производной скорости по времени. Зависимость скорости от каждого момента времени легко получить, отделив из формулы ускорения скорость:
.
Изобразим график зависимости скорости от времени:
Очевидно, что графиком является прямая, причем тангенсом угла наклона этой прямой будет ускорение.
Площадь трапеции под графиком – расстояние, которое прошло тело. Вычислить эту площадь довольно просто, нам известно, что площадь трапеции является полусуммой ее оснований, умноженной на высоту. Одно основание трапеции равно v0 (как раз место, где прямая пересекает координату скорости), второе основание равно v. Высотой трапеции является ее сторона – время, т.е. t. Таким образом, площадь трапеции (пройденное расстояние) будет равна:
.
Поскольку v = v0 + at, получаем:
.
Таким образом, при равноускоренном движении расстояние равно:
.
В случае, если речь идет о свободном падении, то вместо ускорения во все формулы должно быть поставлено ускорение свободного падения g=9,81 м/с2.
v = v0 + gt,
Если начальная скорость равна нулю, то:
.
Графиком зависимости пути от времени будет парабола (поскольку зависимость квадратичная):
Постараемся найти формулу времени для разных типов движений:
При равномерном движении:
.
При равноускоренном движении:
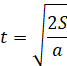
Вес, сила
Если кинематика занимается изучением того, как именно двигаются тела, то динамика подходит к понятию движения более глубоко – она изучают, почему они двигаются именно так. Здесь появляется понятие силы. Что такое сила в динамике? Данная физическая величина численно отражает уровень воздействия одного тела на другое. Измеряется она в ньютонах.
Больше всего физического смысла данной величины отражается в главных четырех законах, которые носят названия Три закона Ньютона и Закон всемирного тяготения.
Первый закон Ньютона гласит, что если сумма всех сил равна нулю, то тело движется равномерно. Не стоит путать сумма всех сил равна нулю и на тело не действуют никакие силы.
Знаменитый второй закон Ньютона устанавливает связь между динамической величиной силы, импульса и ускорения:
,
.
При постоянной массе:
F = ma.
В частности, если ускорение представляет собой ускорение свободного падения g, то сила превращается в вес:
Р = mg
Здесь мы на минуту остановимся и постараемся при помощи этих двух законов Ньютона усвоить несколько важных понятий.
Первый закон Ньютона гласит, что лежащее на поверхности тело хотя и находится в состоянии покоя (относительно земли), тем не менее, на него действуют две силы. Вес:
Р = mg
И нормаль (сила реакции опоры). Сумма этих сил равна нулю. Формула первого закона Ньютона может выглядеть таким образом:
Если .
Вес является величиной относительной с точки зрения планет, на которых находятся тела. Например, часто можно услышать ошибочное высказывание: масса тела на Луне меньше, чем на Земле. Это не так. Массы на всех планетах одинаковые, а вот вес разный, поскольку различается ускорение свободного падения. Именно поэтому космонавты на Луне с такой легкостью подпрыгивали – их вес на Луне был значительно ниже, чем на Земле, ведь Луна их притягивала к себе не так сильно, как Земля.
Третий закон Ньютона гласит, что сила действия равна силе противодействия. Иными словами, чем сильнее мы давим на тело, тем сильнее оно давит на нас. Этот закон отражает равенство силы тяжести и нормали.
.
,
где Fi сила инерции.
Если есть система тел, то скорость центра масс системы равна:
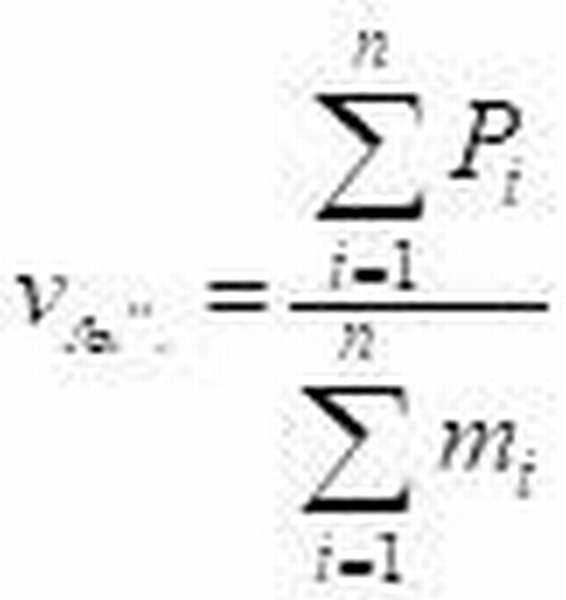
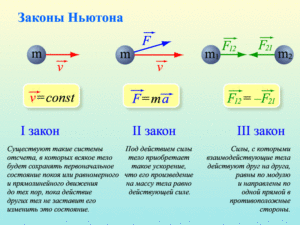
Закон всемирного тяготения, который еще называют четвертым законом Ньютона, гласит:
,
где G – гравитационная постоянная, m1, m2 – массы притягивающихся тел.
Если в левой части этого равенства указать вес, то получаем формулу для ускорения свободного падения тел на любой планете:
.
Также, из закона всемирного тяготения выводится понятие первой космической скорости, т.е. скорости, при которой тело покидает гравитационное поле. Именно до этой скорости (на Земле она равна 7,9 км/с) разгоняют ракеты, которые необходимо вывести на орбиту.
Первая космическая скорость:
.
Вернемся к понятию веса.
Если тело находится в состоянии покоя, то вес равен:
Р = mg
Если тело движется в системе отсчета, которая движется вверх с ускорением а, то вес равен:
Р = m(g+a)
Если тело движется в системе отсчета, которая движется вверх с ускорением а, то вес равен:
Р = m(g-a)
Эта формула наглядно показывает, что в падающем лифте, где а = g, вес тела будет равен нулю, т.е. тело испытает невесомость.
Если тело движется по выпуклой траектории, то ускорение, действующее на него, – центробежное, а значит вес:
Р=m(g-v2/r).
Если тело движется по вогнутой траектории, то ускорение действующее на него тоже центробежное и направлена от центра, а значит вес:
Р=m(g+v2/r).
Формула силы трения:
,
где коэффициент трения, N нормаль (реакция опоры).
Таким образом, мы познакомились уже с несколькими видами сил – вес (сила тяжести), сила трения, центробежная сила, сила всемирного тяготения (которая является по сути тем же весом, только в более общей форме).
Рассмотрим еще одну силу, которая имеет место в случае деформаций. Она называется силой упругости. Закон Гука для малых деформаций (сжатий или растяжений) гласит, что сила, действующая на тело, длину которого деформировали на х, равна:
Fупр = –kx.
Из этого закона вытекает ряд следствий, например модуль Юнга, который выступает коэффициентом пропорциональности в связи между нормальным напряжением и относительным изменением длины:
.

Энергия, работа, мощность, полезное действие
Для того чтобы описывать различные формы взаимодействия материи и ее движение, вводится физическая величина энергия. Если тело прошло расстояние S из-за того, что на него в это время действовала сила F, то энергия этого движения называет работой этого тела. Формула работы записывается таким образом (произведение силы и пройденного пути):
A = FS
Если тело движется со скоростью v, то тело обладает энергией, которая называется кинетической:
.
Если тело приподняли на высоту h, то оно обладает в точке подъеме потенциальной энергией:
E = mgh/.
Важно ! По сути, потенциальная энергия представляет собой работу силы тяжести. Если сила тяжести mg, а путь, пройденный телом, – высота h, на которую его подняли, то работа A = FS = mgh.
При падении тела с высоты Н его потенциальная энергия превращается в кинетическую.
Закон сохранения энергии гласит, что в замкнутых системах энергия сохраняется. Таким образом, если тело подняли на высоту h и отпустили, то скорость, с которой оно будет приземляться, можно вычислить из закона сохранения:
.
Отсюда:
.
Остановимся подробнее на двух законах сохранения: законе сохранения энергии и импульса.
Импульс в замкнутых системах сохраняется, энергия в замкнутых системах сохраняется. В паре эти два закона могут разрешить бесконечное количество задач. Рассмотрим пример.
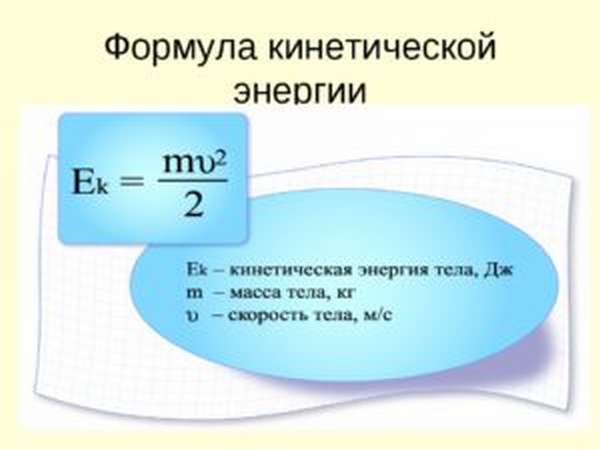
Задача на закон сохранения энергии и импульса
Задача. Идеально упругий шарик массой m движется со скоростью v и ударяется о покоящийся шарик массой M. Удар будет центральный, т.е. траектория шарика и ось между их центрами – одна и та же линия.
Какая будет скорость u шарика массой M и скорость v1 шарика массой m после удара?
Решение:
Первый шарик до столкновения обладал импульсом mv. Второй шарик находился в состоянии покоя, т.е. его импульс был равен M∙0 = 0.
Таким образом, в системе двух шариков суммарный импульс до столкновения был равен:
.
После столкновения импульс первого шарика стал равен mv1, а импульс второго шарика составил Mu. Тогда суммарный импульс системы двух шариков после удара равен:
Согласно закону сохранения импульса Р = Р1, а именно:
(1).
Теперь рассмотрим энергии. Кинетическая энергия первого шарика до удара составила . Кинетическая энергия второго шарика равна нулю. После удара первый шарик имеет кинетическую энергию
. Второй шарик после удара обладает энергией:
.
Согласно закону сохранения энергии:
.
Сократив двойки в знаменателях, получаем:
(2).
Получаем систему из двух выражений (1) и (2).
(*).
Из первого уравнения можем получить выражение для скорости первого шарика после удара:
(3).
Найдем квадрат этой скорости:
.
Найдем значение выражения:
.
Теперь можно подставить это выражение во второе уравнение системы (*):
.
Упрощаем выражение:
.
Выводим квадрат скорости u за скобки:
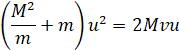
Сокращаем на u:
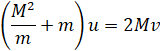
Таким образом, скорость второго шарика после удара составляет:
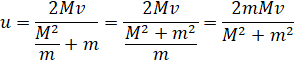
Подставив это в выражение (3), можем найти скорость первого шарика после удара:
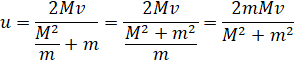
Это был один из немногих примеров того, каким образом при помощи двух законов сохранения находить величины.
Траты энергии. КПД
Однако, говоря об энергии, следует помнить о ее тратах. Например, если во время работы какой-либо физической системы (движущееся тело или тепловая машина) затраченная энергия Q привела к тому, что система произвела полезную энергию A, то говорят о так называемом коэффициенте полезного действия (КПД). КПД измеряется в процентах, которые численно отображают отношение полезной энергии (которую дает система) ко всей суммарно использованной.
Формулу КПД записывают в таком виде:
,
либо, если в процентах:
.
КПД всегда меньше единицы, поскольку полезная работа не может быть больше суммарной, а закон сохранения энергии должен соблюдаться.
Не существует КПД 100%, поскольку траты (даже самые малые) есть в любых системах.
Скорость движения
Сила тяжести вес тела 7 класс
Морфемный разбор слова:
Однокоренные слова к слову:
Список обозначений в физике
Для обозначения физических величин и понятий в физике используются буквы латинского и греческого алфавитов, а также несколько специальных символов и диакритических знаков. Поскольку количество физических величин больше количества букв в латинском и греческом алфавитах, одни и те же буквы используются для обозначения различных величин. Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики.
Связанные понятия
Международная система единиц (СИ) определяет набор из семи основных единиц, из которых формируются все другие единицы измерения. Эти другие единицы называются производными единицами СИ и также считаются частью стандарта.
В математике и информатике подстановка — это операция синтаксической замены подтермов данного терма другими термами, согласно определённым правилам. Обычно речь идёт о подстановке терма вместо переменной.
Надстрочный знак, ве́рхний и́ндекс, суперскри́пт (англ. super script) (типографика) — знак, записанный выше основной строки. Применяется, например, при записи математических и химических формул.
Малые заглавные, или капите́ль (англ. small caps; нем. kapitälchen; от лат. capitellum — головка) — начертание в гарнитуре, в которой строчные знаки выглядят как уменьшенные заглавные. Чтобы подчеркнуть разницу между капителью и строчными буквами, её делают немного выше строчных, а полуапроши капительных знаков увеличивают.
Ѹ, ѹ или Ꙋ, ꙋ (ук или оук, глаголица: Ⱆ) — буква старославянской азбуки. Первоначально диграф букв О и У (точнее, буквы «ик», варианта ижицы) писался горизонтально, но впоследствии, для экономии места, стали использовать вертикальную лигатуру, а впоследствии и вовсе заменили буквой У.
Источник
Что сначала указывается ширина или длина?
Что пишут сначала длину или ширину?
длину буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой. Но если речь идет о геометрической фигуре, например, прямоугольнике, то используется А, высоту или глубину – h, ширину – В.
В каком порядке указываются размеры?
Габаритные размеры изделия длина 1500 мм ширина 1200 мм высота 2500 мм, есть сомнению что может нужно записать 1500×1200×2500, как прописана во многих формулярах изделий, но вот правильности чередования в ГОСТах (длина×ширина×высота или ширина×длина×высота или. )
Как понять где длина и ширина?
Ширина – это протяженность между двумя точками плоскости, которые лежат, в отличие от длины, на наименьшем расстоянии друг от друга. То есть, длина – это наибольший размер предмета, а ширина – наименьшей. Нужно помнить, что ширина всегда измеряется в поперечном направлении к длине.
Как пишется ширина и длина?
длину — буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой. Но если речь идет о геометрической фигуре, например, прямоугольнике, то используется А; высоту или глубину – h; ширину – В.
Где в прямоугольнике длина и ширина?
Как правильно писать размер картины?
Для произведений живописи указываются размеры по подрамнику или по доске (высота, ширина). Для произведений графики указывается двойной размер (высота, ширина) – листа и изображения. это еще в школе учили: оси X и Y. всегда сначала ширина, а потом высота.
Как правильно обозначать размеры?
длину буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой. Но если речь идет о геометрической фигуре, например, прямоугольнике, то используется А, высоту или глубину – h, ширину – В.
Как обозначается высота ширина глубина?
длину — буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой. Но если речь идет о геометрической фигуре, например, прямоугольнике, то используется А, высоту или глубину – h, ширину – В.
Как правильно указать размер шкафа?
Размеры любого шкафа измеряются в трех плоскостях — высота, ширина, глубина, и указываются в миллиметрах, такого размера как длина шкаф не имеет. Стандартные размеры самого простого шкафа — высота 2100, ширина 1300, глубина 600 миллиметров.
Как определить размер посылки?
Как измеряется высота?
Высота в географии, топографии и геодезии может измеряться от разных уровней отсчёта: абсолютная высота отсчитывается от уровня моря или геоида; относительная высота (превышение) отсчитывается от какого-либо условного уровня; геодезическая (эллипсоидальная) высота — высота относительно референц-эллипсоида.
Как в математике обозначается длина и ширина?
Для обозначений могут быть использованы и соответствующие заглавные буквы, в литературе часто встречается сочетание L, B, H (L – длина, В – ширина, Н — высота). Эти же буквы приняты и в физике для обозначения длины, ширины, высоты объектов.
Какой буквой обозначить ширину?
Для обозначений могут быть использованы и соответствующие заглавные буквы, в литературе часто встречается сочетание L, B, H (L – длина, В – ширина, Н — высота). Эти же буквы приняты и в физике для обозначения длины, ширины, высоты объектов.
Какой буквой обозначить длину?
| Длина | |
|---|---|
| Размерность | L |
| Единицы измерения | |
| СИ | м |
| СГС | см |
Как обозначается общая площадь?
В математике и в физике площадь обозначается буквой S заглавной (читается: [эс]). Так, в геометрии этой буквой обозначается площадь любых фигур (треугольника, прямоугольника, квадрата, ромба и т.
Источник
Основная особенность используемых в настоящее время систем единиц состоит в том, что между единицами разных величин имеются определенные соотношения. Эти соотношения установлены теми физическими законами (определениями), которыми связываются между собой измеряемые величины. Так, единица скорости выбрана таким образом, что она выражается через единицы расстояния и времени. При выборе единиц скорости используется определение скорости. Единицу силы, например, устанавливают при помощи второго закона Ньютона.
При построении определенной системы единиц, выбирают несколько физических величин, единицы которых устанавливают независимо друг от друга. Единицы таких величин называют основными. Единицы остальных величин выражают через основные, их называют производными.
Таблица единиц измерения «Пространство и время»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
l, s, d
Протяжённость объекта в одном измерении.
Протяженность объекта в двух измерениях.
Протяжённость объекта в трёх измерениях.
α, φ
Величина изменения направления.
α, β, γ
Быстрота изменения координат тела.
метр в секунду в квадрате
м/с 2
Быстрота изменения скорости объекта.
рад/с =
Скорость изменения угла.
радиан на секунду в квадрате
рад/с 2 =
Быстрота изменения угловой скорости
Таблица единиц измерения «Механика»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Величина, определяющая инерционные и гравитационные свойства тел.
килограмм на кубический метр
кг/м 3
Масса на единицу объёма.
Масса на единицу площади.
кг/м 2
Отношение массы тела к площади его поверхности
Масса на единицу длины.
Отношение массы тела к его линейному параметру
кубический метр на килограмм
м 3 /кг
Объём, занимаемый единицей массы вещества
килограмм в секунду
Масса вещества, которая проходит через заданную площадь поперечного сечения потока за единицу времени
кубический метр в секунду
м 3 /с
Объёмный расход жидкости или газа
килограмм-метр в секунду
кг•м/с
Произведение массы и скорости тела.
экстенсивная, сохраняющаяся величина
килограмм-метр в квадрате в секунду
кг•м 2 /с
Мера вращения объекта.
килограмм-метр в квадрате
кг•м 2
Мера инертности объекта при вращении.
Действующая на объект внешняя причина ускорения.
Произведение силы на длину перпендикуляра, опущенного из точки на линию действия силы.
Произведение силы на время её действия
Давление, механическое напряжение
Па = (кг/(м·с 2 ))
Сила, приходящаяся на единицу площади.
Дж = (кг·м 2 /с 2 )
Скалярное произведение силы и перемещения.
Дж = (кг·м 2 /с 2 )
Способность тела или системы совершать работу.
экстенсивная, сохраняющаяся величина, скаляр
Вт = (кг·м 2 /с 3 )
Скорость изменения энергии.
Таблица единиц измерения «Периодические явления, колебания и волны»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Промежуток времени, за который система совершает одно полное колебание
Частота периодического процесса
Число повторений события за единицу времени.
Циклическая (круговая) частота
рад/с
Циклическая частота электромагнитных колебаний в колебательном контуре.
секунда в минус первой степени
Периодический процесс, равный числу полных циклов, совершённых за единицу времени.
Расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
метр в минус первой степени
Пространственная частота волны
Таблица единиц измерения «Тепловые явления»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Средняя кинетическая энергия частиц объекта.
кельвин в минус первой степени
Зависимость электрического сопротивления от температуры
gradT
Изменение температуры на единицу длины в направлении распространения теплоты.
Теплота (количество теплоты)
Дж = (кг·м 2 /с 2 )
Энергия, передаваемая от одного тела к другому немеханическим путём
джоуль на килограмм
Дж/кг
Кол-во теплоты, которое необходимо подвести к веществу, взятому при температуре плавления, чтобы расплавить его.
Кол-во теплоты, поглощаемой (выделяемой) телом в процессе нагревания.
джоуль на килограмм-кельвин
Дж/(кг•К)
Теплоёмкость единичной массы вещества.
джоуль на килограмм
Дж/кг
Мера необратимого рассеивания энергии или бесполезности энергии.
Таблица единиц измерения «Молекулярная физика»
Физическая величина
Символ
Единица измерения физической величины
Описание
Примечания
моль
Количество однотипных структурных единиц, из которых состоит вещество.
M, μ
кг/моль
Отношение массы вещества к количеству молей этого вещества.
Дж/моль
Энергия термодинамической системы.
джоуль на моль-кельвин
Дж/(моль•К)
Теплоёмкость одного моля вещества.
метр в минус третьей степени
Число молекул, содержащихся в единице объема.
килограмм на кубический метр
кг/м 3
Отношение массы компонента, содержащегося в смеси, к объёму смеси.
моль на кубический метр
моль/м 3
Содержание компонента относительно всей смеси.
В, μ
квадратный метр на вольт-секунду
м 2 /(В•с)
Коэффициент пропорциональности между дрейфовой скоростью носителей и приложенным внешним электрическим полем.
Таблица единиц измерения «Электричество и магнетизм»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Протекающий в единицу времени заряд.
ампер на квадратный метр
А/м 2
Сила электрического тока, протекающего через элемент поверхности единичной площади.
Кл = (А·с)
Способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии.
экстенсивная, сохраняющаяся величина
Электрический дипольный момент
Электрические свойства системы заряженных частиц в смысле создаваемого ею поля и действия на неё внешних полей.
кулон на квадратный метр
Кл/м 2
Процессы и состояния, связанные с разделением каких-либо объектов, преимущественно в пространстве.
Изменение потенциальной энергии, приходящееся на единицу заряда.
Работа сторонних сил (некулоновских) по перемещению заряда.
Отношение силы F, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда q
Мера способности проводника накапливать электрический заряд
Ом = (м 2 ·кг/(с 3 ·А 2 ))
сопротивление объекта прохождению электрического тока
Удельное электрическое сопротивление
Способность материала препятствовать прохождению электрического тока
Способность тела (среды) проводить электрический ток
Векторная величина, являющаяся силовой характеристикой магнитного поля
Величина, учитывающая интенсивность магнитного поля и занимаемую им область.
Напряженность магнитного поля
Разность вектора магнитной индукции B и вектора намагниченности M
А•м 2
Величина, характеризующая магнитные свойства вещества
Величина, характеризующая магнитное состояние макроскопического физического тела.
Коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и полным магнитным потоком
Дж = (кг·м 2 /с 2 )
Энергия, заключенная в электромагнитном поле
Объемная плотность энергии
джоуль на кубический метр
Дж/м 3
Энергия электрического поля конденсатора
Мощность в цепи переменного тока
Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока
Суммарная мощность с учетом активной и реактивной ее составляющих, а также отклонения формы тока и напряжения от гармонической
Таблица единиц измерения «Оптика, электромагнитное излучение»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Количество световой энергии, излучаемой в заданном направлении в единицу времени.
Световая, экстенсивная величина
Физическая величина, характеризующая количество «световой» мощности в соответствующем потоке излучения
Физическая величина, характеризует способность энергии, переносимой светом, вызывать у человека зрительные ощущения
Отношение светового потока, падающего на малый участок поверхности, к его площади.
люмен на квадратный метр
лм/м 2
Световая величина, представляющая собой световой поток
кандела на квадратный метр
кд/м 2
Сила света, излучаемая единицей площади поверхности в определенном направлении
Дж = (кг·м 2 /с 2 )
Энергия, переносимая оптическим излучением
Таблица единиц измерения «Акустика»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Переменное избыточное давление, возникающее в упругой среде при прохождении через неё звуковой волны
кубический метр в секунду
м 3 /с
Отношение объема сырья, подаваемого в реактор в час к объему катализатора
Скорость распространения упругих волн в среде
ватт на квадратный метр
Вт/м 2
Величина, характеризующая мощность, переносимую звуковой волной в направлении распространения
скалярная физическая величина
паскаль-секунда на кубический метр
Па•с/м 3
Отношение амплитуды звукового давления в среде к колебательной скорости её частиц при прохождении через среду звуковой волны
ньютон-секунда на метр
Указывает силу, необходимую для движения тела при каждой частоте
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Масса объекта, находящегося в состоянии покоя.
Величина, выражающая влияние внутренних взаимодействий на массу составной частицы
Элементарный электрический заряд
Минимальная порция (квант) электрического заряда, наблюдающегося в природе у свободных долгоживущих частиц
Дж = (кг·м 2 /с 2 )
Разность между энергией состояния, в котором составляющие части системы бесконечно удалены
Период полураспада, среднее время жизни
Время, в течение которого система распадается в примерном отношении 1/2
Величина, характеризующая вероятность взаимодействия элементарной частицы с атомным ядром или другой частицей
Величина, равная отношению общего числа распадов радиоактивных ядер нуклида в источнике ко времени распада
Энергия ионизирующего излучения
Дж = (кг·м 2 /с 2 )
Вид энергии, высвобождаемой атомами в форме электромагнитных волн (гамма- или рентгеновское излучение) или частиц
Поглощенная доза ионизирующего излучения
Доза, при которой массе 1 кг передаётся энергия ионизирующего излучения в 1 джоул
Эквивалентная доза ионизирующего излучения
Поглощенная доза любого ионизирующего излучения, равная 100 эрг на 1 грамм облученного вещества
Экспозиционная доза рентгеновского и гамма-излучения
кулон на килограмм
Кл/кг
отношение суммарного электрического заряда ионов одного знака от внешнего гамма-излучения
Обозначения в физике с несколькими буквами
Специальные символы
Для удобства написания и чтения в среде ученых физиков принято использовать специальные символы, характеризующие те или иные явления и свойства.
Скобки
В физике принято использовать не только формулы, которые применяют в математике, но и специализированные скобки.
Диакритические знаки
Диакритические знаки добавляются к символу физической величины для обозначения определённых различий. Ниже диакритические знаки добавлены для примера к букве x.
Источник
Обозначения : Основные физические величины
Механические величины
Коэффициент жесткости (жесткость)
Коэффициент запаса прочности
Коэффициент полезного действия
Коэффициент трения качения
Коэффициент трения скольжения
Ускорение свободного падения
Акустические величины
Тепловые величины и величины молекулярной физики
Температура по шкале Цельсия
Газовая постоянная (молярная)
Температурный коэффициент линейного расширения
Коэффициент полезного действия
Температурный коэффициент объемного расширения
Относительная молекулярная масса
Удельная теплота парообразования
Постоянная (число) Авогадро
Удельная теплота плавления
Удельная теплота сгорания топлива (сокр: теплота сгорания топлива)
Постоянная (число) Лошмидта
Электрические и магнитные величины
Температурный коэффициент электрического сопротивления
Диэлектрическая проницаемость вакуума (электрическая постоянная)
Удельная плотность энергии магнитного поля
Удельная плотность энергии электрического поля
Удельная электрическая проводимость
Удельное электрическое сопротивление
Частота электрического тока
Магнитная проницаемость вакуума (магнитная постоянная)
Число витков обмотки
Мощность электрической цепи
Напряженность магнитного поля
Напряженность электрического поля
Электрический момент диполя молекулы
Объемная плотность электрического заряда
Электрический заряд (количество электричества)
Относительная диэлектрическая проницаемость
Относительная магнитная проницаемость
Поверхностная плотность заряда
Плотность электрического тока
Постоянная (число) Фарадея
Работа выхода электрона
Энергия магнитного поля
Энергия электрического поля
Оптические величины
Увеличение окуляра, микроскопа, лупы
Угол отражения луча
Плотность потока излучения
Показатель (коэффициент) преломления
Величины атомной физики
Относительная атомная масса
Величины ионизирующих излучений
Поглощенная доза излучения (доза излучения)
Мощность поглощенной дозы излучения
Активность нуклида в радиоактивном источнике
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
О сайте
На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.
Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.
calcsbox.com
На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.
© 2021 Все калькуляторы online
Копирование материалов запрещено
Источник
Что сначала указывается ширина или длина?
Что пишут сначала длину или ширину?
длину буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой. Но если речь идет о геометрической фигуре, например, прямоугольнике, то используется А, высоту или глубину – h, ширину – В.
В каком порядке указываются размеры?
Габаритные размеры изделия длина 1500 мм ширина 1200 мм высота 2500 мм, есть сомнению что может нужно записать 1500×1200×2500, как прописана во многих формулярах изделий, но вот правильности чередования в ГОСТах (длина×ширина×высота или ширина×длина×высота или. )
Как понять где длина и ширина?
Ширина – это протяженность между двумя точками плоскости, которые лежат, в отличие от длины, на наименьшем расстоянии друг от друга. То есть, длина – это наибольший размер предмета, а ширина – наименьшей. Нужно помнить, что ширина всегда измеряется в поперечном направлении к длине.
Как пишется ширина и длина?
длину — буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой. Но если речь идет о геометрической фигуре, например, прямоугольнике, то используется А; высоту или глубину – h; ширину – В.
Где в прямоугольнике длина и ширина?
Как правильно писать размер картины?
Для произведений живописи указываются размеры по подрамнику или по доске (высота, ширина). Для произведений графики указывается двойной размер (высота, ширина) – листа и изображения. это еще в школе учили: оси X и Y. всегда сначала ширина, а потом высота.
Как правильно обозначать размеры?
длину буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой. Но если речь идет о геометрической фигуре, например, прямоугольнике, то используется А, высоту или глубину – h, ширину – В.
Как обозначается высота ширина глубина?
длину — буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой. Но если речь идет о геометрической фигуре, например, прямоугольнике, то используется А, высоту или глубину – h, ширину – В.
Как правильно указать размер шкафа?
Размеры любого шкафа измеряются в трех плоскостях — высота, ширина, глубина, и указываются в миллиметрах, такого размера как длина шкаф не имеет. Стандартные размеры самого простого шкафа — высота 2100, ширина 1300, глубина 600 миллиметров.
Как определить размер посылки?
Как измеряется высота?
Высота в географии, топографии и геодезии может измеряться от разных уровней отсчёта: абсолютная высота отсчитывается от уровня моря или геоида; относительная высота (превышение) отсчитывается от какого-либо условного уровня; геодезическая (эллипсоидальная) высота — высота относительно референц-эллипсоида.
Как в математике обозначается длина и ширина?
Для обозначений могут быть использованы и соответствующие заглавные буквы, в литературе часто встречается сочетание L, B, H (L – длина, В – ширина, Н — высота). Эти же буквы приняты и в физике для обозначения длины, ширины, высоты объектов.
Какой буквой обозначить ширину?
Для обозначений могут быть использованы и соответствующие заглавные буквы, в литературе часто встречается сочетание L, B, H (L – длина, В – ширина, Н — высота). Эти же буквы приняты и в физике для обозначения длины, ширины, высоты объектов.
Какой буквой обозначить длину?
| Длина | |
|---|---|
| Размерность | L |
| Единицы измерения | |
| СИ | м |
| СГС | см |
Как обозначается общая площадь?
В математике и в физике площадь обозначается буквой S заглавной (читается: [эс]). Так, в геометрии этой буквой обозначается площадь любых фигур (треугольника, прямоугольника, квадрата, ромба и т.
Источник
Теперь вы знаете какие однокоренные слова подходят к слову Как пишется размер в физике, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову «Как пишется размер в физике», предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором.
Измерение величин
- Меры
- Единицы измерения
- Сокращённые наименования мер
- Измерительные приборы
Величина — это то, что можно измерить. Такие понятия, как длина, площадь, объём, масса, время, скорость и т. д. называют величинами. Величина является результатом измерения, она определяется числом, выраженным в определённых единицах. Единицы, в которых измеряется величина, называют единицами измерения.
Для обозначения величины пишут число, а рядом название единицы, в которой она измерялась. Например, 5 см, 10 кг, 12 км, 5 мин. Каждая величина имеет бесчисленное множество значений, например длина может быть равна: 1 см, 2 см, 3 см и т. д.
Одна и та же величина может быть выражена в разных единицах, например килограмм, грамм и тонна — это единицы измерения веса. Одна и та же величина в разных единицах выражается разными числами. Например:
5 см = 50 мм (длина),
1 ч = 60 мин (время),
2 кг = 2000 г (вес).
Измерить величину — значит узнать, сколько раз в ней содержится другая величина того же рода, принятая за единицу измерения.
Например, мы хотим узнать точную длину какой-нибудь комнаты. Значит нам нужно измерить эту длину при помощи другой длины, которая нам хорошо известна, например при помощи метра. Для этого откладываем метр по длине комнаты столько раз, сколько можно. Если он уложится по длине комнаты ровно 7 раз, то длина её равна 7 метрам.
В результате измерения величины получается или именованное число, например 12 метров, или несколько именованных чисел, например 5 метров 7 сантиметров, совокупность которых называется составным именованным числом.
Меры
В каждом государстве правительство установило определённые единицы измерения для различных величин. Точно рассчитанная единица измерения, принятая в качестве образца, называется эталоном или образцовой единицей. Сделаны образцовые единицы метра, килограмма, сантиметра и т. п., по которым изготавливают единицы для обиходного употребления. Единицы, вошедшие в употребление и утверждённые государством, называются мерами.
Меры называются однородными, если они служат для измерения величин одного рода. Так, грамм и килограмм — меры однородные, так как они служат для измерения веса.
Единицы измерения
Ниже представлены единицы измерения различных величин, которые часто встречаются в задачах по математике:
Меры веса/массы:
- 1 тонна = 10 центнеров;
- 1 центнер = 100 килограмм;
- 1 килограмм = 1000 грамм;
- 1 грамм = 1000 миллиграмм.
Меры длины:
- 1 километр = 1000 метров;
- 1 метр = 10 дециметров;
- 1 дециметр = 10 сантиметров;
- 1 сантиметр = 10 миллиметров.
Меры площади (квадратные меры):
- 1 кв. километр = 100 гектарам;
- 1 гектар = 10000 кв. метрам;
- 1 кв. метр = 10000 кв. сантиметров;
- 1 кв. сантиметр = 100 кв. миллиметрам.
Меры объёма (кубические меры):
- 1 куб. метр = 1000 куб. дециметров;
- 1 куб. дециметр = 1000 куб. сантиметров;
- 1 куб. сантиметр = 1000 куб. миллиметров.
Рассмотрим ещё такую величину как литр. Для измерения вместимости сосудов употребляется литр. Литр является объёмом, который равен одному кубическому дециметру (1 литр = 1 куб. дециметру).
Меры времени:
- 1 век (столетие) = 100 годам;
- 1 год = 12 месяцам;
- 1 месяц = 30 суткам;
- 1 неделя = 7 суткам;
- 1 сутки = 24 часам;
- 1 час = 60 минутам;
- 1 минута = 60 секундам;
- 1 секунда = 1000 миллисекундам.
Кроме того, используют такие единицы измерения времени, как квартал и декада.
- квартал — 3 месяца;
- декада — 10 суток.
Месяц принимается за 30 дней, если не требуется определить число и название месяца. Январь, март, май, июль, август, октябрь и декабрь — 31 день. Февраль в простом году — 28 дней, февраль в високосном году — 29 дней. Апрель, июнь, сентябрь, ноябрь — 30 дней.
Год представляет собой (приблизительно) то время, в течении которого Земля совершает полный оборот вокруг Солнца. Принято считать каждые три последовательных года по 365 дней, а следующий за ними четвёртый — в 366 дней. Год, содержащий в себе 366 дней, называется високосным, а годы, содержащие по 365 дней — простыми. К четвёртому году добавляют один лишний день по следующей причине. Время обращения Земли вокруг Солнца содержит в себе не ровно 365 суток, а 365 суток и 6 часов (приблизительно). Таким образом, простой год короче истинного года на 6 часов, а 4 простых года короче 4 истинных годов на 24 часа, т. е. на одни сутки. Поэтому к каждому четвёртому году добавляют одни сутки (29 февраля).
Об остальных видах величин вы узнаете по мере дальнейшего изучения различных наук.
Сокращённые наименования мер
Сокращённые наименования мер принято записывать без точки:
Меры длины
|
Меры веса/массы
|
Меры площади (квадратные меры)
|
Меры объёма (кубические меры)
|
Меры времени
|
Мера вместимости сосудов
|
 |
1 мм | 1 см | 1 дм | 1 м | 1 км |
 |
1 мм2 | 1 см2 | 1 дм2 | 1 м2 | 1 км2 |
 |
1 мм3 | 1 см3 | 1 дм3 | 1 м3 | 1 км3 |
Измерительные приборы
Для измерения различных величин используются специальные измерительные приборы. Одни из них очень просты и предназначены для простых измерений. К таким приборам можно отнести измерительную линейку, рулетку, измерительный цилиндр и др. Другие измерительные приборы более сложные. К таким приборам можно отнести секундомеры, термометры, электронные весы и др.
Измерительные приборы, как правило, имеют измерительную шкалу (или кратко шкалу). Это значит, что на приборе нанесены штриховые деления, и рядом с каждым штриховым делением написано соответствующее значение величины. Расстояние между двумя штрихами, возле которых написано значение величины, может быть дополнительно разделено ещё на несколько более малых делений, эти деления чаще всего не обозначены числами.
Определить, какому значению величины соответствует каждое самое малое деление, не трудно. Так, например, на рисунке ниже изображена измерительная линейка:
Цифрами 1, 2, 3, 4 и т. д. обозначены расстояния между штрихами, которые разделены на 10 одинаковых делений. Следовательно, каждое деление (расстояние между ближайшими штрихами) соответствует 1 мм. Эта величина называется ценой деления шкалы измерительного прибора.
Перед тем как приступить к измерению величины, следует определить цену деления шкалы используемого прибора.
Для того чтобы определить цену деления, необходимо:
- Найти два ближайших штриха шкалы, возле которых написаны значения величины.
- Вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.
В качестве примера определим цену деления шкалы термометра, изображённого на рисунке слева.
Возьмём два штриха, около которых нанесены числовые значения измеряемой величины (температуры).
Например, штрихи с обозначениями 20 °С и 30 °С. Расстояние между этими штрихами разделено на 10 делений. Таким образом, цена каждого деления будет равна:
(30 °С — 20 °С) : 10 = 1 °С
Следовательно, термометр показывает 47 °С.
Измерять различные величины в повседневной жизни приходится постоянно каждому из нас. Например, чтобы прийти вовремя в школу или на работу, приходится измерять время, которое будет потрачено на дорогу. Метеорологи для предсказания погоды измеряют температуру, атмосферное давление, скорость ветра и т. д.