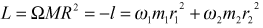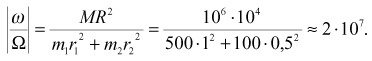Illuminated illustration depicting the wolf, goat and cabbage problem in the Ormesby Psalter, dating to 1250–1330
The wolf, goat and cabbage problem is a river crossing puzzle. It dates back to at least the 9th century,[1] and has entered the folklore of several cultures.[2][3]
The story[edit]
A farmer went to a market and purchased a wolf, a goat, and a cabbage. On his way home, the farmer came to the bank of a river and rented a boat. But crossing the river by boat, the farmer could carry only himself and a single one of his purchases: the wolf, the goat, or the cabbage.
If left unattended together, the wolf would eat the goat, or the goat would eat the cabbage.
The farmer’s challenge was to carry himself and his purchases to the far bank of the river, leaving each purchase intact.
Solution[edit]
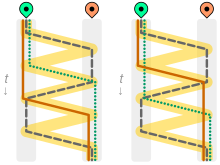
The two solutions with the vertical axis denoting time, and brown, grey, green and beige paths denoting the wolf, goat, cabbage and boat, respectively
The first step that must be taken is to let the goat go across the river, as any other actions will result in the goat or the cabbage being eaten. When the farmer returns to the original side, he has the choice of taking either the wolf or the cabbage across next. If he takes the wolf across, he would have to return to get the cabbage, resulting in the wolf eating the goat. If he takes the cabbage across second, he will need to return to get the wolf, resulting in the cabbage being eaten by the goat. The dilemma is solved by taking the wolf (or the cabbage) over and bringing the goat back. Now he can take the cabbage (or the wolf) over, and finally return to fetch the goat.
An animation of the solution
His actions in the solution are summarized in the following steps:
- Take the goat over
- Return to other side
- Take the wolf or cabbage over
- Return with the goat
- Take the cabbage or wolf over
- Return
- Take goat over
Thus there are seven crossings, four forward and three back.
Note: the key to the solution is realizing that one can bring things back (emphasized above). This is often unclear from the wording of the story, but never forbidden. Knowing this will make the problem easy to solve even by small children. The focus of the puzzle is not just task scheduling, but creative thinking, similarly to the Nine dots puzzle.
Visualisation of the moves possible in the puzzle. Uppercase letters denote the Fox, Goose and Beans at the destination, and lowercase ones denote them at the origin. Movement of each object is represented by a coordinate axis. All the 8 valid and invalid placements are shown as vertices of a cube, and all 12 movements as its edges. Invalid moves are crossed out, leaving the 2 solutions shown in blue and purple.
Occurrence and variations[edit]
The puzzle is one of a number of river crossing puzzles, where the object is to move a set of items across a river subject to various restrictions.
In the earliest known occurrence of this problem, in the medieval manuscript Propositiones ad Acuendos Juvenes, the three objects are a wolf, a goat, and a cabbage, but other cosmetic variations of the puzzle also exist, such as: wolf, sheep, and cabbage;[4][2], p. 26 fox, chicken, and grain;[5] fox, goose and corn;[6] and panther, pig, and porridge.[7] The logic of the puzzle, in which there are three objects, A, B, and C, such that neither A and B nor B and C can be left together, remains the same.
Another version of the puzzle stemming from a Chinese legend is recorded in an 18th-century painted panel by Japanese artist Maruyama Ōkyo, in the collection of the British museum. According to the legend, when a tiger has three cubs, one of them will be a leopard rather than a tiger, and more fierce than the others. Following this legend, the subject of a tiger with her cubs became a traditional subject for art in east Asia.[8] The depiction by Ōkyo shows the tiger family crossing a river, with the mother carrying one cub across the river at a time. This depicts a puzzle equivalent to the puzzle of the wolf, goat, and cabbage, asking how the mother can do this without leaving the leopard cub alone with any of the other tiger cubs.[9] The same variation of the puzzle has also been recorded as a koan of Ryōan-ji, a Zen temple in Kyoto.[10]
The puzzle has been found in the folklore of African-Americans, Cameroon, the Cape Verde Islands, Denmark, Ethiopia, Ghana, Italy, Romania, Russia, Scotland, the Sudan, Uganda, Zambia, and Zimbabwe.[2], pp. 26–27;[11] It has been given the index number H506.3 in Stith Thompson’s motif index of folk literature, and is ATU 1579 in the Aarne–Thompson classification system.[12]
The puzzle was a favorite of Lewis Carroll,[13] and has been reprinted in various collections of recreational mathematics.[2], p. 26.
In his ‘Arabian Nights’ memoir, Meetings with Remarkable Men, the metaphysical Magus, G. I. Gurdjieff cites this riddle as «The Wolf, the goat and the cabbage». He notes, «This popular riddle clearly shows that…not solely by means of the ingenuity which every normal man should have, but that in addition he must not be lazy nor spare his strength, but must cross the river extra times for the attainment of his aim.»
Variations of the puzzle also appear in the adventure game Broken Sword: The Sleeping Dragon, the Nintendo DS puzzle game Professor Layton and the Curious Village, and in The Simpsons episode «Gone Maggie Gone», where Homer has to get across a river with Maggie, Santa’s Little Helper, and a jar of rat poison that looks like candy. In the Class of 3000 episode «Westley Side Story», Sunny and his students perform a similar exercise involving a chicken, a coyote and a sack of corn. The Between the Lions episode «Farmer Ken’s Puzzle» portrays it being made into a computer game with a cat, a hen, and a sack of seeds.
Interactive chicken, fox and grain problem.
In the Bull episode «Justice for Cable», Benny begins a riddle with «a man has a fox, a duck, and a bag of beans». Bull inexplicably declares «There is no answer», and everyone believes him.[14]
In some parts of Africa, variations on the puzzle have been found in which the boat can carry two objects instead of only one. When the puzzle is weakened in this way it is possible to introduce the extra constraint that no two items, including A and C, can be left together.[2], p. 27.
In the Star Trek: Prodigy episode «Time Amok», a holographic version of Kathryn Janeway employs the tale (here told as the chicken, fox and grain problem) to teach the crew of the USS Protostar how to work together.
See also[edit]
- Missionaries and cannibals problem
References[edit]
- ^ Pressman, Ian; David Singmaster (June 1989). ««The Jealous Husbands» and «The Missionaries and Cannibals»«. The Mathematical Gazette. The Mathematical Association. 73 (464): 73–81. doi:10.2307/3619658. JSTOR 3619658.
- ^ a b c d e Ascher, Marcia (February 1990). «A River-Crossing Problem in Cross-Cultural Perspective». Mathematics Magazine. Mathematical Association of America. 63 (1): 26–29. doi:10.2307/2691506. JSTOR 2691506.
- ^ Gurdjieff, G. I. (1963). Meetings with Remarkable Men (1st English ed.). London: Routledge & Kegan Paul. pp. 4–5.
- ^ Alcuin’s Transportation Problems and Integer Programming Archived 2011-07-19 at the Wayback Machine,
Ralf Borndörfer, Martin Grötschel, and Andreas Löbel, preprint SC-95-27 (November 1995), Konrad-Zuse-Zentrum für Informationstechnik Berlin. - ^ The Classic River Crossing Puzzle Archived 2008-06-17 at the Wayback Machine
- ^ Mary Jane Sterling, Math Word Problems for Dummies, p. 313
- ^ Stewart, Ian (1998). The Magical Maze. Phoenix. ISBN 0-7538-0514-6.
- ^ Sung, Hou-Mei (2004). «Tiger with cubs: A rediscovered Ming court painting». Artibus Asiae. 64 (2): 281–293. JSTOR 3250187.
- ^ «A tiger’s tale: British Museum buys rare Japanese screen». Art Fund. 20 October 2006. Retrieved 2021-01-08.
- ^ Goto, Seiko; Naka, Takahiro (2015). Japanese Gardens: Symbolism and Design. Routledge. p. 20. ISBN 9781317411642.
- ^ Evans-Pritchard, E. E. (1962). «235. Three Zande Texts». Man. 62: 149–152. doi:10.2307/2796709. JSTOR 2796709.
- ^ «Carrying a Wolf, a Goat, and a Cabbage across the Stream. Metamorphoses of ATU 1579», Piret Voolaid, Folklore: Electronic Journal of Folklore 35 (2007), pp. 111–130. Tartu: Eesti Kirjandusmuuseum.
- ^ p. 17, Rediscovered Lewis Carroll Puzzles, Lewis Carroll, compiled by Edward Wakeling, Courier Dover Publications, 1996, ISBN 0-486-28861-7.
- ^ «Springfield! Springfield!».
External links[edit]
- Goat, Cabbage and Wolf A Javascript simulation
- Fox, Chook and Corn A simulation without Javascript needed
Illuminated illustration depicting the wolf, goat and cabbage problem in the Ormesby Psalter, dating to 1250–1330
The wolf, goat and cabbage problem is a river crossing puzzle. It dates back to at least the 9th century,[1] and has entered the folklore of several cultures.[2][3]
The story[edit]
A farmer went to a market and purchased a wolf, a goat, and a cabbage. On his way home, the farmer came to the bank of a river and rented a boat. But crossing the river by boat, the farmer could carry only himself and a single one of his purchases: the wolf, the goat, or the cabbage.
If left unattended together, the wolf would eat the goat, or the goat would eat the cabbage.
The farmer’s challenge was to carry himself and his purchases to the far bank of the river, leaving each purchase intact.
Solution[edit]
The two solutions with the vertical axis denoting time, and brown, grey, green and beige paths denoting the wolf, goat, cabbage and boat, respectively
The first step that must be taken is to let the goat go across the river, as any other actions will result in the goat or the cabbage being eaten. When the farmer returns to the original side, he has the choice of taking either the wolf or the cabbage across next. If he takes the wolf across, he would have to return to get the cabbage, resulting in the wolf eating the goat. If he takes the cabbage across second, he will need to return to get the wolf, resulting in the cabbage being eaten by the goat. The dilemma is solved by taking the wolf (or the cabbage) over and bringing the goat back. Now he can take the cabbage (or the wolf) over, and finally return to fetch the goat.
An animation of the solution
His actions in the solution are summarized in the following steps:
- Take the goat over
- Return to other side
- Take the wolf or cabbage over
- Return with the goat
- Take the cabbage or wolf over
- Return
- Take goat over
Thus there are seven crossings, four forward and three back.
Note: the key to the solution is realizing that one can bring things back (emphasized above). This is often unclear from the wording of the story, but never forbidden. Knowing this will make the problem easy to solve even by small children. The focus of the puzzle is not just task scheduling, but creative thinking, similarly to the Nine dots puzzle.
Visualisation of the moves possible in the puzzle. Uppercase letters denote the Fox, Goose and Beans at the destination, and lowercase ones denote them at the origin. Movement of each object is represented by a coordinate axis. All the 8 valid and invalid placements are shown as vertices of a cube, and all 12 movements as its edges. Invalid moves are crossed out, leaving the 2 solutions shown in blue and purple.
Occurrence and variations[edit]
The puzzle is one of a number of river crossing puzzles, where the object is to move a set of items across a river subject to various restrictions.
In the earliest known occurrence of this problem, in the medieval manuscript Propositiones ad Acuendos Juvenes, the three objects are a wolf, a goat, and a cabbage, but other cosmetic variations of the puzzle also exist, such as: wolf, sheep, and cabbage;[4][2], p. 26 fox, chicken, and grain;[5] fox, goose and corn;[6] and panther, pig, and porridge.[7] The logic of the puzzle, in which there are three objects, A, B, and C, such that neither A and B nor B and C can be left together, remains the same.
Another version of the puzzle stemming from a Chinese legend is recorded in an 18th-century painted panel by Japanese artist Maruyama Ōkyo, in the collection of the British museum. According to the legend, when a tiger has three cubs, one of them will be a leopard rather than a tiger, and more fierce than the others. Following this legend, the subject of a tiger with her cubs became a traditional subject for art in east Asia.[8] The depiction by Ōkyo shows the tiger family crossing a river, with the mother carrying one cub across the river at a time. This depicts a puzzle equivalent to the puzzle of the wolf, goat, and cabbage, asking how the mother can do this without leaving the leopard cub alone with any of the other tiger cubs.[9] The same variation of the puzzle has also been recorded as a koan of Ryōan-ji, a Zen temple in Kyoto.[10]
The puzzle has been found in the folklore of African-Americans, Cameroon, the Cape Verde Islands, Denmark, Ethiopia, Ghana, Italy, Romania, Russia, Scotland, the Sudan, Uganda, Zambia, and Zimbabwe.[2], pp. 26–27;[11] It has been given the index number H506.3 in Stith Thompson’s motif index of folk literature, and is ATU 1579 in the Aarne–Thompson classification system.[12]
The puzzle was a favorite of Lewis Carroll,[13] and has been reprinted in various collections of recreational mathematics.[2], p. 26.
In his ‘Arabian Nights’ memoir, Meetings with Remarkable Men, the metaphysical Magus, G. I. Gurdjieff cites this riddle as «The Wolf, the goat and the cabbage». He notes, «This popular riddle clearly shows that…not solely by means of the ingenuity which every normal man should have, but that in addition he must not be lazy nor spare his strength, but must cross the river extra times for the attainment of his aim.»
Variations of the puzzle also appear in the adventure game Broken Sword: The Sleeping Dragon, the Nintendo DS puzzle game Professor Layton and the Curious Village, and in The Simpsons episode «Gone Maggie Gone», where Homer has to get across a river with Maggie, Santa’s Little Helper, and a jar of rat poison that looks like candy. In the Class of 3000 episode «Westley Side Story», Sunny and his students perform a similar exercise involving a chicken, a coyote and a sack of corn. The Between the Lions episode «Farmer Ken’s Puzzle» portrays it being made into a computer game with a cat, a hen, and a sack of seeds.
Interactive chicken, fox and grain problem.
In the Bull episode «Justice for Cable», Benny begins a riddle with «a man has a fox, a duck, and a bag of beans». Bull inexplicably declares «There is no answer», and everyone believes him.[14]
In some parts of Africa, variations on the puzzle have been found in which the boat can carry two objects instead of only one. When the puzzle is weakened in this way it is possible to introduce the extra constraint that no two items, including A and C, can be left together.[2], p. 27.
In the Star Trek: Prodigy episode «Time Amok», a holographic version of Kathryn Janeway employs the tale (here told as the chicken, fox and grain problem) to teach the crew of the USS Protostar how to work together.
See also[edit]
- Missionaries and cannibals problem
References[edit]
- ^ Pressman, Ian; David Singmaster (June 1989). ««The Jealous Husbands» and «The Missionaries and Cannibals»«. The Mathematical Gazette. The Mathematical Association. 73 (464): 73–81. doi:10.2307/3619658. JSTOR 3619658.
- ^ a b c d e Ascher, Marcia (February 1990). «A River-Crossing Problem in Cross-Cultural Perspective». Mathematics Magazine. Mathematical Association of America. 63 (1): 26–29. doi:10.2307/2691506. JSTOR 2691506.
- ^ Gurdjieff, G. I. (1963). Meetings with Remarkable Men (1st English ed.). London: Routledge & Kegan Paul. pp. 4–5.
- ^ Alcuin’s Transportation Problems and Integer Programming Archived 2011-07-19 at the Wayback Machine,
Ralf Borndörfer, Martin Grötschel, and Andreas Löbel, preprint SC-95-27 (November 1995), Konrad-Zuse-Zentrum für Informationstechnik Berlin. - ^ The Classic River Crossing Puzzle Archived 2008-06-17 at the Wayback Machine
- ^ Mary Jane Sterling, Math Word Problems for Dummies, p. 313
- ^ Stewart, Ian (1998). The Magical Maze. Phoenix. ISBN 0-7538-0514-6.
- ^ Sung, Hou-Mei (2004). «Tiger with cubs: A rediscovered Ming court painting». Artibus Asiae. 64 (2): 281–293. JSTOR 3250187.
- ^ «A tiger’s tale: British Museum buys rare Japanese screen». Art Fund. 20 October 2006. Retrieved 2021-01-08.
- ^ Goto, Seiko; Naka, Takahiro (2015). Japanese Gardens: Symbolism and Design. Routledge. p. 20. ISBN 9781317411642.
- ^ Evans-Pritchard, E. E. (1962). «235. Three Zande Texts». Man. 62: 149–152. doi:10.2307/2796709. JSTOR 2796709.
- ^ «Carrying a Wolf, a Goat, and a Cabbage across the Stream. Metamorphoses of ATU 1579», Piret Voolaid, Folklore: Electronic Journal of Folklore 35 (2007), pp. 111–130. Tartu: Eesti Kirjandusmuuseum.
- ^ p. 17, Rediscovered Lewis Carroll Puzzles, Lewis Carroll, compiled by Edward Wakeling, Courier Dover Publications, 1996, ISBN 0-486-28861-7.
- ^ «Springfield! Springfield!».
External links[edit]
- Goat, Cabbage and Wolf A Javascript simulation
- Fox, Chook and Corn A simulation without Javascript needed
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
‹
›
Я увлекаюсь занимательными вопросами, задачами
и головоломками, в свободное время собираю коллекцию по этой теме и с интересом
слежу за рубриками «Психологический практикум» и «Математические досуги».
В разные годы у нас было издано немало
книг в этом жанре, а в Петербургской публичной библиотеке удается разыскать
головоломки прошлых лет и даже веков.
Работая со своей коллекцией, я обратил
внимание, что многие головоломки, известные с незапамятных времен, кочуют
из книги в книгу разных авторов, обрастая новыми красочными деталями и
подробностями и приобретая тот неповторимый стиль и колорит, которые отличают
больших мастеров этого жанра.
Так, читая книгу Сэма Лойда, обращаешь
внимание на веселое хвастовство и откровенный рекламный характер головоломок
этого американского патриарха занимательной математики.
Генри Дьюдени свои задачи изящно стилизует
под средневековье, чем, несомненно, повышает читательский интерес.
Льюис Кэрролл неистощим на придумывание
«лепых нелепиц», продолжая традицию «Алисы в стране чудес».
Свои связи и контакты с читателями любит
подробно описывать Мартин Гарднер, демонстрируя умение не отставать от
прогресса науки.
К сожалению, гораздо меньше «головоломщиков»
у нас в России. Но мы можем гордиться знаменитым «доктором занимательных
наук» Я. И. Перельманом, обладавшим талантом видеть необычное в обычном
и из самого незамысловатого факта сделать «конфетку».
Много изданий выдержала книга Б. А. Кордемского,
который старался придать головоломкам дидактический характер и наполнить
известные классические задачи на математическую смекалку современным содержанием
(см. «Наука и жизнь» № 6, 1964 г.; № 12, 1995 г.; №№ 4, 9, 10, 11, 12,
1996 г.).
Нельзя не упомянуть и книгу П. В. Маковецкого,
увязывающего современные научные достижения с творчеством Козьмы Пруткова
(см. «Наука и жизнь» №№ 7-12, 1966 г.; №№ 1-5, 9, 1967 г.; № 2, 1968 г.).
Постепенно у меня появилась идея: спародировать
стиль и литературные приемы упомянутых авторов, что я и попытался сделать
в меру своих способностей. Известен нехитрый прием: берется некое широко
известное произведение и далее представляется, как тот или иной автор
написал бы на эту тему. Я взял за основу старинную
русскую головоломку о том, как крестьянин должен был перевезти через реку
в двухместной лодке волка, козу и капусту. А как бы на эту тему написали
мастера головоломок?
ЗАДАЧА, ПРИДУМАННАЯ В ПОЛНОЧЬ
Три, уф! — звучит почти
как триумф, с. 25.
Льюис Кэррол.
История с узелками. М.: Мир,
1985.
Уже появились угрюмые ночные тени, когда пятеро
усталых путников подошли к побережью.
— Вы хотите сесть на наш Грурмстипс? —
спросил капитан, — для этого нужно разрешение Ее Блистательства. Между
нами: в часы бессонницы она обожает решать головоломки.
— Кто вы и куда направляетесь? — спросила
Ее Блистательство.
— Меня зовут Бальбус, — сказал старший
из них, — в честь героя одной книги — сборника упражнений по латинскому
языку. Моих племянников зовут Хью и Ламберт. Направляемся мы на родину
в Кговжднию. Пожалуйста, возьмите нас на Грурм… на ваш корабль.
— Ваше Лучезарное Сверкательство! — воскликнул
Хью, — вот прекрасная головоломка. Год назад мы покинули страну, имея лишь
1000 фунтов стерлингов. В Лондоне мы рассчитывали разбогатеть, но сначала
нам не везло. Зато сегодня мы, как никогда, близки к целому миллиону! Каким
образом?
— Меня зовут Безумная Математильда, — сказала
женщина, — я не умею жарить омлет. А это моя племянница Клара.
— Ваше Многозвездное Всесокрушительство,
— сказала Клара, — мы будем всю дорогу для вас считать встречные корабли.
Я это будут делать так: один, уф! Два, уф! Три, уф!
— Это звучит почти как триумф, — заметила
Ее Блистательство, — хорошо, мы отвезем вас в Кгов… на вашу родину. Приходите
сегодня обедать к капитану, будет много народа. Капитан пригласил отца
своего сына и племянника своего дяди, внука своего дедушки и брата своей
сестры, сына своей матери и мужа своей жены. Надеюсь, вы сумеете
подсчитать количество гостей? Капитан! Отведите путников под ДУШ, пусть
они отмоют свои пыльные ДУШИ.
Ответы и решения
Ответ на первую головоломку: чтобы заполучить
миллион, Бальбус с племянниками решили ограбить Лондонский банк.
Разумеется, это шутка. Я полагаю, что шутки
вполне уместны в книге, призванной не поучать, а развлекать.
Ответ на вторую головоломку о гостях капитана
я привести не могу, так как не знаю, как ее решить.
ЧИСЛОВЫЕ ВЕЛИКАНЫ ВНУТРИ И ВОКРУГ НАС
Масса нашего солнца в
граммах равна
1 983 000 000 000 000 000 000 000 000 000 000
Я. И. Перельман. Занимательная
алгебра. М.: Наука, 1975, с. 9.
Числовые великаны находятся внутри и вокруг
нас. Это как нельзя лучше иллюстрирует русская головоломка о крестьянине,
волке, козе и капусте. Знаете ли вы, сколько съедает крестьянин за всю
жизнь? Сколько выпивает молока и кваса, выхлебывает щей и съедает каши?
Сколько ему надо мяса и рыбы, картофеля и яиц, не говоря уже о кофе и коньяке?
По моим подсчетам для этого потребуется длинный товарный поезд весом около
1 000 000 000 граммов.
Интересный числовой великан связан с волком.
Преследуя добычу, серый хищник может в сутки пробежать более 65 км, что
составит за год 23790 км, за 15 лет жизни он может пробежать 356850 км,
а если перевести это число в миллиметры, то получится расстояние от Земли
до Луны! Недаром говорят в народе: «Волка ноги кормят»!
Любопытная головоломка связана с козой.
Известно, что козья шерсть — лучшее сырье для пуховых платков. А задумывались
ли вы над тем, есть ли на земле две козы с одинаковым числом волос? Давайте
прикинем вместе. На одном квадратном сантиметре кожи козы растет примерно
1000 волос. Если представить себе тело козы в виде параллелепипеда с размерами
20ґ30ґ50 см, то площадь, занятая волосами, будет равна 6200 см2,
и тогда на козе имеется 6200000 волосинок. А сколько в мире коз? Пусть
в среднем имеется одна коза на 1000 жителей, тогда на 5000000000 жителей
Земли приходится 5000000 коз. Это значит, что двух коз с одинаковым числом
волос может и не найтись, а жаль.
Еще более интересный числовой великан связан
с капустой.
Как известно, игральные карты были впервые
придуманы в России думским дьяком Степаном Бутлером. Царю Ивану Грозному
очень понравилась новая игра, и он пообещал щедро наградить изобретателя,
выполнив любую его просьбу. Степан же Бутлер, любивший закусывать квашеной
капустой, попросил выдать ему столько кочанов капусты, сколько получится,
если на первую карту положить один кочан, на вторую — два, на третью —
четыре, на четвертую — восемь и так на каждую следующую карту вдвое больше,
чем на предыдущую, до последней 36-й карты.
Когда царский математик подсчитал размеры
награды, то оказалось, что думскому дьяку надо выдать 236
— 1 = 68719476735 кочанов! Такое количество капусты невозможно было вырастить
на скромной площади тогдашней России, а поскольку Иван Грозный любил держать
данное им слово, то немедленно принялся расширять пределы царства. Это
и явилось истинной причиной завоевания Казанского и Астраханского ханств.
РАССКАЗ ПИОНЕРА
Летом во время похода
два пионерских звена собирали лекарственные травы,
с.189
У учительницы одной из
начальных школ штата Нью-Йорк пропал кошелек,
там же.
Б. А. Кордемский. Математическая
смекалка. М.: Физматгиз, 1958.
Заканчивались школьные каникулы, и мы покидали
гостеприимный лагерь Артек. После утренней линейки три пионерских отряда
были готовы к отъезду, но автобус пришел только один, и сесть в него мог
только один отряд.
Возник спор.
— Наш отряд должен ехать первым, мы все
время собирали лекарственные травы и сдавали в аптекоуправление, — сказал
Володя Лавров, — причем пионеры первого звена собрали трав вдвое больше,
чем второго, а третьего — столько, сколько все три вместе взятые.
— Нет, этот автобус наш, — заявила Нурия
Сараджева, которая одной из первых начала применять способ сборки хлопка,
как известная Мамлакат, — и мы трудились все лето, заготавливая дрова на
зиму для своей школы. Недаром мне в Артеке подарили этот прямоугольный
коврик, который я дома должна переделать в квадратный.
— Но нам надо срочно ехать, — попросил
Коля Синичкин, — наш отряд им. Павлика Морозова должен успеть к пуску межрайонной
гидроэлектростанции, построенной комсомольцами в неурочное время. Нам поручено
украсить здание флагами, да еще как: 12 флагов надо расположить на четырех
сторонах здания по пять с каждой стороны.
Подошел старший пионервожатый.
— Друзья, — сказал он, — сделаем так: я
задам вам головоломку, и какой отряд ее решит первым, тот и поедет первым.
Итак, слушайте.
У учительницы одной из начальных школ штата
Нью-Йорк пропал кошелек. Украсть кошелек мог кто-то из пяти учеников: Лилиан,
Джуди, Дэвид, Тео или Маргарет. При опросе детей каждый из них сказал:
Лилиан: я не брала кошелек. Мы с Джуди
курили в коридоре.
Дэвид: а мы с Тео пили виски на чердаке.
Это, наверное, Джуди.
Маргарет: Дэвид и Тео на перемене грабили
ларек у школы, а я стерегла учительскую. Кошелек учительница просто потеряла.
При дальнейшем распрашивании каждый признался,
что из сделанных им заявлений первое — верное, а второе — нет. Кто взял
кошелек?
Первым нашел решение второй отряд, который
и сел в автобус.
К сожалению, радость ребят была омрачена:
в поезде Симферополь — Москва у Нурии Сараджевой пропал подаренный ей в
Артеке коврик.
И неудивительно: в соседнем купе ехали
американские туристы.
КАК СЭКОНОМИТЬ МОЗГИ ЧИТАТЕЛЕЙ?
Научная статья пишется
кратко… Правда, при этом экономится бумага,
но упускается из виду,
что экономить следовало бы не бумагу, а мозги читателей, с. 413.
Для недогадливых: автор
шутит, с. 66.
П. В. Маковецкий. Смотри
в корень! Сборник любопытных задач и вопросов. М.: Наука, 1976.
Часть А
Вы находитесь в космическом корабле на
орбите спутника Земли с волком, козой и капустой и вам предстоит приземление.
Вы собираетесь развернуть корабль с помощью двигателей ориентации, но они
неожиданно отказали. Как быть?
Часть Б
Щелкни кобылу в нос —
она махнет хвостом.
Козьма Прутков. Мысли и афоризмы,
№ 58.
Обращаю внимание кибернетиков на то, что высказывание
Пруткова является первой в мировой литературе и предельно четкой формулировкой
проблемы «черного ящика», а также первым в этой области результатом эксперимента*.
Часть В
В части Б я намекнул, что для решения задачи
надо использовать хвост. Действительно, для поворота корабля надо заставить
волка и козу вращать хвостами. Заменим для простоты расчетов корабль тонкостенным
цилиндром, имеющим радиус r
= 1 м и массу m = 106
г, а хвосты волка и козы соответственно цилиндрами радиусами 1 см и 0,5
см и массами 500 г и 100 г.
Тогда на основе закона сохранения количества
движения
мы получим соотношение угловых скоростей
То есть для того, чтобы развернуть корабль
на 180о, вашим двум животным придется, делая 1 об/с хвостами,
трудиться два месяца, после чего корабль и займет нужное для приземления
положение.
За это время вы можете выйти в открытый
космос для ремонта, захватив с собой капусту. Если вы нечаянно оторветесь
от корабля, быстро бросайте кочан в противоположную сторону. И если он
весит 2 кг, а вы — 100 кг, то скорости броска в 50 м/с достаточно, чтобы
причалить к кораблю.
Правда, вернувшись на землю, вы получите
крупную нахлобучку за засорение космоса и к тому же останетесь без салата.
Но что хуже?*
* Для недогадливых: автор шутит.
НЕТРАНЗИТИВНЫЙ ПАРАДОКС
Фотокопию этой редкой
книги любезно прислал мне
Сигео Такаги, фокусникиз
Токио, с. 64.
Однако нетрудно привести
примеры отношений,
которые нетранзитивны,с.
67.
Мартин Гарднер. Путешествие
во времени. М.: Мир, 1990.
В журнале Scientific American я опубликовал
старинную китайскую головоломку из редкой книги Сей Шонагон, фотокопию
которой мне любезно прислал Янь Инь, фокусник из Пекина. В ней шла речь
о китайском мандарине, переправлявшемся на джонке через реку Хуанхэ с дочерью,
тигром и козой.
Хотя ответ очевиден, впервые он был явно
сформулирован А. Дэвисом из Нортбрука в 1916 году. Профессор английского
языка Рейс сообщил, что это была любимая головоломка Наполеона, а датский
студент-физик из университета Брандейса прислал изящное доказательство
того, что тигра и девушку нельзя перевозить вместе, даже в присутствии
отца.
Я хочу поблагодарить математика В. Милли,
приславшего нерекуррентную формулу решения задачи, а также признателен
Риду из Сан-Кристобаля за правило, согласно которому путь джонки должен
быть топологически эквивалентным, т. е. не иметь самопересечений.
Многие заметили, что сюжет этой головоломки
изображен на купюре достоинством в 1 доллар.
Свой рассказ об этой удивительной головоломке
я хочу закончить двумя жемчужинами мудрости: «Прошлое находится впереди
нас, будущее — позади».
Дополнение
Когда эти заметки были уже готовы, пришло
еще два письма.
В первом В. Хакен из Висконсинского университета
напомнил, что у козы было семеро козлят. Это существенно усложняет задачу.
Ему удалось составить программу и запустить в микрокомпьютер, который после
получаса работы выдал результат: решений оказалось 951. Компьютер был присоединен
к графопостроителю, который вычертил траектории движения джонки.
Второе письмо оказалось от общества защиты
животных из Китая. В нем был изложен протест против публикации этой головоломки:
О, мистер Гарднер, только янки
способен отпустить в грозу
На джонке дочку китаянки и с ней
несчастную козу…
Общество защиты животных предъявило мне
иск на 40 млн. долларов.
В связи с этим сообщаю, что публикация
данной головоломки не что иное, как первоапрельская шутка.
ВЕЛИКИЙ ДИСПУТ МЕЖДУ ПЕРЕВОЗЧИКОМ И ПРИСТАВОМ ЦЕРКОВНОГО СУДА
На поле он стоял и думал:
козлу дорога далека, с. 14.
— Клянусь небом, — воскликнул
Пристав, — ты сущий болван! с. 49.
Генри Э. Дьюдени. Кентерберийские
головоломки. М.: Мир, 1979.
Случилось так, что компания паломников отдыхала
в старой харчевне «Табард» у реки, и трактирщик предложил им скоротать
дорожную скуку, рассказывая по очереди головоломки.
— Я перевозчик, — сказал один из завсегдатаев,
чья очередь подошла занимать гостей, — у меня есть маленькая лодка с одним
местом для пассажира. Так что если кому понадобится переправиться на другой
берег — милости просим, один фартинг за перевоз. В тот день, о котором
я вам расскажу, на берегу меня ждали:
Брат Келарь с бочкой пива, которую он вез в монастырь, Славный Рыцарь,
вернувшийся из крестового похода с красавицей турчанкой, и, вооруженный
удочками, Йомен, сидевший сутками на берегу. И всем надо на другую сторону.
Я уже мысленно подсчитывал выручку, но
случилось непредвиденное. Вдруг Брат Келарь сказал: «Хоть у тебя всего
лишь одно место, я со своей бочкой не расстанусь!»
Славный Рыцарь тоже не согласен сесть в
лодку без спутницы. Словом, плакали мои денежки.
И все же я заработал свои три фартинга,
но как?
— Клянусь пером и чернильницей, — воскликнул
Оксфордский Студент, — я бы не растерялся и попросту взял красотку на руки!
— Так я и получил первый фартинг, а второй?
— Какое пиво было в бочке? — спросил Монах,
«что рожей красен был как рак и, видно, выпить не дурак».
— Настоящий лондонский эль.
— Клянусь костями Святого Джинго, раз Келарь
не хотел расстаться с бочкой, то мог расстаться с элем! Я бы предложил
распить славный напиток, а Келаря посадить в бочку, вот он с ней и не расстанется!
— А третий фартинг заплатил Йомен, — догадалась
Братская Ткачиха.
Вся компания похвалила головоломку Перевозчика,
но Пристав Церковного Суда спросил:
— А что вы сделали с утками? Зажарили и
съели?
— С какими утками? — удивился Перевозчик.
— Ты же сказал, что у рыбака были утки!
— Да ничего подобного я не говорил!
— Клянусь небом, — воскликнул Пристав,
— ты сущий болван!
Великий Диспут между Приставом и Перевозчиком
закончился только после того, как Перевозчик объяснил, что…
Впрочем, читатель уже сам, наверное, догадался,
в чем дело.
ГОЛОВОЛОМКА ГУБЕРНАТОРА
Люди буквально помешались
на этой головоломке, с. 30.
Более 50000 читателей написали в редакцию, с. 76.
Сэм Лойд. Математическая
мозаика. М.: Мир, 1984.
Много лет назад, когда я возвратился из Европы
вместе с Эндрю Г. Кертином, военным губернатором штата Пенсильвания, мы
любовались красивой фермой, построенной в форме лошади.
— Эта ферма принадлежит славным супругам
О’Тул, — сказал губернатор, — они познакомились на этом самом месте во
время колонизации Америки. Разговор закончился довольно неожиданно:
— Лойд, а не повод ли это для головоломки?
Было не слишком сложно, трясясь на муле,
внести улучшения в отдельные части его рассказа. Вот что получилось.
Однажды молодой ковбой повстречал на дороге
юную молочницу, которая вела за собой корову, а сзади бежала собака. Он
соскочил с коня и подошел к девушке, которая вдруг испуганно вскрикнула.
— Ты чего? — спросил ковбой.
— Так ты же хочешь поцеловать меня против
моей воли, — ответила скромница.
— Как бы я смог это сделать? В одной руке
у меня ружье, в другой — повод коня.
— А что мешает тебе воткнуть ружье в землю
и привязать к нему коня? — спросила тихоня.
— Да твоя корова косится на меня и в это
время непременно боднет, — оправдывался ковбой, — а собака укусит мою лошадь.
— О, эта глупая собака не кусается, а корову
ты можешь выгнать на пастбище, — не унималась недотрога…
Подскажите, что делать бедному ковбою,
да поскорее, потому что Гарри и Джейн вот-вот заведут общее хозяйство.
Старожилы помнят, как я свел с ума весь
мир этой головоломкой. Психиатрические больницы были переполнены. Бродяги
забывали пить свой утренний кофе, а продавцы — давать сдачу. Приз в 10000
долларов, предлагавшийся за первое правильное решение, так никому и не
был присужден.
Либерально-республиканская партия предложила
мне баллотироваться в президенты.
Да… Мир меняется стремительно, и любители
головоломок стали куда более проницательными, чем прежде.
И все-таки предложите своим друзьям эту
головоломку, чтобы позабавиться их смущением.
Презентация на тему: » Разработка плана действий и его запись. Волк, коза и капуста Задача: Мальчик лодочник должен перевезти на противоположный берег реки волка, козу и капусту.» — Транскрипт:
1
Разработка плана действий и его запись
2
Волк, коза и капуста Задача: Мальчик лодочник должен перевезти на противоположный берег реки волка, козу и капусту. При перевозке необходимо учесть, что с собой в лодку можно взять либо волка, либо козу, либо капусту, и при этом нельзя позволить волку съесть козу, а козе – капусту. Как это сделать?
3
Волк, коза и капуста Возможные действия мальчика: Переправиться одному Перевезти козу Перевести волка Перевезти капусту
4
Волк, коза и капуста Правильная последовательность действий: 1.Перевезти козу 2.Переправиться одному 3.Перевезти капусту 4.Перевезти козу 5.Перевести волка 6.Переправиться одному 7.Перевести козу
5
Решение в виде таблицы Шаг На этом берегу Кто в лодке Куда На том берегу 1В, КПМ, К 2В, КПМК 3ВМ, КПК 4ВМ, ККП 5КМ, ВКП 6КМВ, КП 7М, КВ, КП Обозначим: М – мальчик, В – волк, К – коза, КП – капуста
6
Решение в виде схемы Обозначим: – мальчик, – волк, – коза, – капуста
Логические игры и головоломки — это отличное развлечение как для детей, так и для взрослых. Они вырабатывают привычку думать, рассуждать, делать выводы и всегда стараться найти решение проблемы.
Задачка про волка, козу и капусту
Помните старинную задачу про волка, козу и капусту? Кто не решал ее в детстве! Предложите задачу своему ребенку! Мужику нужно перевезти через реку волка, козу и капусту. Но в лодке может поместиться только он сам, а с ним или только волк, или только коза, или только капуста. Но если оставить волка с козой, то волк съест козу, а если оставить козу с капустой, то коза съест капусту. Как мужику перевезти свой груз?
Решение:
Нужно начать с козы. Перевезя ее, мужик возвращается на другой берег и берет волка. Переправив волка, он оставляет его на другом берегу, но зато берет козу и везет ее обратно на первый берег. Здесь он оставляет ее и перевозит к волку капусту. Затем, вернувшись, берет козу — переправа благополучно заканчивается.
Детективная задачка
На лугу лежат пять кусочков угля, одна морковь и шарф. Никто не клал их туда. Почему они там лежат?
Решение:
Дети использовали эти предметы, когда лепили снеговика зимой. С приходом весны снеговик растаял, и пять кусочков угля, морковка и шарф остались лежать уже на лугу.
Летная задачка
Мужчина выпрыгивает без парашюта из самолета. Высадка небезопасная, но мужчина остается целым и невредимым. Почему?
Решение:
Самолет находится ещё на взлётно-посадочной полосе.
Задачка про ноги
Ваня идет к лесному озеру. Ему навстречу движется класс из 25 учеников и двух преподавателей. Родители 10 детей также принимают участие в прогулке. Пять матерей еще везут своих детей на колясках. Преподаватель ведет с собой собаку. Сколько ног идут по дороге к лесному озеру?
Решение:
По дороге к лесному озеру идут только две ноги — Ванины. Все, кого он встретил, возвращаются с озера.
Сколько ворон?
Вишня у Маши плодоносит в большом количестве. К сожалению, на дерево садятся вороны и безжалостно клюют плоды. Вечером Маша считает ворон. Их 38! Это настолько выводит ее из себя, что она ловит одну ворону сачком. Сколько ворон осталось на дереве?
Решение:
Осталась только одна ворона, пойманная Машей. Остальные вороны испугались и улетели.
Задачка на внимательность
Молодая девушка заказывает в кафе яблочный сок, рулет и шоколадное мороженое. Официант, который принимает заказ, приносит ей вскоре все желаемое. После того как девушка оплатила заказ, официант спросил: «Трудно работать в полиции?» Как он догадался, что девушка — полицейский?
Решение:
Девушка была в полицейской форме.
День рождения князя
Когда князь празднует день рождения, его подданные должны принести ему достойный подарок: самую сочную ветчину, самый пряный сыр, самую упитанную курицу, искусно выделанные шкурки, плетеные корзинки, глиняные кувшины и резные изделия. Крестьянин сделал князю необычный подарок: бутылку с яблочным соком. Отличие этого подарка — яблоко находится в бутылке. Князь поражен: каким образом тот смог засунуть яблоко в бутылку? «Как ты сделал это? При помощи колдовства?» — спрашивает князь. Крестьянин отвечает: «Догадайтесь сами, но я вовсе не чародей!» Как яблоко попадает в бутылку?
Решение:
Крестьянин надевает бутылку на яблоневую ветку вскоре после цветения. Таким образом, плод развивается в бутылке.
Еще один вид логических игр придется всем по вкусу — это игры с палочками. Для игры понадобится набор счетных палочек или любые палочки одинаковой длины и толщины (например, спички, с которых предварительно счистили серу), подойдут и полоски картона. Если вы играете вместе с детьми, то можно давать устные задания. Если ребенок играет один, подготовьте карточки с рисунком и условием игровой задачи.
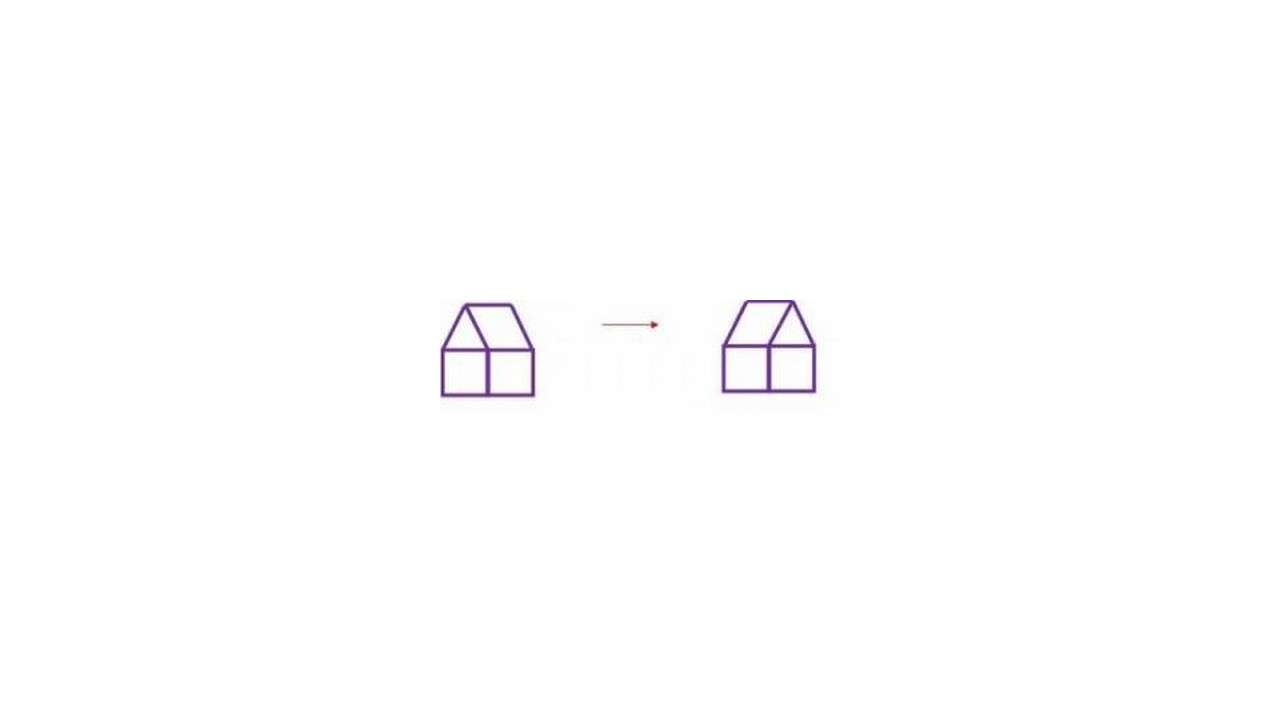
Задание № 1
Переложи одну палочку так, чтобы дом смотрел в другую сторону.
Задание № 2
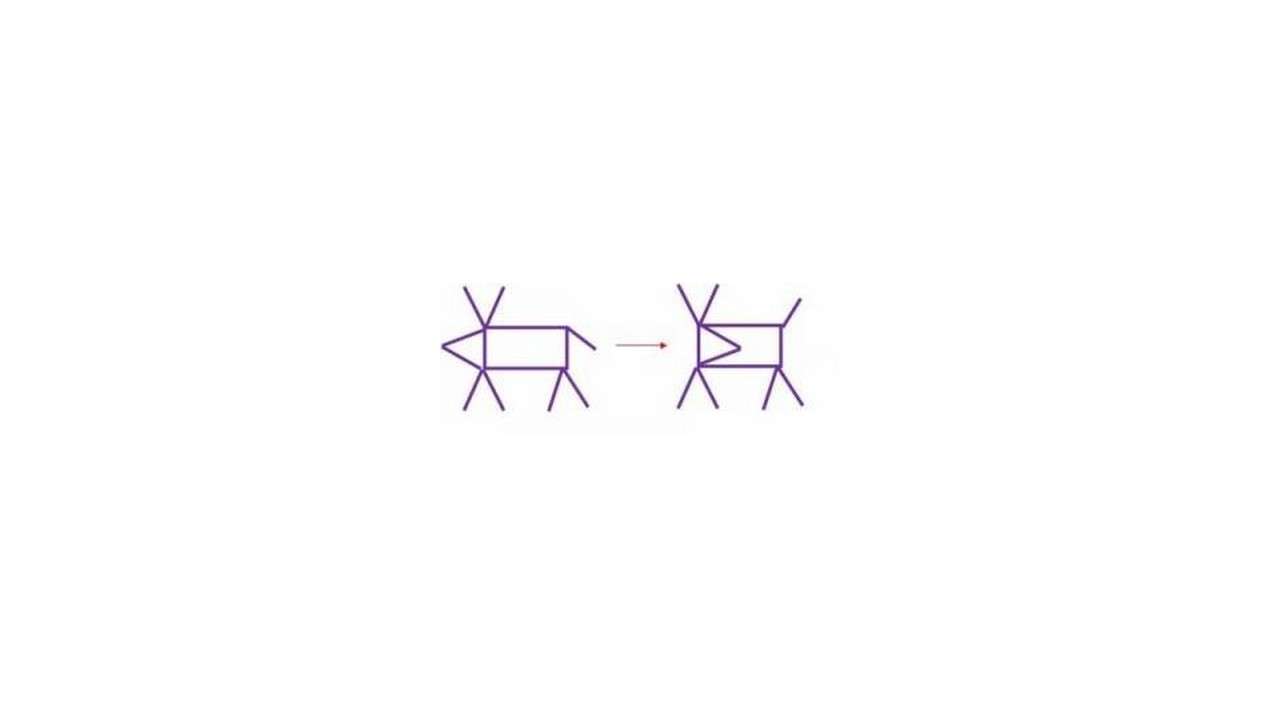
Переложи 3 палочки так, чтобы корова оглянулась и подняла хвост.
Еще несколько заданий с палочками из пособия С. И. Волковой «Математика и конструирование» (1−4 классы):
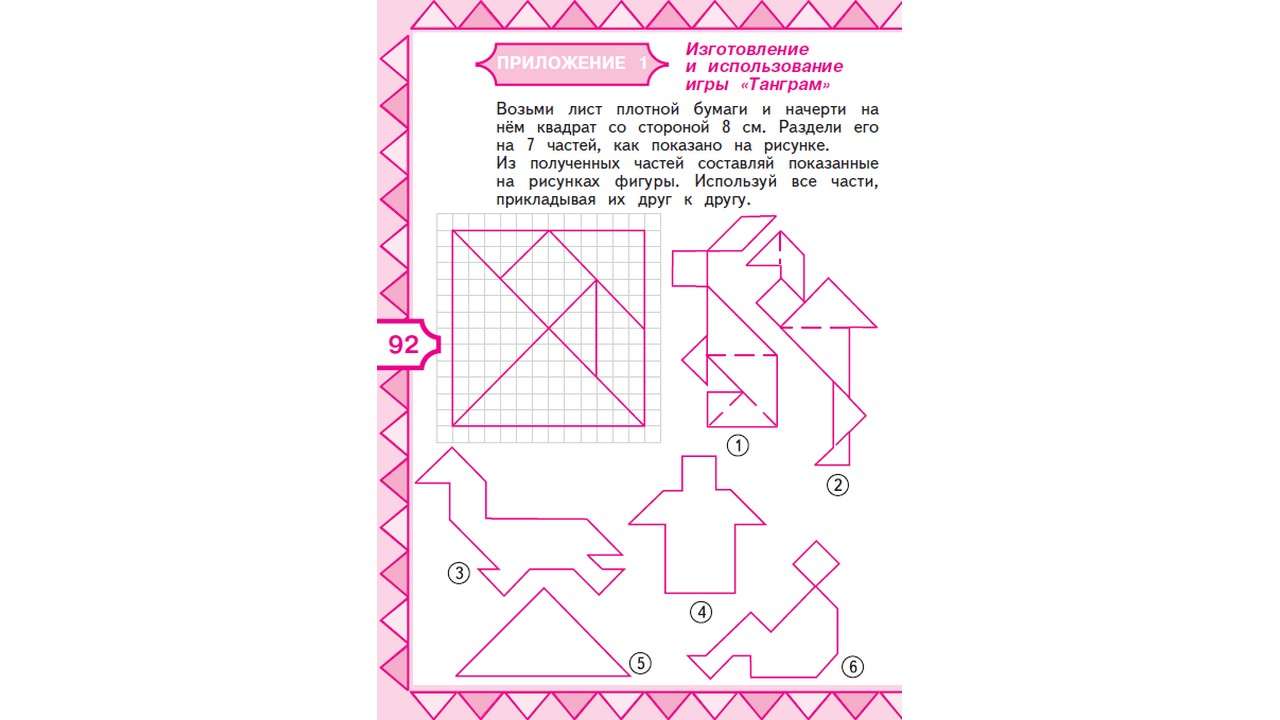
А в завершении мы хотим предложить вам самостоятельно изготовить знаменитую китайскую головоломку «Танграм». И в этом нам опять поможет пособие С. И. Волковой «Математика и конструирование».
Из деталей этой головоломки можно складывать разные фигуры. Сложите для начала 1 и 2 фигуры. Рисунок вам поможет. Теперь попробуйте сложить фигуры 3, 4, 5, 6. И с этим справились? Поздравляем!
Надеемся, что выполняя предложенные задания, вы и ваш ребенок не раз испытали радость от приложенных интеллектуальных усилий, а главное — от самостоятельно найденного решения.
Фото: NadyaEugene/masterone/Shutterstock.com, архив пресс-службы,